Rovnica roviny
1. Akým spôsobom je v priestore určená rovina?
Riešenie:
Rovina v priestore je určená tromi rôznymi bodmi A,B,C, ktoré neležia na jednej priamke.

2.Napíšte všeobecnú rovnicu roviny, v ktorej leží bod A [-1;5;0]. Prechádza rovina ρ počiatkom súradníc? Normálový vektor roviny je
Riešenie:
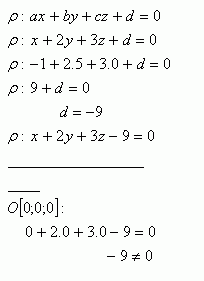
Rovina x +2y +3z -9 = 0 neprechádza počiatkom súradníc.
3. V rovine ρ ležia tri body A[2 ; -4; 5], B[3; -1;4], C[0; -10; 7]. Napíšte parametrické vyjadrenie tejto roviny.
Riešenie:
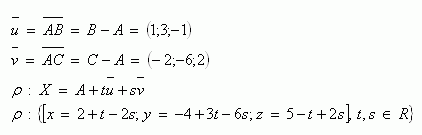
4.Rovina ρ je daná parametrickými rovnicami. Prepíšte ich do všeobecnej rovnice roviny.
Riešenie:
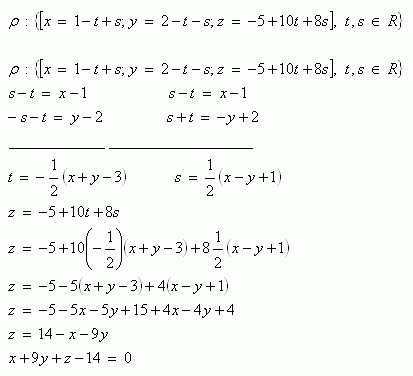
Rovnica roviny vo všeobecnom tvare je ρ: x + 9y +z -14 = 0
5. Napíšte rovnicu roviny σ, ktorá prechádza bodom A [3;4;-5] a je rovnobežná s vektormi
Riešenie:

6.Napíšte rovnicu roviny, ktorá prechádza bodmi A [2;-4;5], B [3;-1;4], C [0;1;6]
Riešenie:

Rovnica roviny je 8x + y + 11z – 67 = 0
7. Napíšte rovnicu roviny, ktorá je daná dvoma rovnobežnými priamkami:
Riešenie:

Rovnica roviny je ρ: 2x + y -1 = 0
8.Napíšte všeobecnú rovnicu roviny τ , ktorá je rovnobežná s osou x a prechádza bodmi A[-2;-1;-3], B [2;3;0]
Riešenie:

Rovnica roviny je τ: 3y – 4z -9 =0
9. Napíšte rovnicu roviny π , ktorá prechádza bodom M[-4;0;4] a vytína na súradnicových osiach úseky p = 4, q = 3.
Riešenie:
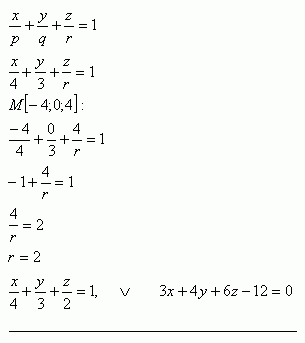
Rovnica roviny π: 3x +4y +6z -12 =0
10. Daná je rovina ρ : 2x -2y +z -6 = 0. Vypočítajte uhly jej normály so súradnicovými osami x, y, z.
Riešenie:
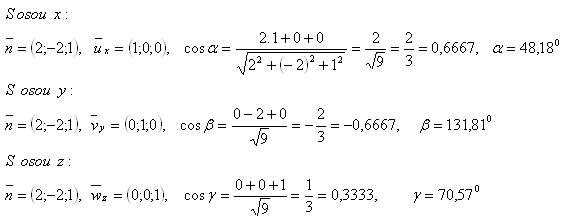
Uhly normály so súradnicovými osami sú: α = 48,180,β= 131,810,γ= 70,570
11.Zistite či bod A [22;2;–5] leží v rovine
Riešenie:

Bod A leží v rovine ρ.
12.Určite súradnicu „x“ bodu M [x;1,2], aby bod M ležal v rovine
Riešenie:
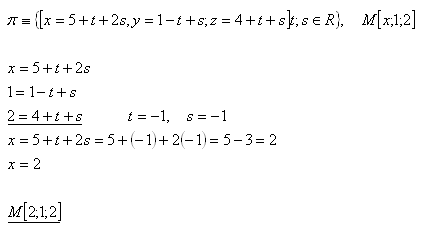
Hľadaná súradnica bodu M je x = 2. Bod M [2;1;2].
13.Napíšte všeobecnú rovnicu roviny, ktorá prechádza bodom A a je kolmá na úsečku AB, ak platí:
Riešenie:
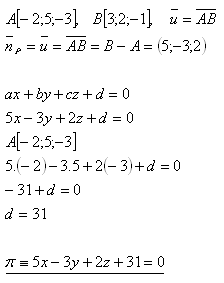
Rovnica roviny je π : 5x - 3y + 2z + 31 = 0
14.Napíšte všeobecnú rovnicu roviny τ, ktorá vytína na súradnicových osiach úseky p = 2, q = 1, r = 5.
Riešenie:
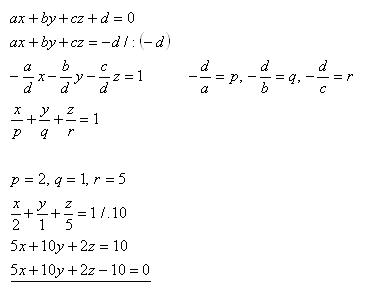
Rovnica roviny je τ : 5x + 10y +2z – 10 = 0
15.Napíšte rovnicu roviny π, ktorá prechádza bodom M a je kolmá na priamku p. Riešte pre zadanie:
Riešenie:
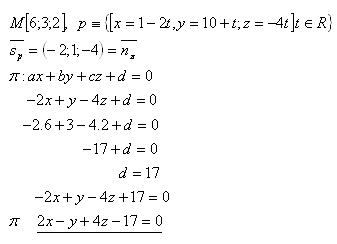
Rovnica roviny je π : 2x – y + 4z – 17=0
16.Ukážte, že body A,B,C,D ležia v jednej rovine. Riešte pre:
Riešenie:
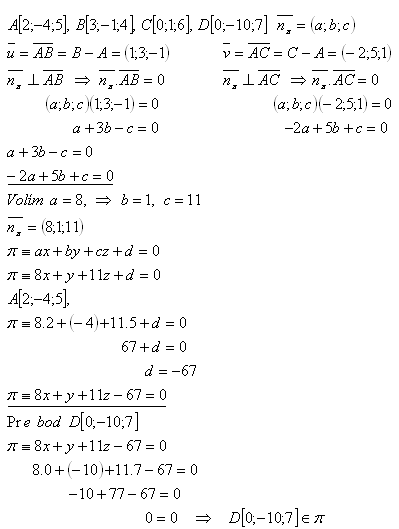
Bod D[0;-10;7] leží v rovine π. Všetky body A,B,C,D ležia v rovine π.
17.Dané sú tri guľové plochy π, τ, ρ. Napíšte všeobecnú rovnicu roviny χ, ktorá prechádza stredmi týchto guľových plôch. Platí:
Riešenie:
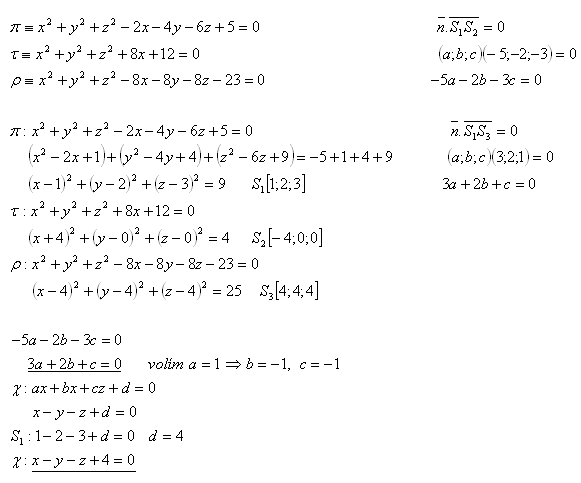
Rovnica roviny je: x – y – z +4 = 0
18.Napíšte všeobecnú rovnicu roviny π, ktorá prechádza bodmi
Riešenie:
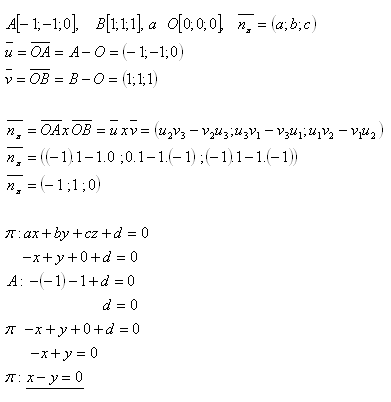
Rovnica roviny je π : x – y = 0
19.Prepíšte parametrický tvar roviny μ na všeobecný, ak platí
Riešenie:
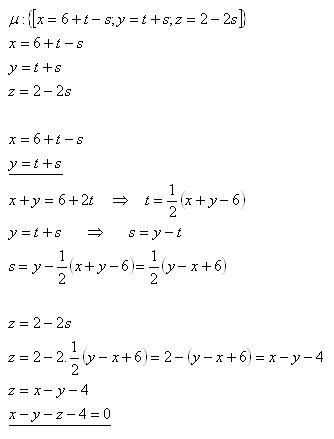
Rovnica roviny μ vo všeobecnom tvare je μ: x – y –z – 4 = 0
20.Pre ktorú hodnotu parametra „m“ z množiny R leží bod M[0;6;m] v rovine
Riešenie:
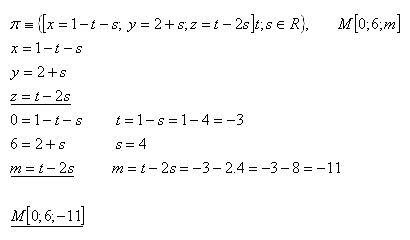
Parameter „m“ je m = –11. Bod M [0;6;-11].