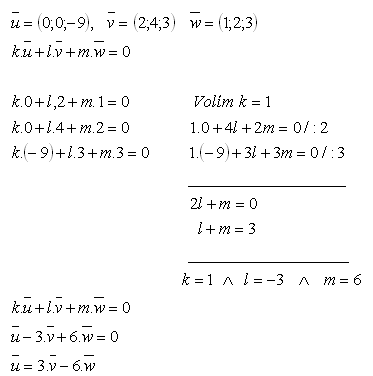Vektor v priestore
1. Aké sú vlastnosti vektora v priestore.
Riešenie:

2.Zistite dĺžku úsečky AB, ktorá má stred S v počiatku súradnicových osí a bod A [6; -2; 3]
Riešenie:

3.Určite súradnice vrcholu C [c1; c2; c3] v trojuholníku Δ ABC, ak vrcholy a ťažisko majú polohu: A [3;3;3], B [-2;1;2], T [0;-1;0]. Zistite tiež obvod tohto trojuholníka.
Riešenie:
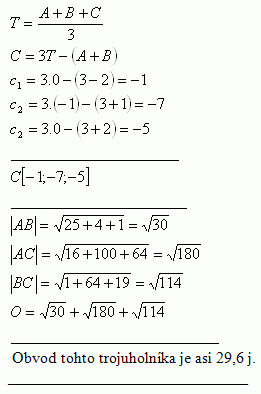
4.Na osi z nájdite bod, ktorý je rovnako vzdialený od bodov A [ -2;1;4] a B [3;0;1]
Riešenie:

5. V rovnobežnostene ABCDEFGH sú známe súradnice bodov A[2;-3;1], B[3;-4;2], D[4;2;-3], E[5;3;4]. Vypočítajte súradnice zvyšných bodov C, F, H, G
Riešenie:
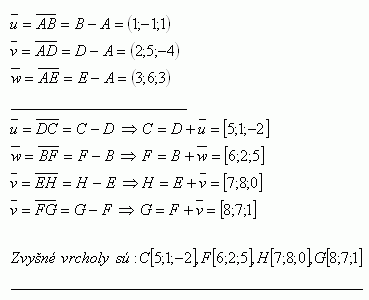
6.Dokážte, že trojuholník Δ ABC je rovnoramenný a pravouhlý ak: A[2;-4;9], B[-1;-4;5], C[6;-4;6]
Riešenie:
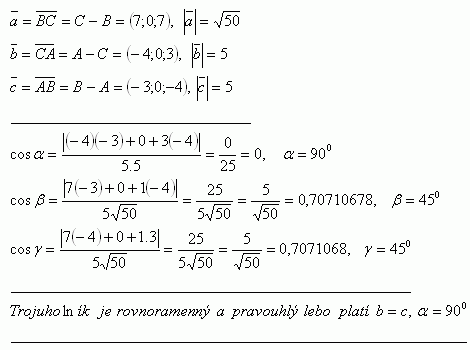
7.Dané sú vektory:
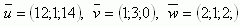
Zistite, či sú lineárne závislé.
Riešenie:

8.Zistite, či dané štyri body ležia v jednej rovine. A[1;2;-1], B[0;1;5], C[-1;2;1], D[2;1;3]
Riešenie:

9.Vypočítajte obsah trojuholníka Δ ABC, ktorého vrcholy ležia v bodoch:
Riešenie:

10.Vypočítajte objem štvorbokého ihlana ABCDV, ak poznáte jeho vrcholy: A[2;0;0], B[0;3;0], D[0;0;6], V[2;3;8]
Riešenie:

11. Určite dĺžku ťažnice v trojuholníku ABC, ak platí A[1;0;2], B[-2;1;-3], C[0;-1;1].
Riešenie:
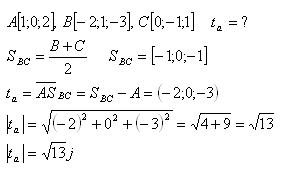
12. Určite vzdialenosť stredov úsečiek AB, CD ak platí:
Riešenie:
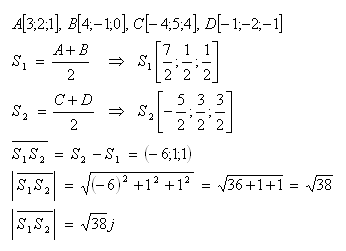
13.Nech A[1;2;8] a B[4;y;4], potom |AB| = 5. Aké bude y?
Riešenie:

Hľadaný bod je B[4;2;4].
14. Dané sú body K, L, M, N. Vypočítajte súradnice bodu N ak platí:
Riešenie:
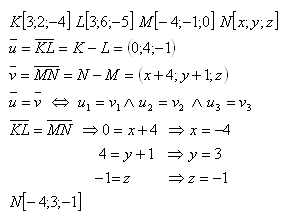
Hľadaný bod je N [-4;3;-1].
15.Dané sú body A[4;-3;2], B[5;0;-1]. Určite čísla m, n tak, aby bod C[2;m;n] ležal na vektore AB.
Riešenie:
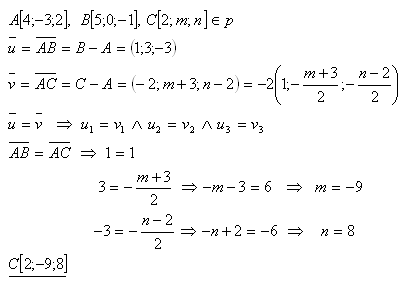
Hľadaný bod je C[2;-9;8].
16.Určite vzájomnú polohu vektorov
Riešenie:
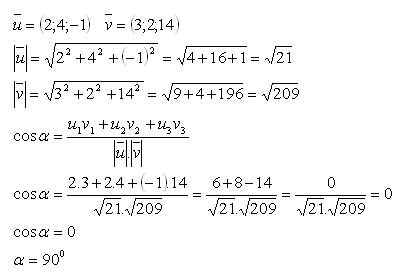
Dané vektory sú na seba kolmé.
17. Dané sú tri body v priestore A, B, C. Vypočítajte veľkosť uhla
Riešenie:
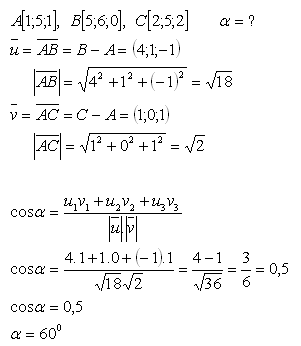
Uhol medzi vektormi je α = 600.
18.Vypočítajte obvod a obsah trojuholníka ABC, ak pre jeho vrcholy platí:
A[0;1;2], B[1;2;0], C[2;0;1]
Riešenie:
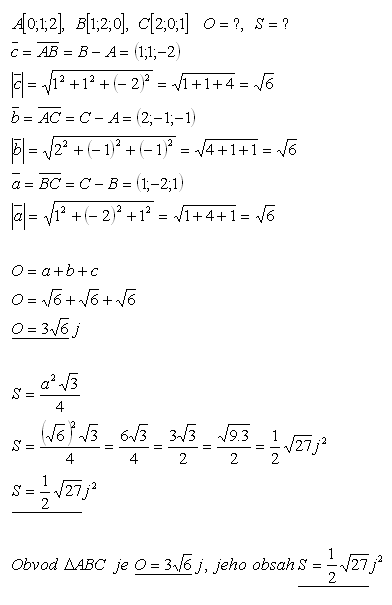
19.V trojuholníku ABC sú dané vrcholy A, B a ťažisko T. Určite súradnice vrcholu C ak platí
A[3;3;3], B[-2;1;2], T[0;-1;0], C[x,y,z]
Riešenie:
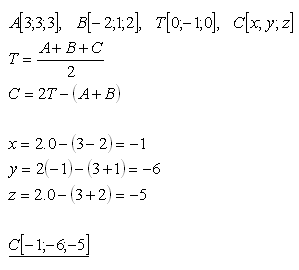
Tretí vrchol ΔABC je C[-1;-6;-5].
20.Vektor u zapíšte ako lineárnu kombináciu vektorov v a w ak platí:
Riešenie: