Zlomyseľné čísla

Existuje otázka, či je možné vytvárať prvočísla podľa všeobecne platného vzorca. Švajčiarsky matematik L. Euler (1707 – 1783) navrhol vzorec p = n² + n + 41.

n = 1,   p = 43 – prvočíslo

n = 2,   p = 47 – prvočíslo

n = 3,   p = 53 – prvočíslo

n = 40, p = 1681 – nie je prvočíslo, lebo 1681 = 41.41

Francúzsky matematik P. Fermat (1601 – 1665) skúmal vzorec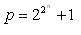

n = 1,   p = 2^₂1 + 1 = 5 – prvočíslo

n = 2,   p = 2^₂2 + 1 = 17 – prvočíslo

n = 3,   p = 2^₂3 + 1 = 257 – prvočíslo

n = 36, p = 2^₂36 + 1  nie je prvočíslo, lebo je deliteľné číslom 2 748 779 069 441

 

Iný postup pri hľadaní prvočísiel navrhol francúzsky matematik M. Mersenne (1588 – 1648). Navrhol vzorec pre výpočet „Mersenierových prvočísiel“:

p = 2ⁿ – 1. Aby 2ⁿ – 1 bolo prvočíslo, musí byť aj n prvočíslo.

n = 2, p = 2²- 1 = 5 – prvočíslo

n = 3, p = 2³ – 1 = 7 – prvočíslo

n = 5, p = 2⁵ – 1 = 31 – prvočíslo

n = 11, p = 2¹¹ – 1 = 2047 – nie je prvočíslo, lebo 2047 = 23.89

Vždy najmenej jedno „zlomyselné číslo“ nádejné úvahy pokazilo. Doteraz je známych 24 „Mersenierových prvočísiel“ pre exponenty

n = 2,3,5,7,13,17,19,31,61,89,107,127,521,607,1279,2203,2281,3217,4253, 4423,9689,9941,11213,19937.

Pravdepodobne doteraz najväčším „Mersenierovým prvočíslom“ je prvočíslo p = 2¹⁹⁹³⁷ – 1 , vypočítané počítačom. Má vyše 6000 číslic. Prvočíselné „dvojičky“ sú dve prvočísla, medzi ktorými stojí jedno zložené číslo

 

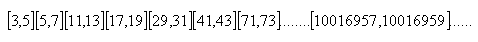
„Trojičky“ sú jediné 3,5,7. „Štvoričky“ neexistujú.

 Literatúra: Opava,Z.: Matematika kolem nás, Praha, Albatros 1989.

---