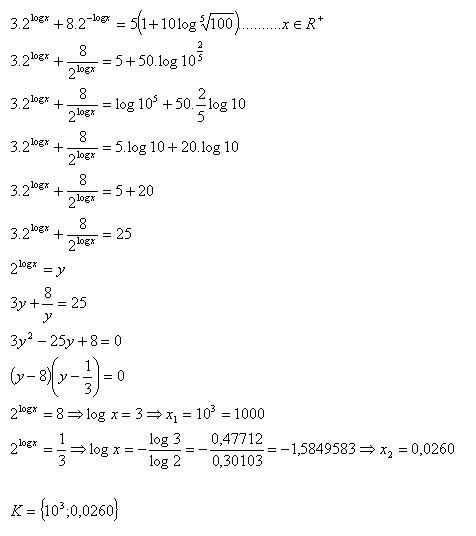Priklady.euMatematikaLogaritmické rovniceLogaritmické exponenciálne rovnice

Logaritmické exponenciálne rovnice

1. Riešte rovnicu:

log₃(2^x - 7) = 2 2^x > 7

Riešenie:
log₃(2^x - 7) = 2
log₃(2^x - 7) = log₃3²
2^x – 7 = 3²
2^x – 7 = 9
2^x = 16
2^x = 2⁴
x = 4

K = {4}

2. Riešte rovnicu:

log₂( 9- 2^x) = 3 – x 2^x < 9

Riešenie:

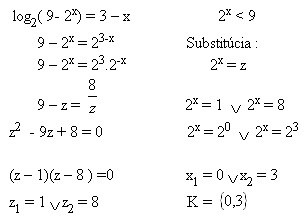
logexporov

3. Riešte rovnicu:

log₃( 1 + log₃(2^x-7)) = 1 2^x > 7

Riešenie:
log₃( 1 + log₃(2^x-7)) = 1
log₃( 1+ log₃(2^x-7)) = log₃3
1 + log₃(2^x-7) = 3
log₃(2^x-7) = 2
log₃(2^x-7) = log₃9
2^x-7 = 9
2^x = 16
2^x = 24
x = 4

K = {4}

4. Riešte rovnicu:

log₃(3^x- 8) = 2 – x 3^x > 8

Riešenie:

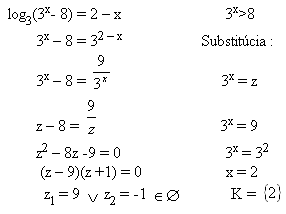
logexporov2

5. Riešte rovnicu:

logexporov3zad

Riešenie:

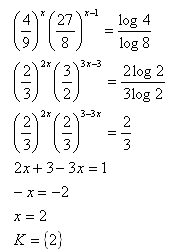
logexporov3

6.V množine R riešte:

Riešenie:

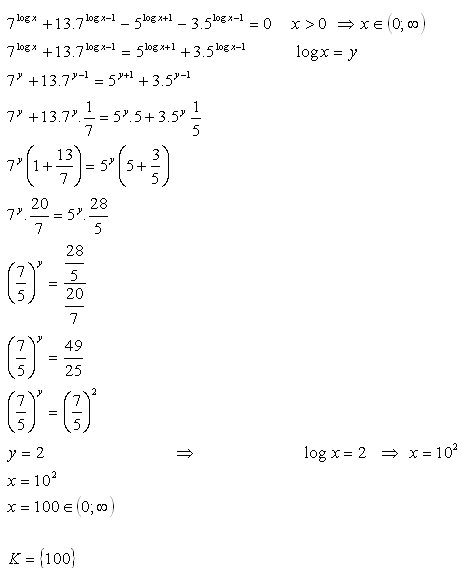
7. V množine R riešte:

Riešenie:

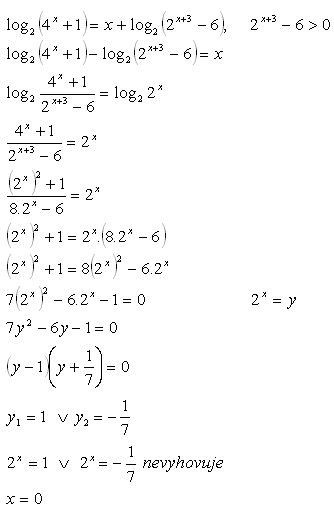
8. V množine R riešte:

Riešenie:

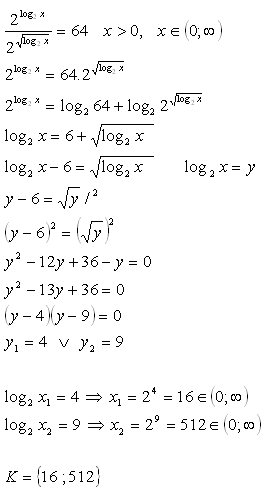
9. V množine R riešte:

Riešenie:

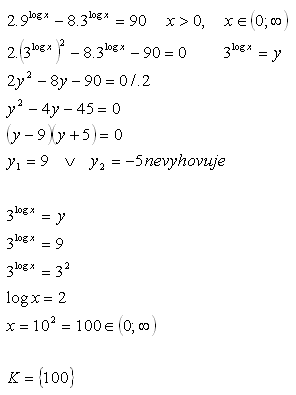
10.V množine R riešte:

Riešenie:

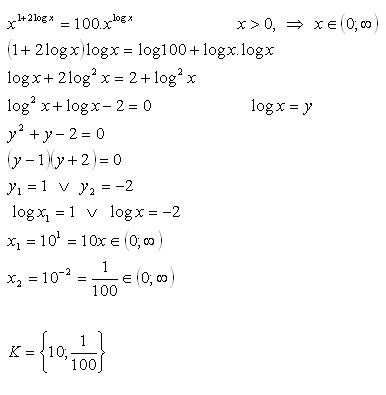
11.V množine R riešte:

logaritmicke-exponencialne-rovnice-11-1

Riešenie:

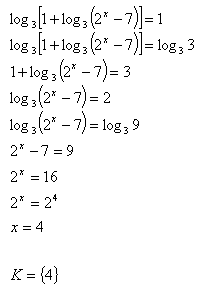
logaritmicke-exponencialne-rovnice-11-2

12.V množine R riešte:

logaritmicke-exponencialne-rovnice-12-1

Riešenie:

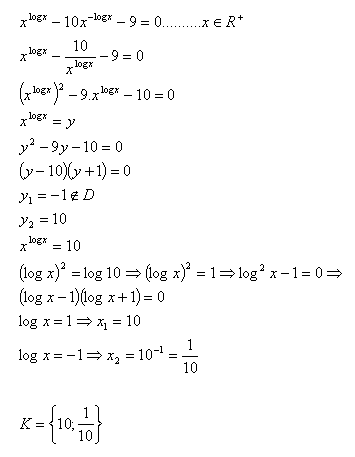
logaritmicke-exponencialne-rovnice-12-2

13.V množine R riešte:

logaritmicke-exponencialne-rovnice-13-1

Riešenie:

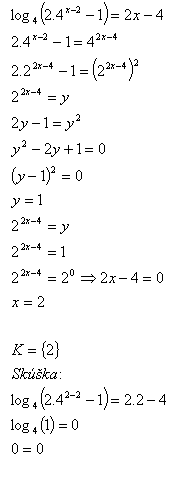
logaritmicke-exponencialne-rovnice-13-2

14.V množine R riešte:

logaritmicke-exponencialne-rovnice-14-1

Riešenie:

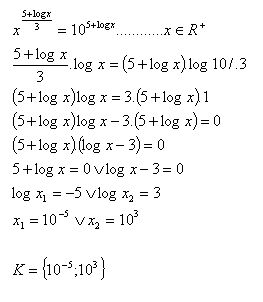
logaritmicke-exponencialne-rovnice-14-2

15.V množine R riešte:

logaritmicke-exponencialne-rovnice-15-1

Riešenie:

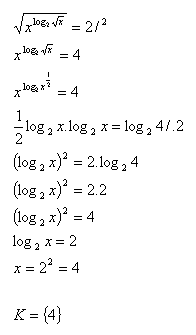
logaritmicke-exponencialne-rovnice-15-2

16.V množine R riešte:

logaritmicke-exponencialne-rovnice-16-1

Riešenie:
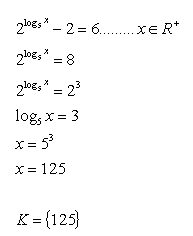
logaritmicke-exponencialne-rovnice-16-2

17.V množine R riešte:

logaritmicke-exponencialne-rovnice-17-1

Riešenie:

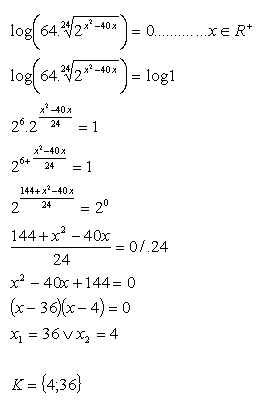
logaritmicke-exponencialne-rovnice-17-2

18.V množine R riešte:

logaritmicke-exponencialne-rovnice-18-1

Riešenie:

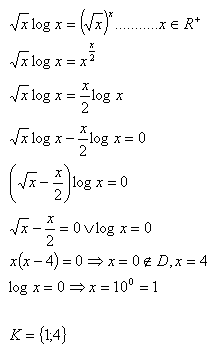
logaritmicke-exponencialne-rovnice-18-2

19.V množine R riešte:

logaritmicke-exponencialne-rovnice-19-1

Riešenie:

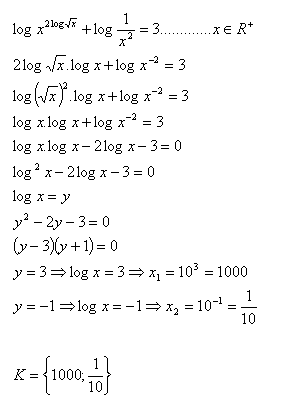
logaritmicke-exponencialne-rovnice-19-2

20.V množine R riešte:

logaritmicke-exponencialne-rovnice-20-1

Riešenie:

logaritmicke-exponencialne-rovnice-20-2