Variácie
1. Definujte a charakterizujte variácie a variácie s opakovaním.
Riešenie:
Variácie
Variácia k-tej triedy z n prvkov je každá usporiadaná k-tica rôznych prvkov, vybraných z n-prvkovej množiny. V k-tici záleží na poradí prvkov. V k-tici sa ani jeden z prvkov neopakuje.
Počet variácií:
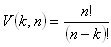 Variácie s opakovaním
Variácie s opakovaním
Variácia k-tej triedy z n prvkov s opakovaním je každá usporiadaná k-tica prvkov vybraných z n-prvkovej množiny. V k-tici sa môžu prvky ľubovoľne opakovať.
Počet variácií s opakovaním:
V*(k,n) = n
k
2. Daná je množina M = {a,b,c,d}. Z prvkov tejto množiny vytvorte variácie 2.triedy bez opakovania a s opakovaním. Vypočítajte ich počet.
Riešenie:
a) Variácie:
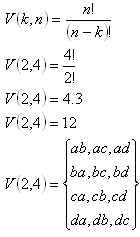
b) Variácie s opakovaním:
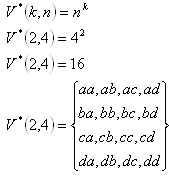
3. Do školského výboru zvolili 7 žiakov. Koľkými spôsobmi sa dá z nich vybrať predseda, podpredseda, tajomník a pokladník?
Riešenie:
Sú to variácie: n = 7, k = 4
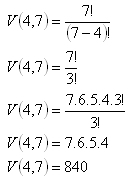
Funkcionári výboru sa dajú vybrať 840 spôsobmi.
4. Osem študentov si sľúbilo, že si z prázdninových ciest navzájom pošlú pohľadnice.
Koľko pohľadníc rozoslali?
Riešenie:
Sú to variácie: n = 8, k = 2
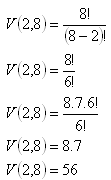
Študenti rozoslali 56 pohľadníc.
5. Z koľkých rôznych prvkov môžeme vytvoriť 240 variácií 2.triedy?
Riešenie:
Sú to variácie: n = x, k = 2
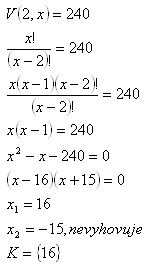
Potrebujeme 16 prvkov.
6. Ak sa počet prvkov zväčší o 2, zväčší sa počet variácií 3. triedy o 384. Koľko je prvkov?
Riešenie:
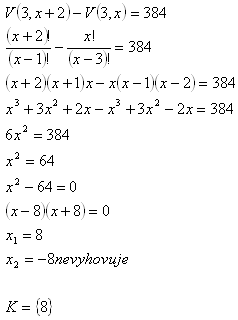
Prvkov je 8.
7. Vo vrecku je 6 rôznych lístkov označených číslicami 1 až 6. Koľkými rôznymi spôsobmi môžeme postupne, s prihliadnutím na poradie vybrať tri z nich, ak vybrané lístky sa do vrecka
a) nevracajú.
b) vracajú.
Riešenie:
a) nevracajú
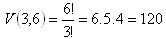
b) vracajú
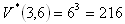
Kartičky môžeme z vrecka vybrať 120 alebo 216 spôsobmi.
8. Počet variácií bez opakovania 3.triedy z x prvkov je o 225 menší než počet variácií 3.triedy s opakovaním z tých istých prvkov. Koľko je prvkov?
Riešenie:
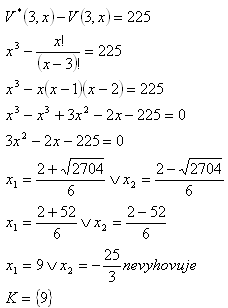
9. Počet trojčlenných variácií bez opakovania je 10 násobkom dvojčlenných variácií bez opakovania tej istej množiny prvkov. Koľko prvkov má táto množina?
Riešenie:
Počet prvkov množiny: x
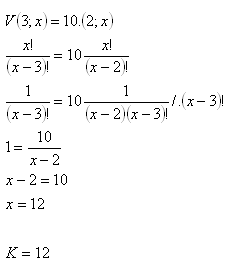
Počet prvkov množiny je x = 12
10.Hoďme troma kockami – bielou, modrou, žltou.
- a.) Koľko rôznych výsledkov môžeme dostať?
- b.) Koľko rôznych súčtov môže padnúť?
- c.) Koľkými spôsobmi môže padnúť súčet 13
Riešenie:
- a.) V/(k;n) = nk , V/(3;6) = 63 = 216
- b.) Môže padnúť súčet : 3;4;5;6;7;8;9;10;11;12;13;14;15;16;17;18, n = 16súčtov
- c.) Súčet 13:
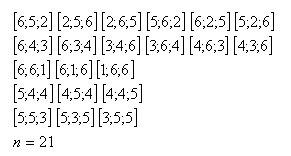
- a.) Môžeme dostať 216 rôznych výsledkov.
- b.) Môže padnúť 16 rôznych súčtov bodov
- c.) Súčet 13 môže padnúť 21 spôsobmi