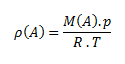Výpočty pre čisté látky
Úvodom tejto kapitoly sa zameriame na základné vzťahy potrebné pri chemických výpočtoch. Zadefinujeme si ich jednotky, značenie a výpočet. Predpokladám základné znalosti jednotiek, chemických a fyzikálnych pojmov.
V chemickej praxi pracujeme s rôznymi množstvami látok. Množstvo látky vyjadrujeme prostredníctvom počtu častíc, hmotnosti látky, alebo jej objemu.
Látkové množstvo n určuje množstvo chemicky rovnorodej látky podľa počtu jej základných častíc (entít). Jednotkou látkového množstva je mol (mol). Mol je látkové množstvo sústavy obsahujúcej práve toľko elementárnych jedincov (entít), koľko je atómov v 0,012 kg (presne) nuklidu uhlíka 12C. Konštanta udávajúca počet časíc v jednom mole je Avogadrova konštanta NA = 6,022 . 1023 mol-1.
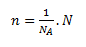
kde NA je počet častíc v jednom mole látky a N je ľubovoľný počet častíc.
Relatívna atómová hmotosť Ar prvku vyjadruje pomer priemernej hmotnosti atómu prvku k atómovej hmotnostnej konštante mu= 1,66056 . 10-27 kg. Atómová hmotnostná konštanta sa rovná 1/12 hmotnosti neutrálneho atómu uhlíka.
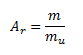
Mólová hmotnosť je hmotnosť jedného molu chemicky čistej látky, v SI má jednotku kg.mol-1, v praxi sa však najčastejšie používa g.mol-1.
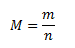
kde m je hmotnosť látky v gramoch, n je látkové množstvo látky v moloch.
Mólový objem látky Vm sa definuje ako podiel jej objemu V a látkového množstva n.
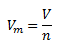
Mólový objem látky pri normálnych podmienkach (273,15 K a 101325 Pa) sa nazýva normálny mólový objem Vmn. V prípade ideálneho plynu je hodnota normálneho mólového objemu Vmn= 22,41 dm3.mol-1. (Je to Avogadrov zákon, podľa ktorého majú rovnaké objemy rozličných plynov pri rovnakom tlaku a teplote rovnaký počet molekúl)
Stavová rovnica ideálneho plynu je vysvetlená vo fyzikálnej časti stránky.
p.V=n.R.T
Pre ideálny plyn zároveň platia tieto zákony:
Boyelov-Mariottov zákon, podľa ktorého je pre dané množstvo plynu súčin jeho tlaku a objemu pri konštantnej teplote konštantný
p.V=const, resp. p0V0=p1V1
Gay-Lussacov zákon, ktorý vyjadruje lineárny rast objemu plynu v závislosti od teploty pri konštantnom tlaku
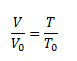
Charlesov zákon, ktorý vyjadruje lineárny rast tlaku plynu v závislosti od teploty pri konštantnom objeme
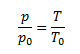
Daltonov zákon-celkový tlak plynnej zmesi p sa rovná súčtu parciálnych tlakov všetkých jej zložiek
p=∑pi pri konštantnej teplote
Parciálny tlak i-tej zložky pi je tlak, ktorý by zložka mala, keby sama zaberala pri danej teplote celý objem sústavy. Pre parciálny tlak zložky platí
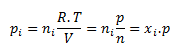
kde ni je látkové množstvo i-tej zložky, n je látkové množstvo zmesi a xi je molový zlomok i-tej zložky
Hustota látky je podiel hmotnosti látky a jej objemu. Jednotkou hustoty v sústave SI je kilogram na meter kubický, kg.m-3, prípadne gram na centimeter kubický g.cm-3.
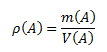
Vzťah pre hustotu plynu možno odvodiť zo stavovej rovnice: