Kombinácie

1. Charakterizujte kombinácie a kombinácie s opakovaním.

Riešenie:

a) Kombinácie k-tej triedy z n prvkov (bez opakovania)
Kombinácie k-tej triedy z n prvkov (bez opakovania) je každá k-tica rôznych prvkov vybraných z n prvkovej množiny (v k-tici nezáleží na poradí prvkov).


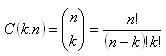
b) Kombinácie k-tej triedy z n prvkov (s opakovaním)
Kombinácie k-tej triedy z n prvkov (s opakovaním) je každá k-tica prvkov vybraných z n-prvkovej množiny (v k-tici nezáleží na poradí prvkov a môžu sa v nej prvky ľubovoľne opakovať).

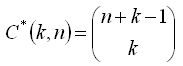
2. V rovine je 6 rôznych bodov (žiadne 3 neležia na jednej priamke). Koľko rôznych úsečiek dostaneme pospájaním všetkých týchto bodov navzájom?

Riešenie:


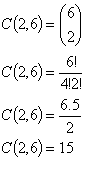
Dostaneme 15 rôznych úsečiek.

3. Na kružnici je rozmiestnených 9 bodov. Koľko existuje rôznych trojuholníkov, ktorých vrcholy sú tieto body?

Riešenie:


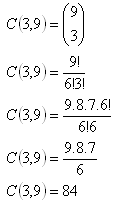
Existuje 84 takýchto trojuholníkov.

4.a) Odvoďte vzorec pre počet N uhlopriečok vypuklého n-uholníka!
b) Koľko uhlopriečok má vypuklý 10-uholník?

Riešenie:



Vypuklý 10-uholník má 35 uhlopriečok.

5. Koľkorakým spôsobom je možné rozdať 32 hracích kariet 4 hráčom?

6. Skúšajúci má pripravených 20 príkladov z aritmetiky a 30 z geometrie. Na písomku chce dať:

Riešenie:


Skúšajúci má v prvom prípade 495 900 možností, v druhom 8700 možností.

7. Na pomaturitnom stretnutí po rokoch si účastníci štrngli pohármi. Uskutočnilo sa 253 štrngnutí. Koľko účastníkov bolo na stretnutí?

Riešenie:

Na stretnutí bolo 23 účastníkov.

8. Ak sa zväčší počet prvkov o 8, zväčší sa počet kombinácií 2. triedy bez opakovania 11 krát. Pre koľko prvkov to platí?

Riešenie:

Platí to pre 4 prvky.

9. Pre ktoré x є N platí :

Riešenie:


Nerovnica platí pre čísla 1, 2, 3, 4, 5 a 6.

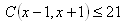
10. Dve skupiny majú spolu 26 prvkov a 160 kombinácií 2. triedy bez opakovania.
Koľko prvkov je v každej skupine?

Riešenie:

x – počet prvkov v prvej skupine
y – počet prvkov v druhej skupine

11. V cukrárni majú 5 druhov zmrzlín. Otec chce pre rodinu kúpiť 15 porcií.
Koľkými spôsobmi môže zmrzlinu kúpiť?

Riešenie:
 

Otec môže zmrzlinu kúpiť 3876 spôsobmi.

12. Koľko potrebujeme prvkov, aby sme z nich mohli vytvoriť 15 kombinácií 2.triedy s opakovaním?

Riešenie:

K = {5}

Potrebujeme 5 a viac prvkov.