Kombinace
1. Charakterizujte kombinace a kombinace s opakováním.
Řešení:
a)
Kombinace k-té třídy zn prvků (bez opakování)
Kombinace k-té třídy z n prvků (bez opakování) je každá k-tice různých prvků vybraných z n. prvkové množiny (v k-tici nezáleží na pořadí prvků).
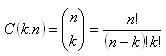
b)
Kombinace k-té třídy zn prvků (s opakováním)
Kombinace k-té třídy z n prvků (s opakováním) je každá k-tice prvků vybraných z n-prvkové množiny (v k-tici nezáleží na pořadí prvků a mohou se v ní prvky libovolně opakovat).
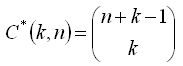
2. V rovině je 6 různých bodů (žádné 3 neleží na jedné přímce). Kolik různých úseček dostaneme pospojováním všech těchto bodů navzájem?
Řešení:
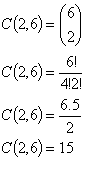
Dostaneme 15 různých úseček.
3. Na kružnici je rozmístěno 9 bodů. Kolik existuje různých trojúhelníků, jejichž vrcholy jsou tyto body?
Řešení:
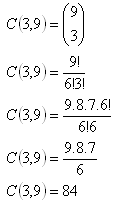
Existuje 84 takových trojúhelníků.
4.a) Odvoďte vzorec pro počet N úhlopříček vypouklého mnohoúhelníka!
b) Kolik úhlopříček má vypouklý 10-úhelník?
Řešení:
Vypouklý 10-úhelník má 35 úhlopříček.
5. Kolik způsoby je možné rozdat 32 hracích karet 4 hráčům?
Řešení:
Karty můžeme rozdat 6545 způsoby.
6. Zkoušející má připravených 20 příkladů z aritmetiky a 30 z geometrie. Na písemku chce dát:
a) 3 aritmetické a 2 geometrické příklady
b) 1 aritmetický a 2 geometrické příklady
Kolik má možností sestavení různých zadání?
Řešení:
Zkoušející má v prvním případě 495 900 možností, ve druhém 8700 možností.
7.Na pomaturitním setkání po letech si účastníci cinkli sklenicemi. Uskutečnilo se 253 cinknutí. Kolik účastníků bylo na setkání?
Řešení:
Na setkání bylo 23 účastníků.
8. Pokud se zvětší počet prvků o 8, zvětší se počet kombinací 2. třídy bez opakování 11 krát. Pro kolik prvků to platí?
Řešení:
Platí to pro 4 prvky.
9. Pro které x є N platí :
Řešení:
Nerovnice platí pro čísla 1, 2, 3, 4, 5 a 6.
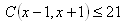
10. Dvě skupiny mají celkem 26 prvků a 160 kombinací 2. třídy bez opakování. Kolik prvků je v každé skupině?
Řešení:
- x - počet prvků v první skupině
- y - počet prvků v druhé skupině
11. V cukrárně mají 5 druhů zmrzlin. Otec chce pro rodinu koupit 15 porcí. Kolika způsoby může zmrzlinu koupit?
Řešení:
Otec může zmrzlinu koupit 3876 způsoby.
12. Kolik potřebujeme prvků, abychom z nich mohli vytvořit 15 kombinací 2.třídy s opakováním?
Řešení:
K = {5}
Potřebujeme 5 a více prvků.