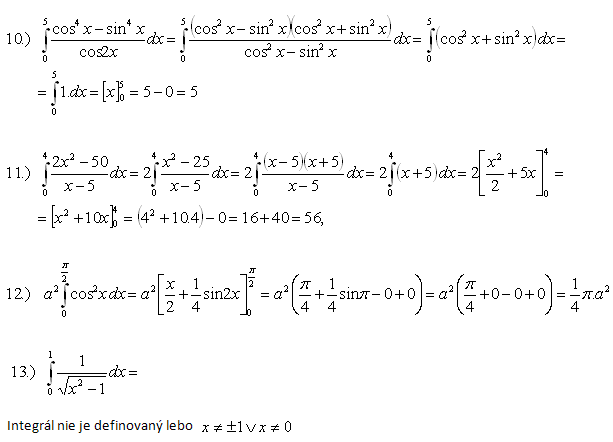Určitý integrál - Leibnitz a Newtonova metoda
1. Jaké vlastnosti má určitý integrál?
Řešení:
Leibniz – Newtonova formula:
Nechť funkce f (x) je spojitá v intervalu <a,b>, (kde a je dolní ab horní hranice intervalu). Pak platí Leibniz - Newtonova formule:
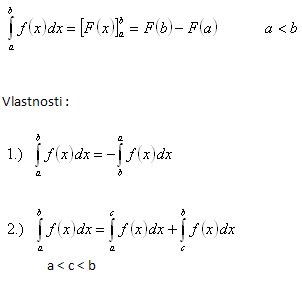
2.Vypočtěte integrály:
Řešení:
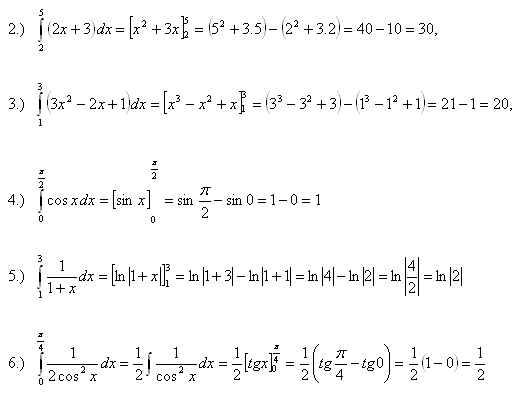
3. Vypočtěte integrály:
Řešení:
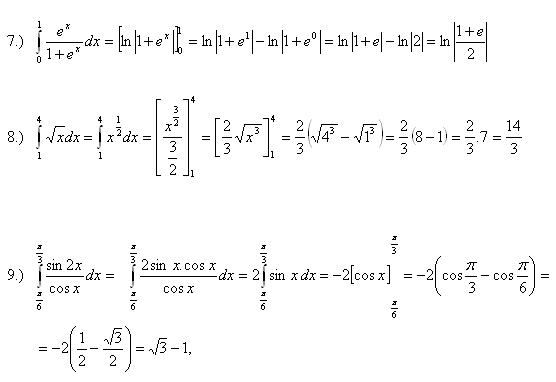
4.Vypočtěte integrály:
Řešení: