Deformace pevných látek
1.Co je třeba vědět o deformaci pevných látek?
Řešení:
Deformace je změna tvaru tělesa působením vnějších sil.
Deformácia:
- a.) elastická – pružná, dočasná
- b.) plastická – nepružná, trvalá
Deformace může být způsobena tahem, tlakem, ohybem, smykem, krutem nebo kombinovaná
Deformace tahem:
Absolutní prodloužení:
Δl = l – l0
Relativní prodloužení:
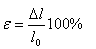
Normálové napětí:
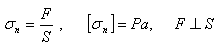
Hookeův zákon:
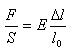
Hookeův zákon platí pouze po mez pružnosti
Křivka deformace:
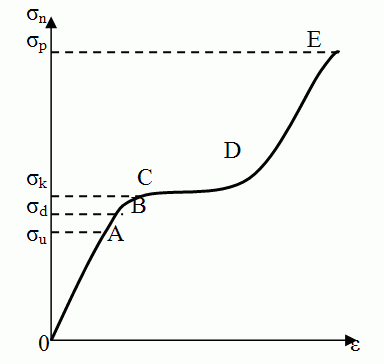
σu = mez úměrnosti
σd = σE = mez pružnosti (dovolené napětí)
σk = mez klzu
σp= mez pevnosti
E = Youngův modul pružnosti v tahu
2.Zjistěte, zda se přetrhne železný drát o průměru 2 mm, pokud je napínán silou 1 kN.(σE = 314 MPa)
Řešení:
Rozbor:
d = 2 mm, r = 1 mm = 10-3m, F = 103N, σE = 314MPa
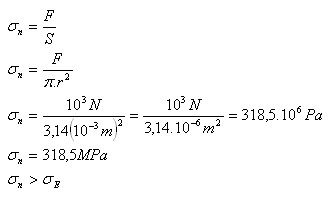
Protože σn > σE, železný drát se přetrhne.
3.Vypočítejte relativní prodloužení lana původní délky 10 m, pokud se při deformaci prodlouží o 40 mm.
Řešení:
Rozbor:
l0 = 10 m, Δl = 40 mm = 0,04 m
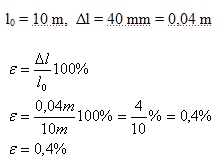
Relativní prodloužení lana je ε = 0,4%.
4.Jak se změní normálové napětí drátu, pokud se tahová síla působící na drát zvětší 4 krát a průměr drátu 2 krát?
Řešení:
Rozbor:
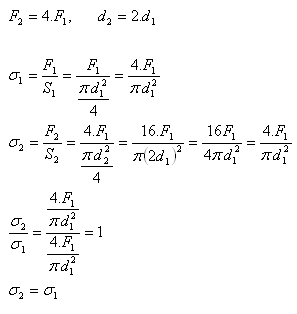
Normálové napětí se v drátě nezmění.
5.Jaký musí být poloměr měděného drátu (σp = 2.108 Pa), aby se účinkem síly 500 N neprotrhl?
Řešení:
Rozbor:
F=500N, σp = 2.108 Pa
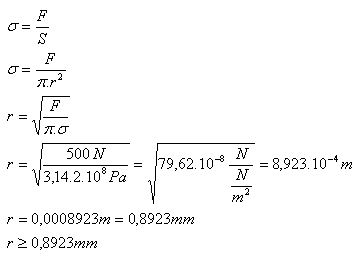
Pro poloměr drátu musí platit r> = 0,89 mm
6.Jakou největší délku musí mít železný drát zavěšený ve vertikální poloze, aby se práci navíc působením vlastní tíhy?
Řešení:
Rozbor:
g = 9,81 m.s-2, ρ (Fe) = 7800 kg.m-3= 7,8.103 kg.m-3, σp = 314.106Pa
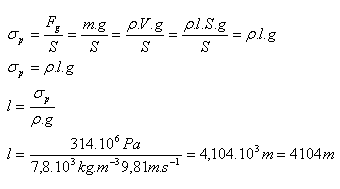
Délka drátu může být maximálně 4104 m.
7.Jak velkou silou je napjatá struna kytary dlouhá 0,65 ma průřezu 0,325 mm2, jestliže se při napínání prodloužila o 5 mm. (E = 220 GPa)
Řešení:
Rozbor:
l0 = 0,65 m, Δl = 5.10-3m, S = 0,325.10-6m2, E = 220.109Pa
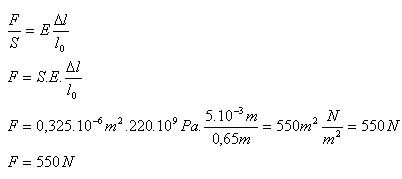
Struna kytary je napjatá silou F = 550 N.
8. Hliníkový drát s původní délkou 4,2 ma průměru 1,1 mm se působením síly 0,23 kN prodloužil o 15,2 mm. Určitě modul pružnosti v tahu E!
Řešení:
Rozbor:
l0 = 4,2 m, r = 0,55.10-3m, F = 0,23.103N, Δl = 15,2.10-3m
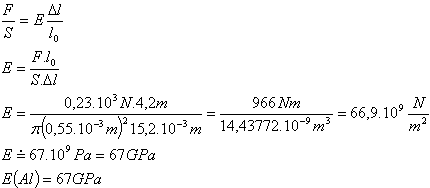
Modul pružnosti v tahu hliníku je E (Al) = 67 GPa.
9.Na konec ocelové tyče (E = 220 GPa) s délkou 1,5 m umístěné ve vertikální poloze má být zavěšeny závaží o hmotnosti 500 kg. Jaký průměr tyče zvolíme, pokud chceme, aby se tyč po zavěšení závaží neprodloužila o více než 0,3 mm. (Vlastní tíhu tyče neuvažovat)
Řešení:
Rozbor:
l0 = 1,5 m, m = 500 kg, Δl = 3.10-4m, E = 220 GPa = 220.109Pa, g = 10 m.s-2
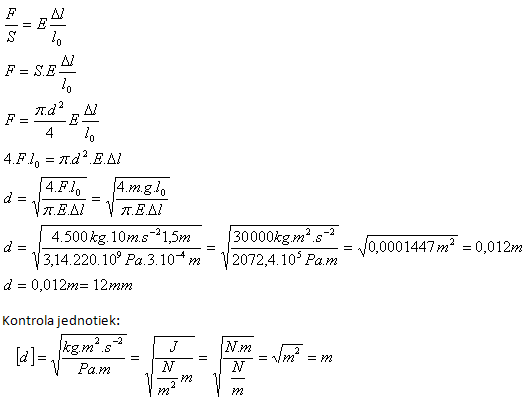
Průměr tyče zvolíme d = 12 mm.
10.Určete práci, kterou je třeba provést, aby se ocelová tyč (E = 220 GPa) délky 1m, průřezu 1 cm2 prodloužila při pružné deformaci v tahu o 1 mm.
Řešení:
Rozbor:
l0 = 1m, Δl = 1mm = 1.10-3m, S = 1cm2 = 1.10-4m2, E = 220.109Pa
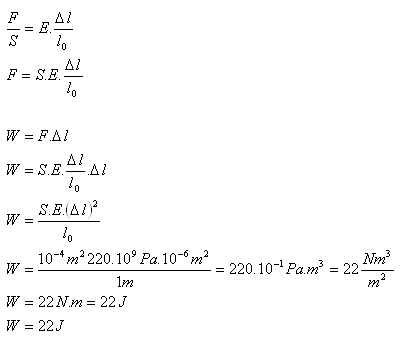
Aby se ocelová tyč prodloužila třeba vykonat práci W = 22 J.
11.Ocelová zkušební tyčinka o průměru 15mm se protrhla silou 1,63 .105 N. Určete mez pevnosti oceli.
Řešení:

12.Osobní výtah o hmotnosti 500 kg drží 3 ocelová lana, každé o průměru 1 cm. Vypočítejte napětí v každém ocelovém laně. (Vlastní tíhu lana zanedbejte).
Řešení:
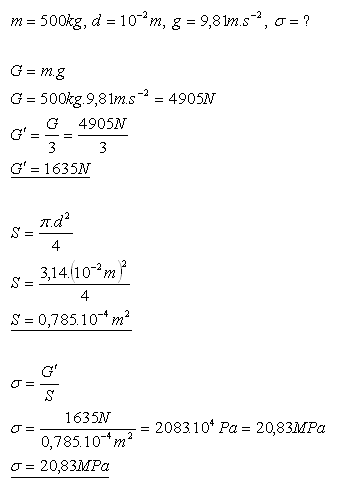
Napětí v ocelovém laně je 20,83 MPa.
13.Jaký musí být poloměr měděného drátu, aby se působením síly 500 N práci navíc.
Řešení:
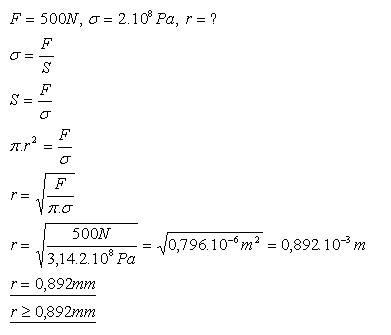
Poloměr měděného drátu musí být rovný nebo větší než 0,892 mm
14. Ocelový drát s délkou 3m a průřezem 1,2 mm2 se působením deformujících sil prodlouží o 8mm. Vypočítejte velikost deformujících sil.
Řešení:
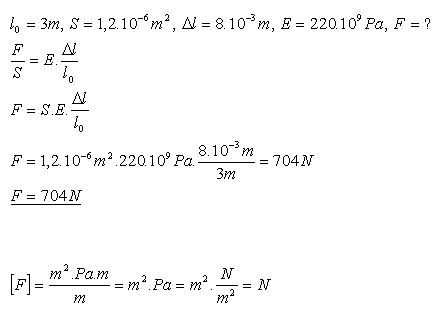
Deformujíci síla je 704 N.
15.Při výrobě dílců z předpjatého železobetonu se napínaly ocelové pruty dlouhé 6 metrů silou 60000 N. Vypočítejte prodloužení ocelových tyčí, pokud mají průměr 10 mm.
Řešení:
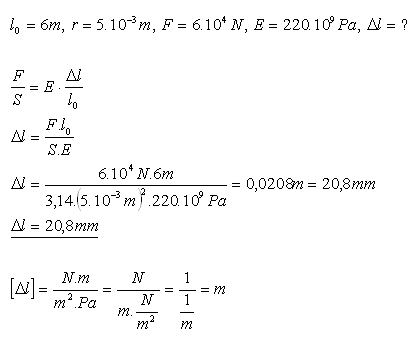
Ocelové tyče se prodlouží o 20,8 mm.
16.Mosazný drát délky 1,1 m s průřezu 4.10-6m2 se deformoval tahem silou 80N, čímž se prodloužil o 0,2 mm. Vypočítejte modul pružnosti mosazi.
Řešení:
Rozbor:
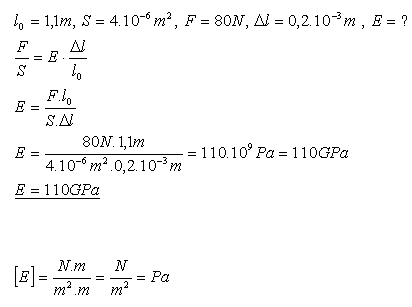
Modul pružnosti mosazi je 110 GPa.
17.Ocelová tyč je na jednom konci upevněna. Jak se změní její teplota, pokud na volném konci vyvoláme silovým působením tlak 5 MPa?
Řešení:
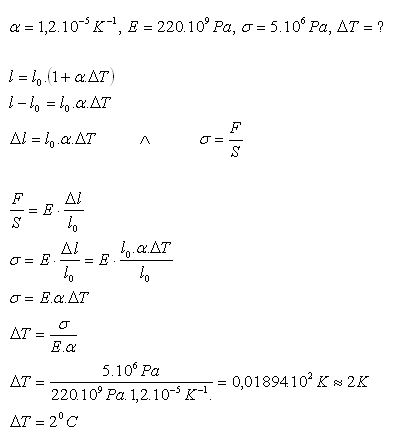
Ocelové tyč se ohřeje o přibližně 20C.
18.Víko s průměrem 32cm třeba připevnit k otvoru tlakové nádoby 24 šrouby. Tlak plynu v nádobě je 6MJ. Jaký plošný obsah průřezu šroubů třeba zvolit?
Řešení:
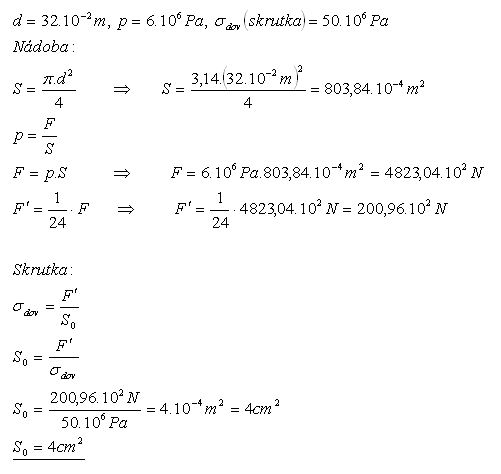
Plošný obsah průřezu šroubu je 4cm2.
19.Dvousloupový hydraulický lis stlačuje materiál silou 600 kN. Sloupy lisu jsou ocelové a mají průměr 80 mm. Jaké je normálové napětí ve sloupu?
Řešení:
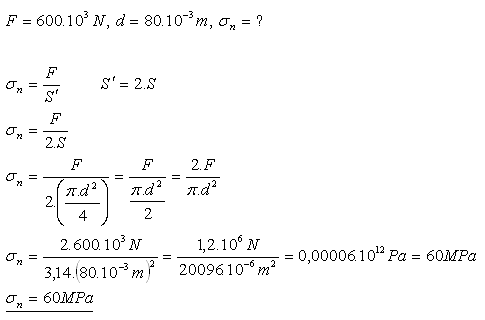
Normálové napětí je 60 MPa.
20.Na ocelovém laně příčného průřezu 2 cm2 je zavěšeno břemeno o hmotnosti 4000 kg. Jaké je relativní prodloužení lana?
Řešení:
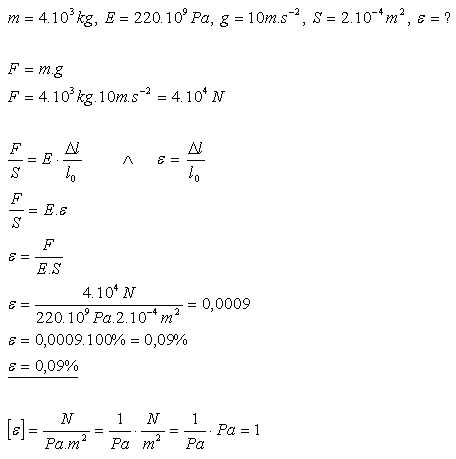
Relativní prodloužení lana je 0,09%.