Ludolfovo číslo v Číne
Staročínska matematika.
Babylonská a Egyptská matematika sa rozvíjala na pobreží veľkých riek Eufratu, Tigrisu a Nílu. Aj na pobreží veľrieky Jang – c/ - tiang žili národy vysokej civilizácie s bohatými matematickými znalosťami – Číňania. Okolo roku 200 pred n. l. Čang Cchang vytvoril ústredné dielo čínskej matematiky „Matematika v deviatich knihách“, ktorá bola dopĺňaná, komentovaná a opisovaná čínskymi matematikmi niekoľko storočí. V ich dielach bolo π = 3.
Čang Cheng (78 – 139 n. l.) prišiel k záveru, že „pomer druhej mocniny dĺžky kružnice a druhej mocniny obvodu štvorca tejto kružnici opísaného je 5:8“.
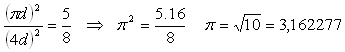
Jeden z najväčších staročínskych matematikov, komentátor a redaktor „Matematiky o deviatich knihách“ Liou Chueje (5. stor. n.l.) prospel k približnej hodnote čísla π . V jeho metóde sa obsah kruhu nahrádza obsahom vpísaného a opísaného n – uholníka. Zdôrazňuje: „Čím jemnejšie budeme deliť strany n – uholníkov, tým viac sa ich obvody budú približovať k dĺžke kružnice“. Pri svojom výpočte použil 3072-uholníky a určil π = 3,14159.
Iný významný čínsky matematik Cu – Čchung – č (430 – 501) je autorom vyjadrenia čísla π pomocou zlomku : π = 355/113 = 3,141592, ktoré v desiatkovej sústave zapísal takto: π = 3čang 1čchi 4achun 1fen 5li 9chav 2miao Slovné vyznačenia jednotlivých rádov sa neskôr vynechali a zapisovali sa len číslice. Desatinnú čiarku nahradil znak „tien“. Celé dejiny matematiky v Číne svedčia o vynikajúcej úrovni jej tvorcov. Čerpali z nej matematici Japonska, Indie, islamských zemí aj Európy.