Astrofyzika
1.Jak se v astrofyzice určují vzdálenosti, hmotnost a jasnost hvězd?
Řešení:

2.Jak se získávají informace o hvězdách a vesmíru?
Charakterizujte:
- Wienův posuvný zákon
- Stefan–Boltzmannův zákon
- Zářivý tok
- Zářivý výkon
- Charakteristiky Slunce
- Rozpínání vesmíru
Řešení:

3.Vypočítejte, za jaký čas proletí světlo ve vakuu vzdálenost rovnající se
- a) průměru sluneční soustavy (s = 80 AU)
- b) průměru galaxie (s = 30 kpc)
Řešení:
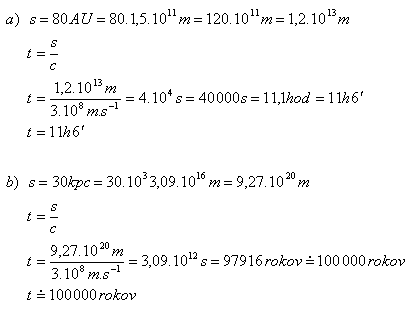
Světlo proletí průměr sluneční soustavy za 11 hodin, průměr galaxie za asi 100 000 let.
4.Vypočítejte střední hustotu látky ve Sluneční soustavě. Předpokládáme, že veškerou hmotnost soustavy vytváří Slunce (Mo = 2.1030kg) a že Sluneční soustava je koule s poloměrem R = 40 AU.
Řešení:
Rozbor:
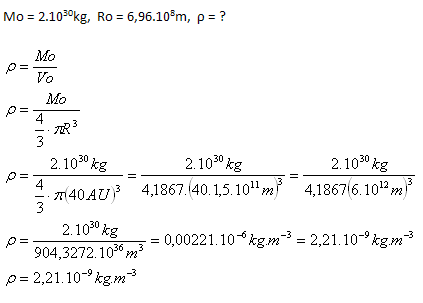
Hustota látky ve Sluneční soustavě je ρ = 2,21.10–9kg.m–3
5.Slunce obíhá kolem středu Galaxie rychlostí v = 250 km.s-1, přibližně po kružnici s poloměrem r = 10 kpc. Určete oběžnou dobu Slunce. Jak velkou gravitační silou je Slunce přitahováno ke středu Galaxie?
Řešení:
Rozbor:

- Oběžná doba Slunce kolem středu Galaxie je asi 250 milionů let.
- Slunce je ke středu Galaxie přitahováno gravitační silou Fg = 4.1020N.
6.Uvažujme o kulové hvězdokupě s hmotností MHK = 2.105Mo, která obíhá kolem středu Galaxie (MG = 1,4.1011Mo) po kružnici s poloměrem r = 12 kpc. Určete:
- a) sílu, kterou je hvězdokupa přitahována ke středu Galaxie
- b) dostředivé zrychlení hvězdokupy
- c) rychlost hvězdokupy vzhledem ke středu Galaxie
Řešení:
Rozbor:

- Síla, kterou je hvězdokupa přitahována ke středu Galaxie, je Fg = 5,4.1025N
- Dostředivé zrychlení hvězdokupy je a = 1,4.10–10m.s-2
- Rychlost hvězdokupy vzhledem ke středu Galaxie je v = 228 km.s-1
7.Odvoďte vzorec pro výpočet hmotnosti hvězdy (planety) pomocí její oběžnice.
Řešení:
Rozbor:
M = hmotnost hvězdy, m = hmotnost oběžnice, r = poloměr kruhové dráhy oběžnice, T = oběžná doba oběžnice, κ = 6,67.10–11N.m2.kg-2
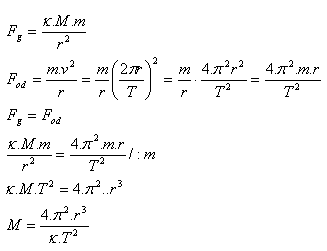
Hmotnost hvězdy se vypočte podle vztahu:
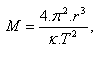
8.Vypočítejte hmotnost planety Mars pomocí měsíce Deimos, který obíhá kolem Marsu po kružnici s poloměrem r = 23,5.106m, s oběžným časem 1,26 dne (pozemského)
Řešení:
Rozbor:
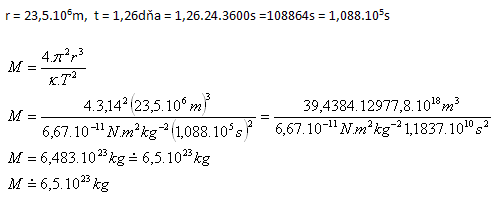
Hmotnost planety Mars je M = 6,5.1023kg.
9.Druhý Jupiterův měsíc Europa obíhá kolem Jupitera po kružnici s poloměrem r1 = 6,71.108m a s oběžnou dobou T = 3,88 dne. Vypočítejte, kolikrát je hmotnost Jupitera větší než hmotnost Země.
Řešení:
Jupiter + Europa : M1 + m1, r1 = 6,71.108m, T1 = 3,88 dne,
Země + Měsíc: M2 + m2, r2 = 3,844.108m = 1 měsíc = 30 dní
m1 – zanedbat, m2 – zanedbat vzhledem k M1 a M2
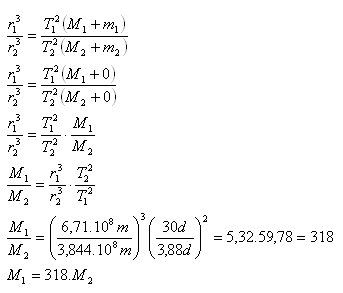
Hmotnost Jupitera je 318krát větší než hmotnost Země.
10.Součet hmotností složek dvojhvězdy je 3,5Mo, složky obíhají kolem společného těžiště s periodou T = 320 let. Určete vzájemnou polohu složek kolmou na směr zorného paprsku, kterou bychom viděli pod úhlem π = 3,1//, a vzdálenost dvojhvězdy od Slunce.
Řešení:
Rozbor:
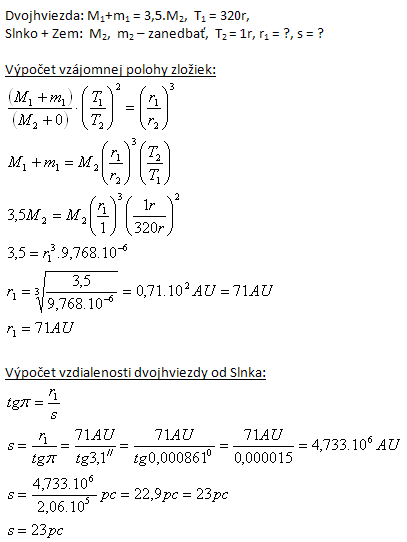
11.Zdánlivá hvězdná magnituda Slunce je -26,8m. Vypočítejte jeho absolutní magnitudu M.
Řešení:
Rozbor:
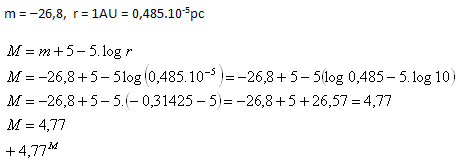
Absolutní hvězdná magnituda Slunce je + 4,77M
12.Do jaké vzdálenosti lze při měření vzdálenosti galaxií využít supernovu, která v nich zazářila, je-li její maximální absolutní magnituda –16M a máme dalekohled, kterým pozorujeme hvězdy do zdánlivé hvězdné magnitudy +22m?
Řešení:
Rozbor:
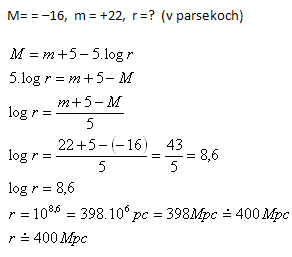
Dalekohled lze využít do vzdálenosti asi 400 Mpc.
13.Jakou paralaxu π má hvězda, pokud rozdíl zdánlivé a absolutní hvězdné magnitudy je +8
Řešení:
Rozbor:
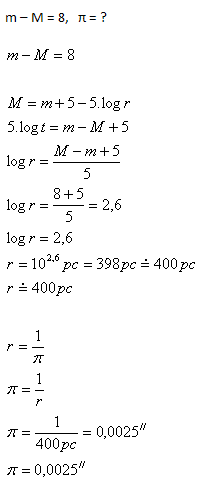
Hvězda má paralaxu π = 0,0025//.
14.Jaká je vlnová délka, na kterou připadá maximum vyzařování, a intenzita vyzařování hvězdy, která má teplotu 30 000K?
Řešení:
Rozbor:
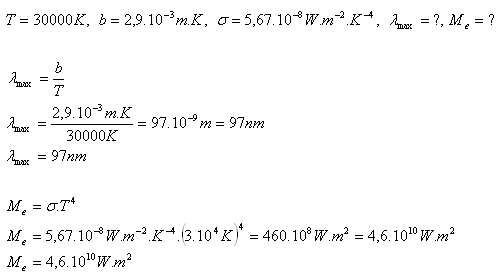
Vlnová délka je λ = 97nm, intenzita vyzařování hvězdy je Me = 4,6.1010W.m2.
15.Červený obr má povrchovou teplotu 3500K, poloměr R = 36.Ro, hmotnost M = 3,6 Mo. Vypočítejte jeho průměrnou hustotu ρ a zářivý výkon L. (σ = 5,67.10-8W.m-2.K–4)
Řešení:
Rozbor:

Průměrná hustota červeného obra je ρ = 0,11 kg.m-3 a jeho zářivý výkon L = 671.1028W.
16.Vypočítejte poloměr a průměrnou hustotu bílého trpaslíka, jehož hmotnost M = 2,35Mo, povrchová teplota T = 12 500K, zářivý výkon L = 0,0036 Lo. Ro = 6,96.108m, T0 = 5780K
Řešení:
Rozbor:

Poloměr bílého trpaslíka je R = 9.106m a jeho průměrná hustota ρ = 2,28.108kg.m–3.
17.Jaký zářivý tok dopadá ze Slunce na plochu o obsahu S = 1m2 (zářivý výkon Slunce je L = 3,83.1026W)
- na Venuši (r = 0,72AU)
- na Jupiter (r = 5,2AU)
Řešení:
Rozbor:
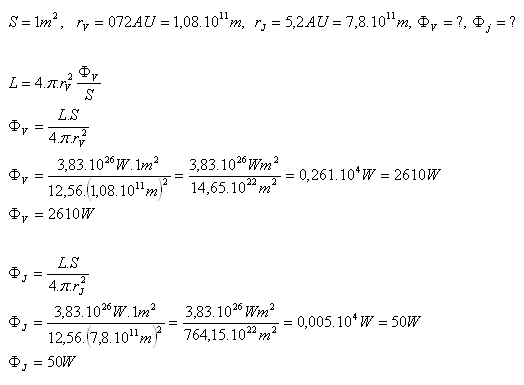
- Zářivý tok dopadající ze Slunce na jeden m2 Venuše je ФV = 2610W,
- na jeden m2 Jupitera je ФJ = 50W.
18.Hvězda má zdánlivou magnitudu m1 = 4. Jaká by byla zdánlivá magnituda m2 této hvězdy, kdyby byla ve dvojnásobné vzdálenosti od nás?
Řešení:
Rozbor:
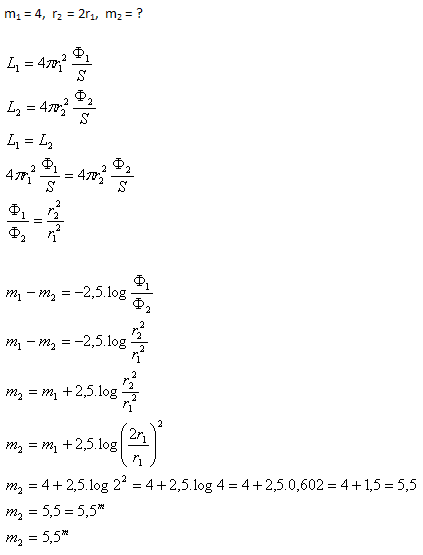
Při dvojnásobné vzdálenosti by zdánlivá magnituda hvězdy byla 5,5m.
19.Uvažujme o vzdálené galaxii, která se od naší Galaxie vzdaluje rychlostí v = 6000 km.s-1. Jakou vlnovou délku spektrální čáry vodíku změříme, je-li její původní vlnová délka 656,3 nm? V jaké vzdálenosti od nás se tato galaxie pravděpodobně nachází?
Řešení:
Rozbor:
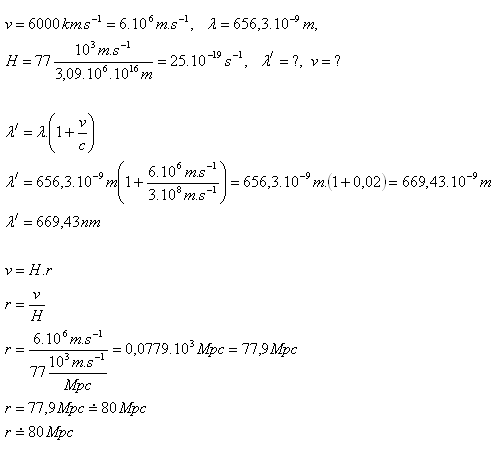
Vlnová délka se zvětší na hodnotu λ/ = 669,43nm. Galaxie je od nás vzdálena asi 80 Mpc.
20.Určete dobu, po kterou se náš vesmír rozpíná. Určete čas, který uplynul od „velkého třesku“ do současnosti.
Řešení:
Rozbor:
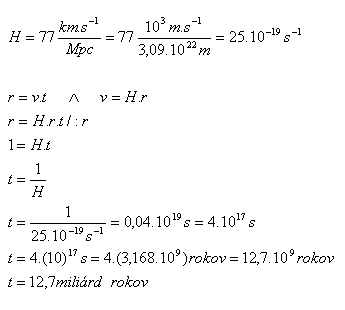
Od „velkého třesku“ uplynulo asi 13 miliard let. Výpočet závisí na volbě Hubbleovy konstanty H.
Pro H platí: 16,13.10–19s-1 < 25.10-19s-1 < 32,26.10–19s-1.