Elektromagnetický oscilátor
1. Uveďte složení a vlastnosti elektromagnetického oscilátoru.
Řešení:
Elektromagnetický oscilátor je obvod střídavého proudu s cívkou (indukčnost) a s kondenzátorem (kapacita). Nazývá se také oscilační obvod nebo obvod LC. V oscilačním obvodu se periodicky přeměňuje elektrická energie na magnetickou energii a naopak. V oscilačním obvodu vzniká elektromagnetické kmitání. Pro frekvenci elektromagnetického oscilátoru (vlastní kmitání oscilátoru) platí Thomsonův vztah:

2.Jak se bude měnit frekvence kmitání oscilačního obvodu, když budeme desky kondenzátoru v oscilačním obvodu vzájemně přibližovat?
Řešení:
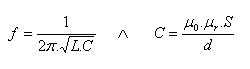
Pokud budeme desky kondenzátoru v oscilačním obvodu vzájemně přibližovat, d se bude zmenšovat, C zvětšovat a frekvence f se bude zmenšovat.
3.Oscilační obvody mají parametry:
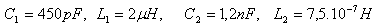
Který obvod kmitá s vyšší frekvencí?
Řešení:
Rozbor:
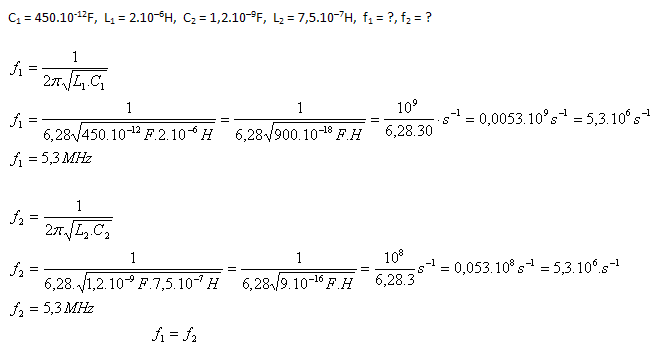
Oba oscilační obvody kmitají se stejnými frekvencemi f1 = f2 = 6,3 MHz.
4.Oscilační obvod tvoří kondenzátor s kapacitou C = 10μF a cívka s proměnnou indukčností. V jakém intervalu se musí měnit indukčnost cívky, aby se frekvence vlastního kmitání oscilačního obvodu měnila v intervalu od 400Hz do 500Hz?
Řešení:
Rozbor:

Indukčnost cívky se musí měnit od L1 = 16mH do L2 = 10mH.
5.Oscilační obvod se skládá z cívky s indukčností L = 3mH a deskového kondenzátoru, jehož desky mají tvar disků s poloměrem 1,2cm. Vzájemná vzdálenost desek je 0,3mm. Určete periodu oscilačního obvodu. Jak se změní perioda obvodu, pokud mezi desky kondenzátoru vložíme dielektrikum s εr = 4?
Řešení:
Rozbor:
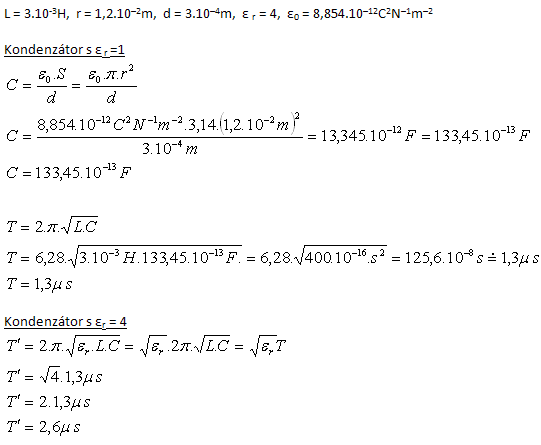
Pokud mezi desky kondenzátoru vložíme dielektrikum s εr = 4, perioda obvodu se zdvojnásobí.
6.K cívce se stálou indukčností L připojíme kondenzátor s kapacitou C1. Zjistíme, že oscilátor kmitá s vlastní frekvencí f1 = 100kHz. Pokud připojíme k této cívce kondenzátor s kapacitou C2, bude oscilátor kmitat s vlastní frekvencí f2 = 160kHz. Jakou vlastní frekvenci bude mít oscilátor, pokud k cívce připojíme oba kondenzátory spojené
Řešení:
Rozbor:
f1 = 100kHz = 105s-1, f2 = 160kHz = 1,6·105s-1
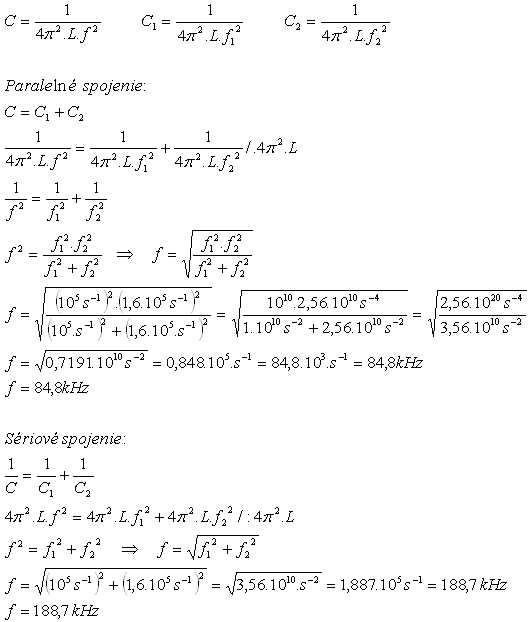
7.Napětí na deskách kondenzátoru v oscilačním obvodu se mění podle rovnice u = 50cos (104π·t) (V). Kapacita kondenzátoru je C = 0,1μF. Vypočítejte periodu kmitání obvodu T a napište rovnici pro okamžitou hodnotu proudu.
Řešení:
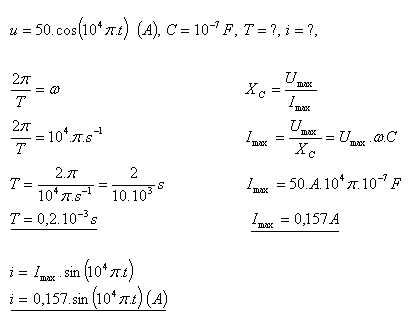
- Perioda kmitání obvodu je T = 0,2·10–3s.
Rovnice pro okamžitou hodnotu proudu je i = 0,157sin (104π·t) (A) .
8.Oscilační obvod tvoří kondenzátor s kapacitou C = 24nF a cívka s indukčností L = 0,6H. V počátečním okamžiku je kondenzátor nabit na napětí Umax = 50V. Napište rovnici pro okamžitou hodnotu proudu v obvodu.
Řešení:
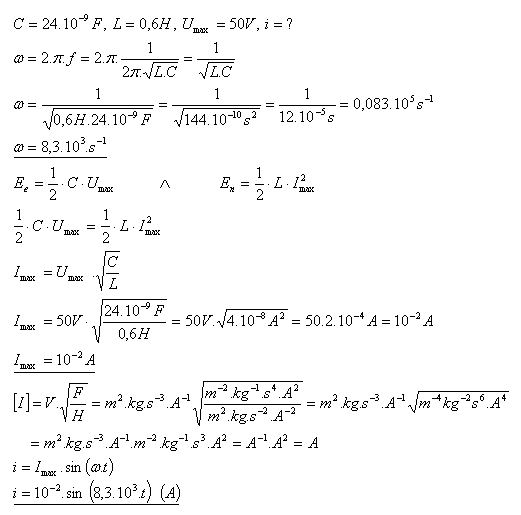
9.Okamžitá hodnota proudu v oscilačním obvodu je dána rovnicí i = 0,01·sin (ω t) (A). Vypočítejte energii magnetického pole cívky pro čas t = T/8 s. V oscilačním okruhu je zapojena cívka s indukčností
L = 0,6H.
Řešení:
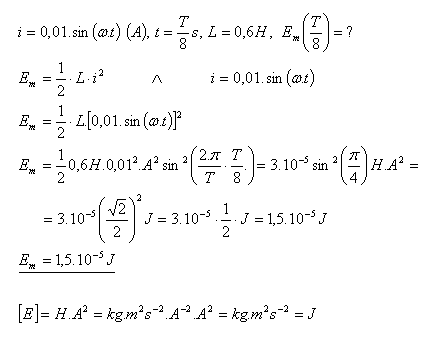
Energie magnetického pole cívky je Em = 1,5·10–5J.
10.Okamžitá hodnota napětí v oscilačním obvodu je dána rovnicí u = 50·cos (ω·t) (V). Vypočítejte energii elektrického pole kondenzátoru s kapacitou C = 24nF pro čas t = T/8 s.
Řešení:
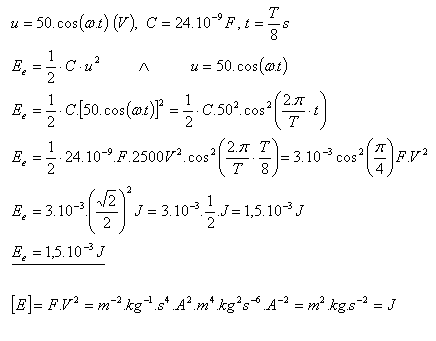
Energie elektrického pole kondenzátoru je Ee = 1,5·10–3J.
11.Oscilační obvod, ve kterém je zapojena cívka (L) a deskový kondenzátor (C1), se vzdáleností desek
d1 = 4,8 mm, je naladěn na vlnovou délku λ1 = 300m. Jak je třeba změnit vzdálenost mezi deskami kondenzátoru, aby oscilační obvod byl naladěn na vlnovou délku λ2 = 240m?
Řešení:
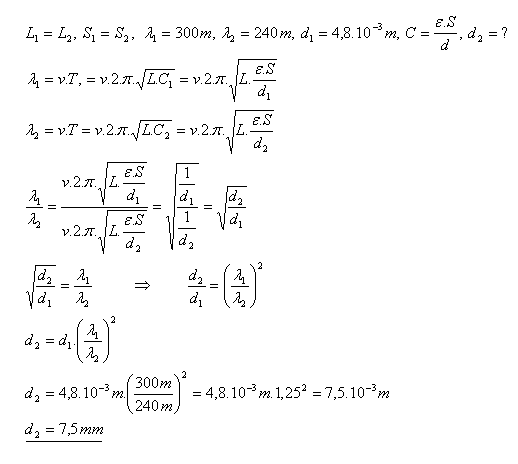
Vzdálenost mezi deskami kondenzátoru je třeba zvětšit na 7,5mm.
12.Kapacita kondenzátorů oscilačního obvodu rozhlasového přijímače se může měnit od C1 = C do C2 = 9C. Určete rozsah vlnových délek přijímače, pokud minimální kapacitě C1 kondenzátoru odpovídá λ1 = 3m.
(L1 = L2 = L)
Řešení:
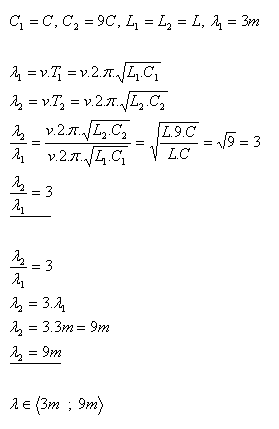
Rozsah vlnových délek přijímače je od 3m do 9m.
13. Oscilační obvod, jehož kapacita je C = 4μF, má frekvenci f1 = 200Hz. Pokud ke kondenzátoru paralelně připojíme další kondenzátor s kapacitou Cx, klesne vlastní frekvence na f2 = 100Hz. Vypočítejte kapacitu přidaného kondenzátoru Cx.
Řešení:
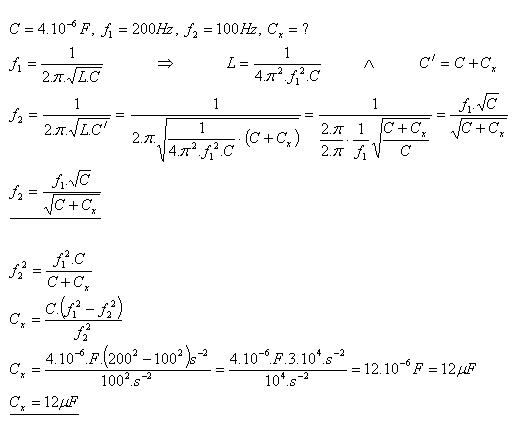
Kapacita přidaného kondenzátoru je Cx = 12μF.
14.V oscilačním obvodu jsou zapojeny sériově kondenzátor (C = 0,01μF), cívka (L = 0,1H) a rezistor (R = 1000Ώ). Jaký je poměr frekvencí obvodu s odporem a bez odporu.
C = 10-8F, L = 10-1H, R = 103Ώ, f1 = ?, f2 = ?
Řešení:
Bez odporu: S odporem: