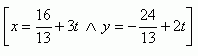Přímka a Kuželosečka
1. Co víte o vzájemné poloze přímky a kuželosečky
Řešení:
Vzájemná poloha přímky a kuželosečky se zjistí řešením soustavy jejich rovnic, které vede na řešení kvadratické rovnice. Pokud
D > 0 přímka je sečnice
D = 0 přímka je tečna
D < 0 přímka je nesečnice
Pokudbod T[ xT; yT] je bod dotyku ležící na kuželosečky i přímce platí:
Rovnice tečen:
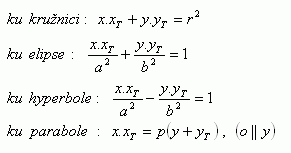
2. Zjistěte vzájemnou polohu přímky 2x +y – 8 = 0 a paraboly x2 +8y = 0
Řešení:
3.Zjistěte vzájemnou polohu přímky x + y – 10 = 0 a elipsy x2 + 3y2 – 3 = 0
Řešení:
4.Vyšetřete vzájemnou polohu kružnice k: x2 + y2 -25 = 0 a přímkp:
Řešení:
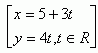
5.Určete c tak, aby přímka x – y + c = 0 byla tečnou paraboly y2 = 6x
Řešení:
6. Určitě k tak, aby přímka y = kx + 3 byla tečnou k hyperbole 16x2 – 25y2 - 400 = 0
Řešení:
7. Napište rovnice tečen ke kružnici x2 + y2 = 25 v jejím dotykovém bodě T [3;y]. Zjistěte také úhel φ mezi tečnou.
Řešení:
8.Napište rovnici tečny k parabole y2 = 18x, která je rovnoběžná s přímkou p : 3x – 4y + 69 = 0
Řešení:
Bod dotyku T [xT ; yT] :
9.Určitě délku tětiv, které postupně porážet kružnice na souřadnicových osách, pokud rovnice kružnice je x2 + y2 – 8x + 7y +12 = 0
Řešení:
Průsečíky s osou x ( y = 0 ):
Průsečíky s osou y ( x = 0):
10.Která tečna elipsy E: x2 + 4y2 -16 = 0 je rovnoběžná s přímkou p:
Řešení:
