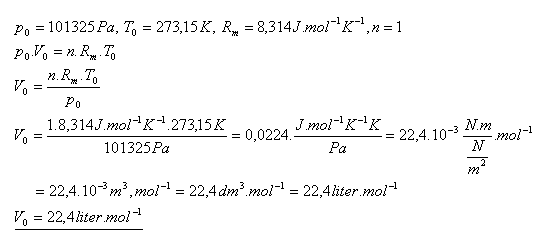Stavová rovnice
1. Jaký je vztah mezi tlakem, objemem a teplotou ideálního plynu?
Řešení:
Stav ideálního plynu, který je v termodynamické rovnováze popisují tři stavové veličiny: tlak p, objem V a termodynamická teplota T. Vzájemný vztah mezi těmito stavovými veličinami vyjadřuje stavová rovnice ideálního plynu.
Stavová rovnice ideálního plynu:
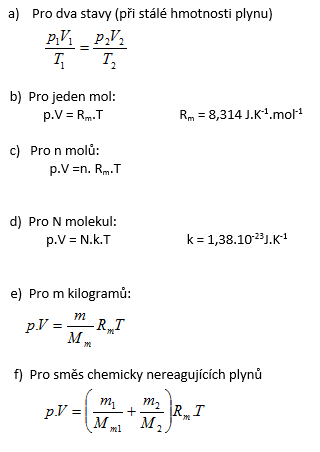
2.Odvoďte číselnou hodnotu a rozměr mollové plynové konstanty Rm.
Řešení:
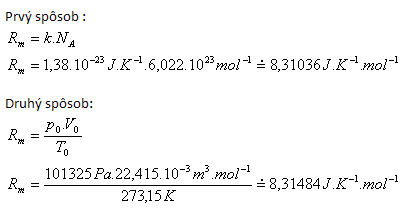
Tabulková hodnota Rm = 3,31441J.K-1.mol-1.
Rozdíly jsou způsobeny různým zaokrouhlením vstupních hodnot.
3.Zjistěte kolik molekul obsahuje 1 cm3 libovolného plynu za normálních podmínek.
Řešení:
Rozbor:
V = 1 cm3 = 10-6m3, p = 101325 Pa, T = 273,15 K
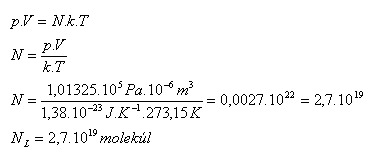
Jeden cm3 libovolného plynu za normálních podmínek obsahuje NL = 2,7.1019 molekul. Je to Loschmidtovo číslo. (Jozef Loschmidt 1821-1895)
4. V nádobě s vnitřním objemem 8,3 m3 je vodík H2 s hmotností 200 ga teplotou 27oC. Určete jeho tlak!
Řešení:
Rozbor:
V = 8,3 m3, m = 200 g = 0,2 kg, t = 27oC, T = (27 +273,15) K= 300,15 K
Mm = 2.1.10-3kg.mol-1, Rm = 8,314 J.K-1.mol-1
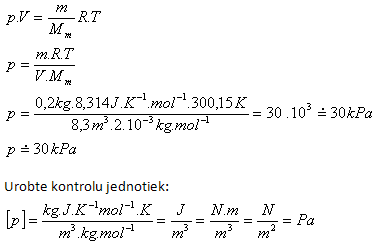
V nádobě je tlak asi 30 kPa.
5.V nádobě s vnitřním objemem 5.10-3m3 je uzavřen dusík N2 pri teplotě 39oC a tlaku 1,6.105Pa. Určete jeho hmotnost.
Řešení:
Rozbor:
V = 5.10-3m3, p =1,6.105Pa, T = 312,15 K, Rm = 8,314 J.K-1.mol-1
Mm = 2.14.10-3kg.mol-1
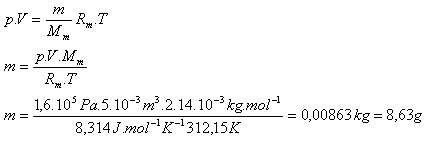
Hmotnost dusíku je m = 8,63 g
6.Jaký tlak má vzduch v pneumatice nákladního auta při teplotě 20oC a hustotě 8kg.m-3. Mm(vzduch) = 29.10-3kg.mol-1
Řešení:
Rozbor:
T = 293,15 K, ρ = 8kg.m-3, Mm(vzduch) = 29.10-3kg.mol-1
Rm = 8,314 J.K-1.mol-1
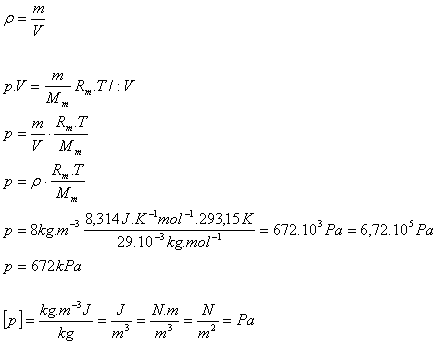
Tlak vzduchu v pneumatice je p = 672 kPa.
7.Kolik molekul je v kulaté nádobě s vnitřním poloměrem 3 cm, naplněné kyslíkem O2, který má teplotu 27oC a tlak 1,36.10-2Pa.
Řešení:
Rozbor:
r = 3 cm = 3.10-2m, T = 300,15K, p = 1,36.10-2Pa
k = 1,38.10-23J.K-1, V = 4/3π.r3, N = ?
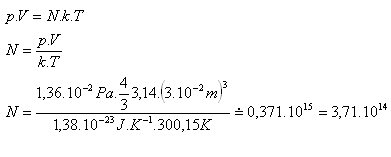
V nádobě je N = 3,71.1014 molekul kyslíku O2
8.V nádobě je dusík N2 s hmotností 10 kg při tlaku 10 MPa. Určitě hmotnost dusíku, který je třeba vypustit z nádoby, aby se jeho tlak zmenšil na 2,5 MPa. (Teplota dusíku se nemění)
Řešení:
Rozbor:
m1 = 10 kg, p1 = 107Pa, p2 = 2,5.106Pa, T = konstanta
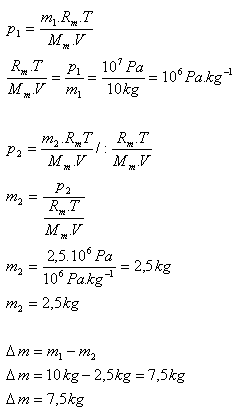
Z nádoby je třeba vypustit 7,5 kg dusíku.
9.Hustota dusíku za normálních podmínek (T1 = 273,15 K a p1 = 101325 Pa) je ρ1 = 1,23 kg.m-3. Určete hustotu dusíku při teplotě 30oC a normálního tlaku.
Řešení:
Rozbor:
T1 = 273,15 K, T2 = 303,15 K p1 = p2 = 101325 Pa, ρ1 = 1,23 kg.m-3, ρ2 = ?
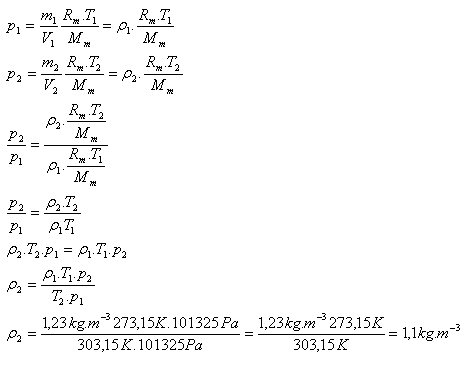
Hustota dusíku při teplotě 30oC a za normálního tlaku je 1,1 kg.m-3.
10. Vypočtěte efektivní Molární hmotnost vzduchu Mm. Vzduch považujeme za směs 75% dusíku a 25% kyslíku.
Řešení:
Rozbor:
Mm(N2) = 28.10-3kg.mol-1, m1(N2) = 0,75m
Mm(O2) = 32.10-3kg,mol-1, m2O2) = 0,25m
m = celková hmotnost vzduchu
Efektivní Molární hmotnost (platí pro dva chemicky nereagující plyny)
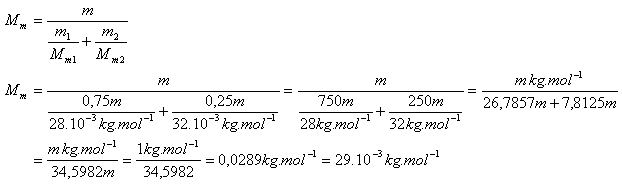
Efektivní Molární hmotnost vzduchu je Mm = 29.10-3.mol-1
11.Ideální plyn uzavřený v nádobě s vnitřním objemem 2,5 litru má teplotu -13,150 C. Jaký je jeho tlak, pokud v plynu je 1024 molekul?
Řešení:
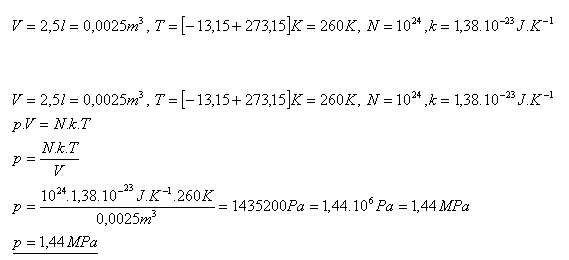
Tlak plynu je 1,44 MPa.
12.Určete objem oxidu uhličitého CO2 o hmotnosti 1 gram při teplotě 210C a tlaku 1,0 kPa.
Řešení:
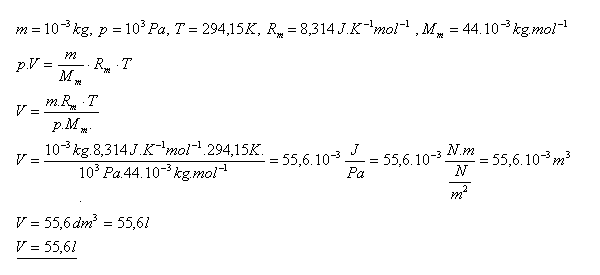
Objem oxidu uhličitého CO2 je 55,6 litra.
13.Kolik molekul je obsaženo v nádobě s plynem, která má vnitřní objem 1 litr, pokud plyn má teplotu 100C a tlak 0,2 MPa?
Řešení:
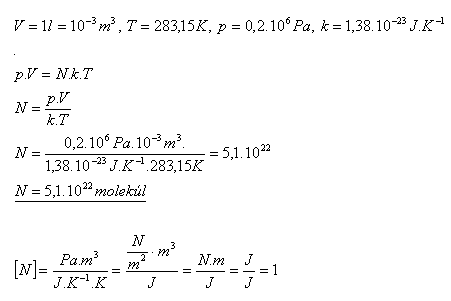
V nádobě je 5,1.1022 molekul.
14.Ideální plyn uzavřený v nádobě má objem 1,3 m3 a teplotu -13,150 C. Jaký je tlak tohoto plynu, pokud jeho látkové množství je 4 kilomoly?
Řešení:
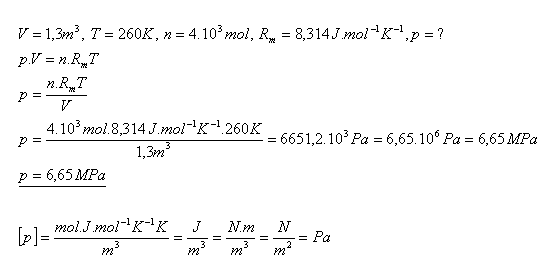
Tlak ideálního plynu je 6,65 MPa.
15.Určete objem kyslíku O2 o hmotnosti 8 gramů při teplotě 210C a tlaku 1,4.105 Pa.
Řešení:
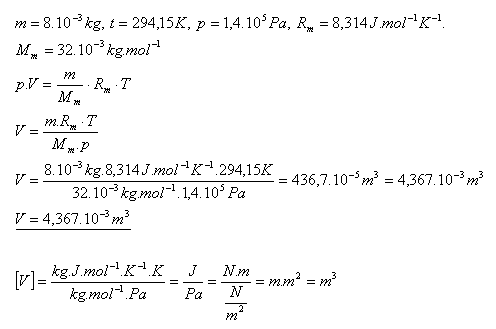
Objem kyslíku je 4,367.10-3m3.
16.V nádobě s objemem 5.10-3m3 je uzavěn dusík N2 při teplotě 390C a tlaku 1,6.105Pa. Určete hmotnost dusíka.
Řešení:
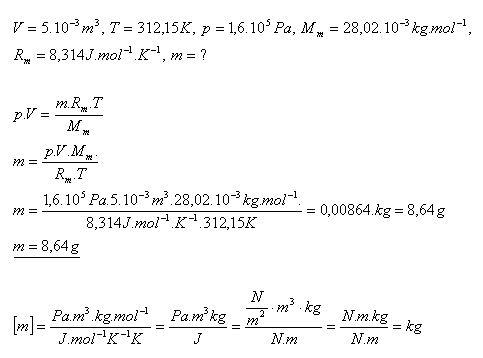
Hmotnost dusíku N2 je 8,64 gramov.
17.Určete molární hmotnost plynu, který má při teploté 00C a tlaku 100 kPa hustotu 1,95 kg.m-3. O který plyn se jedná?
Řešení:
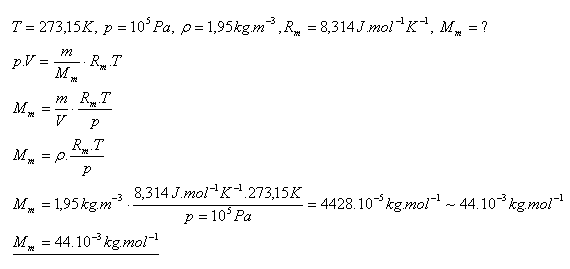
Je to oxid uhličitý CO2.
18.Hustota vzduchu při normálních podmínkách je 1,27 kg.m-3. Určete hustotu vzduchu při teplotě 300C a normálním tlaku.
Řešení:
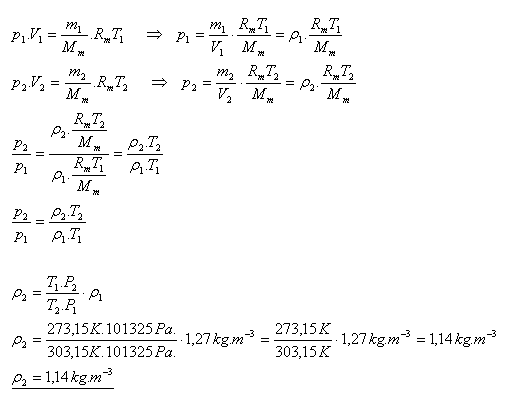
Hustota vzduchu při teplotě 300C a normálním tlaku je 1,14 kg.m-3.
19.Jak se změní objem ideálního plynu, když se jeho termodynamická teplota zvětší dvakrát a tlak se zvýší o 25%.
Řešení:
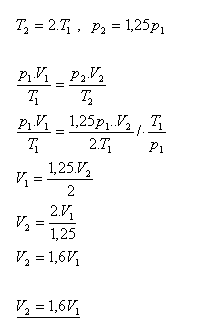
Objem ideálního plynu se zvětší 1,6 krát.
20.Ukažte, že libovolný ideální plyn má při normálních podmínkách ( p0 = 101325 Pa, T0 = 273,15 K ) stejný molární objem V0 = 22,4 litr.mol-1.
Řešení: