Tepelná roztažnost
1. Charakterizujte - tepelnou roztažnost pevných, kapalných a plynných látek!
Řešení:
Tepelná roztažnost je změna rozměrů tělesa zapříčiněna změnou jeho teploty.

2.Měděný drát (α = 1,7.10-5K-1) měl při teplotě-50C délku 21,55 m.. Jakou délku má při teplotě 300C. O kolik cm se drát prodloužil?
Řešení:
Rozbor:
l0 = 21,55m, α = 1,7.10-5K-1= 0,000017K-1, Δt = 300C-(-50C) = 350C
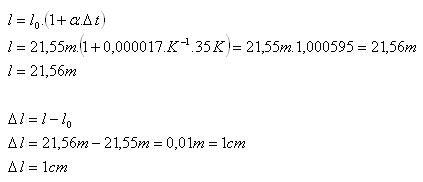
Drát po zahřátí má délku 21,56 m.. Prodloužil se o 1 cm.
3.Měděný drát (α = 1,7.10-5K-1), jehož délka při teplotě 180C byla 150 cm, zahřál se při průchodu elektrickým proudem a prodloužil se o 9 mm. Na jakou teplotu byl drát ohřátý?
Řešení:
Rozbor:
l0 = 150 cm =1,5 m, t1 = 180C, Δ l = 0,009 m, α = 1,7.10-5K-1
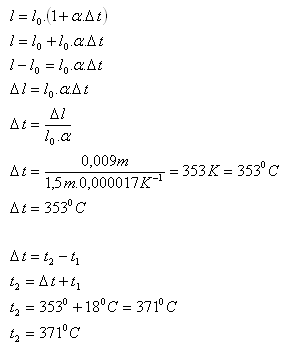
Drát byl zahřátý na teplotu 3710C
4.Dvě tyče, železná (α1 = 1,2.10-5K-1) a zinková (α2 = 2,9.10-5K-1) měli při teplotě 00C stejnou délku. Když zvýšíme jejich teplotu na 1000C je rozdíl jejich délek 1 cm. Jaké byly jejich původní délky?
Řešení:
Rozbor:
α1 = 1,2.10-5K-1, α2 = 2,9.10-5K-1, Δt = 100 K, Δl = 0,01m

Původní délky tyčí byly l0 = 5,88 m.
5.Hliníková nádoba (α (Al) = 24.10-6K-1) při teplotě 200C vnitřní objem 10 litrů. Jak se změní její vnitřní objem při teplotě 1000C?
Řešení:
Rozbor:
α (Al) = 24.10-6K-1, t1 = 200C, t2 = 1000C, Δt = 800C = 80 K,
V0 = 10 l = 10 dm3 = 10-2m3
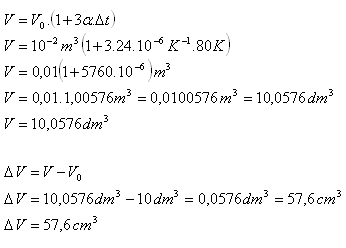
Vnitřní objem nádoby se zvětší o 57,6 cm3
6.V tabulkách je uvedeno, že měď má při teplotě 200C hustotu ρ20= 8930 kg.m-3. Jaká je hustota mědi při teplotě 800C?
Řešení:
Rozbor:
ρ20 = 8930 kg.m-3, t1 = 200C, t2 = 800C, Δt =600C = 60 K, α(Cu) = 1,7.10-5K-1
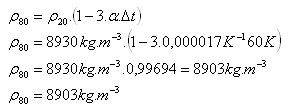
Hustota mědi při teplotě 800C je ρ80 = 8903 kg.m-3.
7.Podlahová dlaždice je z mramoru (α = 0,85.10-5K-1) a má tvar čtverce. Strana dlaždice má při teplotě 00C délku 0,5 m.. O kolik cm2 se zvětší plošný obsah dlaždice, pokud se její teplota zvýší na 350C?
Řešení:
Rozbor:
α = 0,85.10-5K-1, a0 = 0,5 m, Δt = 350C, ΔS = ?
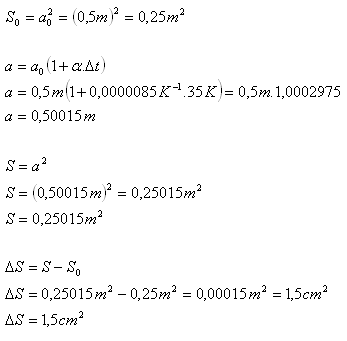
Plošný obsah dlaždice se zvětší o 1,5 cm2
8.Mosazná koule (α = 1,8.10-1K-1) má při teplotě 150C poloměr r1 = 2 cm. O kolik 0C ji třeba ohřát, aby neprošla kruhovým otvorem o poloměru r2 = 2,02 cm?
Řešení:
Rozbor:
α = 1,8.10-1K-1, r1 = 2 cm, r2 = 2,02 cm,
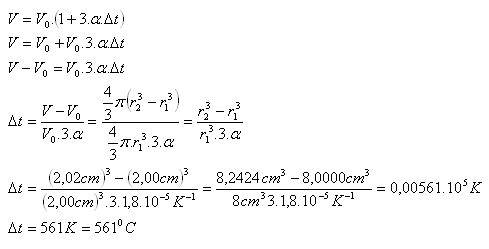
Mosaznou kouli třeba ohřát o 5610C na 5760C
9.Cisternový vagón je až po otvor naplněný naftou. (ρ = 940 kg.m-3, β = 1.10-3K-1). Při teplotě 00C se do vagonu vejde 50 tun nafty. Kolik nafty vyteče otvorem z vagónu, pokud po cestě se teplota nafty zvýší na 200C?
Řešení:
Rozbor:
ρo = 940 kg.m-3, β = 1.10-3K-1, m0 = 50 000 kg, Δt = 200C = 20 K
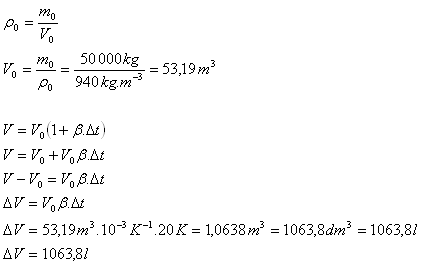
Z vagónu vyteče 1063,8 litra nafty.
10. Vzduch v nádobě s pohyblivým pístem má při teplotě 100C objem 1 litr. Jaký je objem vzduchu při teplotě 400C? Vypočtěte také relativní změnu objemu vzduchu!
Řešení:
Rozbor:
V0 = 1 l = 1 dm3 = 1000 cm3, Δt = 300C = 30 K,
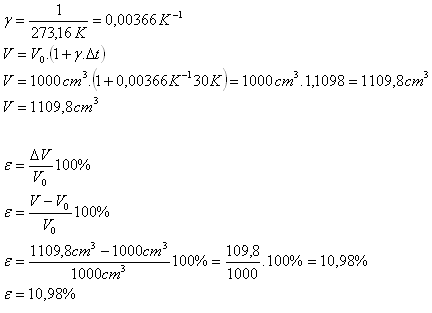
- Objem vzduchu při teplotě 400C je V = 1109,8 cm3.
- Relativní změnu objemu vzduchu je ε = 10,98%.
11.Žák Omylný tvrdil, že ze vztahu l = l0. (1 + α.Δt) vyplývá, že při dostatečně velkém ochlazení bude délka tyče "l" nulová. Může mít pravdu? S kterým důležitým přírodním zákonům je toto tvrzení v rozporu?
Řešení:
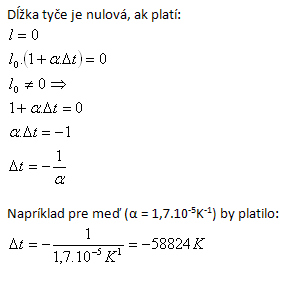
Měděnou tyč by bylo třeba ochladit o 58824 K. Takto nízká teplota ve vesmíru neexistuje. Nejnižší možná teplota (dosud nedosažená) je 0K = -273,150C. – Absolutní nula
12.Potrubí teplovodu délky 200 m bylo svařované při teplotě 200C. O jakou délku se prodlouží, pokud v provozních podmínkách teplota naroste na 1200C.
Řešení:
Rozbor:

Potrubí teplovodu se prodlouží o 24 centimetrů.
13.Při teplotě 100C má měděná kostka objem 600 cm3. Jak se změní její objem po zahřátí na 2100C?
Řešení:
Rozbor:

Objem kostky se zvětší o 6,156 cm3.
14.Vypočítejte součinitel objemové tepelné roztažnosti benzínu, který při teplotě 300C má objěm 10,3.10-3m3 a při teplotě 00C objem 10-2m3.
Řešení:
Rozbor:
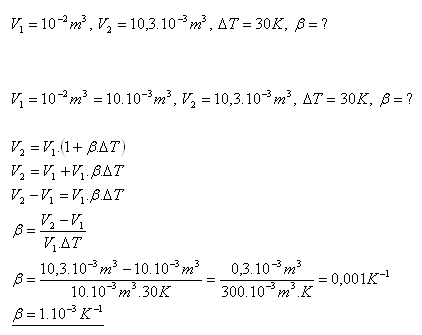
Součinitel objemové tepelné roztažnosti benzínu je 1.10-3K-1.
15. Vypočtěte hmotnost 1dm3 mědi při teplotě 4000C, když při teplotě 00C je hustota mědi je 8,9.103kg.m-3.
Řešení:
Rozbor:

Hmotnost mědi je 8,72 kg.
16.Při 00C má zinková tyčka délku 200 mm a měděná 201 mm. Jejich příčné rozměry při 00C jsou stejné. Vypočítejte při jaké teplotě mají tyčky stejný objem.
Řešení:
Rozbor:

Tyčky budou mít stejný objem při teplotě 1290C.
17.Ocelová koule má při teplotě 800C poloměr 2cm. Jaký je objem této koule při teplotě -200C?
Řešení:
Rozbor:
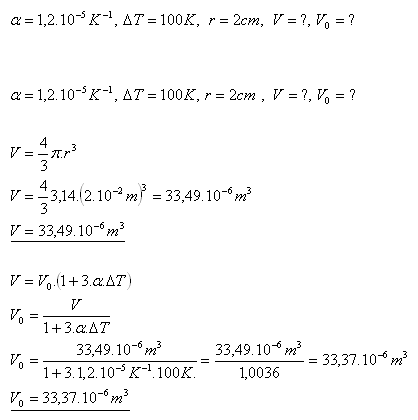
Objem koule při teplotě – 200C je 33,37 cm3.
18.Jaké teplo přijme měděná tyč, která má při teplotě 200C délku 10cm a průřez 2cm2, pokud se při zahřátí prodlouží o 0,1 mm.
Řešení:
Rozbor:
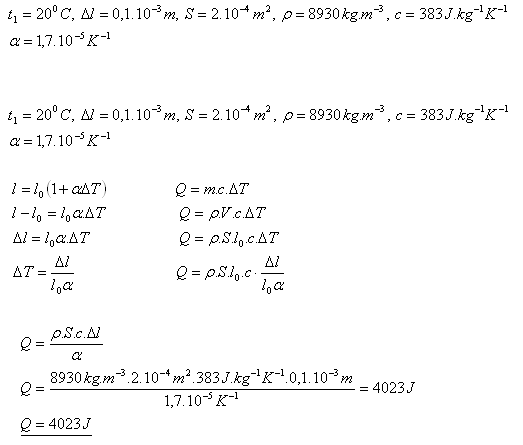
Meděná tyč přijala 4023 J tepla.
19.Na tenkém ocelovém drátku kmitá kulička s dobou kmitu 2 sekundy. Délka závěsu při teplotě 200C je 2 metry. Jak se změní doba kmitu, pokud kyvadlo zahřejeme na 800C?
Řešení:
Rozbor:
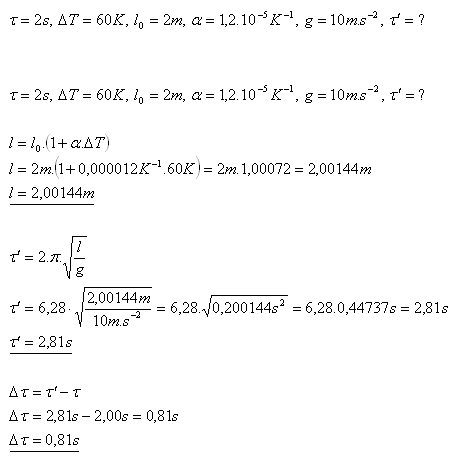
Po ohřátí se doba kmitu zvětší o 0,81 sekundy.
20.O kolik se prodlouží hliníkový drát průřezu 5 mm2, kterým za 1 minutu prochází elektrický proud s výkonem 16 W. (Tepelné ztráty zanedbejte)
Řešení:
Rozbor:
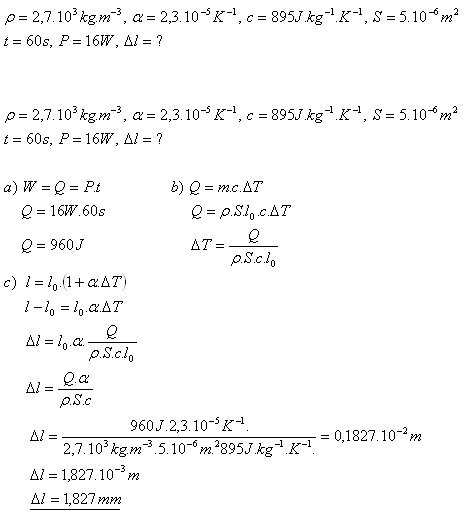
Drát se prodlouží o 1,827 mm.