Aritmetická posloupnost
1.Charakterizujte vlastnosti aritmetické posloupnosti.
Posloupnost (a2)∞n+1 je aritmetická právě tehdy, pokud existuje d є R, že pro všechny n є N platí
an+1 = an + d . Číslo d se nazývá diference aritmetické posloupnosti.
V aritmetické posloupnostii platí:
- an = a1 + (n-1)d
- ar = as + (r-s)d
- s = a1 + a2 + a3 + ... + an =
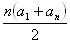
- Ak d > 0 je posloupnost rostoucí
- Ak d < 0 je posloupnost klesající
- Ak d = 0 je posloupnost konstantní
2.Zjistěte, zda je posloupnost aritmetická:
Řešení:
a1 = -2, a2 = -1, a3 = 0, a4 = 1, a5 = 2 atď.
Posloupnost je aritmetická s diferencí d = 1.
3.Napište prvních šest členů aritmetické posloupnosti pro kterou platí:
a1 + a4 + a6 = 71
a5 – a2 – a3 = 2
Řešení:
a1 + a1 +3d +a1 +5d = 71
a1 + 4d – a1-d –a1 -2d = 2
3a1 + 8d = 71
-a1 + d =2/3
3a1 + 8d = 71
-3a1 + 3d = 6
a1 – d = -2
a1 = d - 2
a1 = 7 - 2
a1 = 5
11d = 77
d = 7
(a2)n-16 = 5;12;19;26;33;40
4.Napište prvních šest členů aritmetické posloupnosti pro kterou platí:
Řešení:
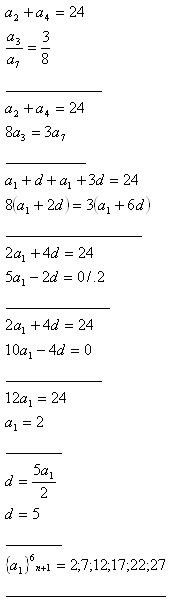
5.Osm čísel tvoří aritmetickou posloupnost. Určitě je, pokud víte, že součet prostředních členů je 41, součin krajních je 114.
Řešení:

6.Mezi kořeny kvadratické rovnice x2 - 16x +39 = 0 vložte čtyři čísla, aby spolu tvořily aritmetickou posloupnost.
Řešení:
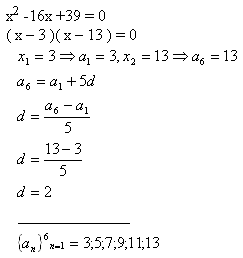
Vložené čísla jsou: 5;7;9;11
7.Strany pravoúhlého trojúhelníku tvoří aritmetickou posloupnost. Delší odvěsna má 24 cm. Vypočítejte obvod trojúhelníku.
Řešení:
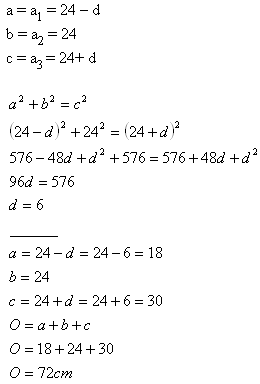
Obvod trojúhelníka je 72 cm.
8.Zjistěte součet přirozených čísiel 1+2+3+4+5+6+7+.............+100.
Řešení:
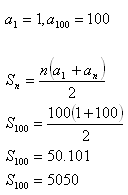
Součet daných čísiel je S = 5050.
9.Železné trubky jsou srovnané do osmi řad tak, že vrchní řada má 13 trubek a každý další o troubu víc. Kolik je všech trubek?
Řešení:
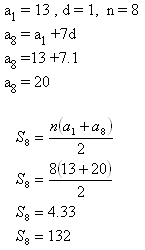
Na hromadě je 132 trubek.
10.V trojúhelníku úhly tvoří aritmetickou posloupnost. Určete ostatní úhly, pokud nejmenší úhel má velikost 20°.
Řešení:
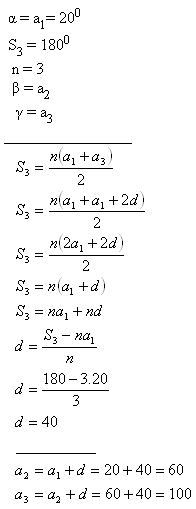
Úhly trojúhelníku jsou 20°, 60° a 100°.
11.Hrany kvádru tvoří tři po sobě jdoucí členy aritmetické posloupnosti. Jaké jsou velké, pokud jejich součet je 24 cm a objem kvádru je 312 cm3?
Řešení:
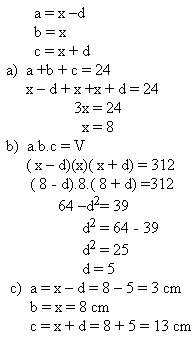
Hrany kvádru mají velikost 3 cm, 8 cm a 13cm.
12.Jak dlouho by padal kámen do dolu v Jižní Americe hluboké 2500 m, pokud víme, že v první vteřině proletí 4,904 ma za každou další o 9,808 m více?
Řešení:
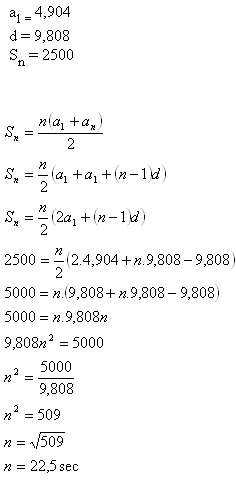
Kámen by do dolu padal asi 22,5 sec.