sk|en|

Fyzika

Dynamika

1.Jak velkou silou působí člověk s hmotností 75 kg na podlahu kabiny výtahu, když

  • a) výtah je v klidu
  • b) výtah se pohybuje svisle vzhůru se zrychlením  a = 2 m.s-2
  • c) výtah se pohybuje svisle dolů se zrychlením  a = 2 m.s-2  (g = 10 m.s-2)

Řešení:

a)    F1 = m.g

F1 = 75 kg.10 m.s-2= 750 kgms-2= 750 N.

 

b) F2 = m.( g + a )

F2 = 75 kg.12m.s-2 = 900 kgms-2 = 900 N

 

c) F3 = m.( g – a )

F3= 75 kg .8 m.s-2 = 600 kgms-2 = 600 N


Působící síly jsou F1 = 750 N, F2 = 900 N, F3 = 600 N .

2.Na elektron v elektrickém poli ve vakuu působí stálá síla F F = 18,2.10-20 N. Jak velkou rychlost získá elektron (me= 9,1.10-31kg), pokud z klidu proběhne dráhu 1cm.

Řešení:

Rozbor:

F = 18,2.10-20 N, m e= 9,1.10-31 kg , s = 1cm = 10–2m.

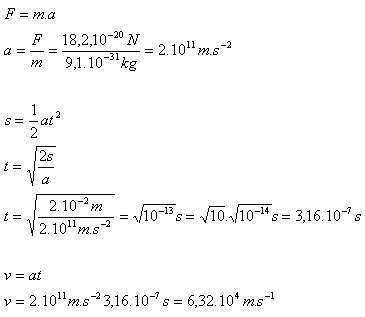
fyzika-dynamika-2 

Elektron získa rychlost v = 6,32.104 m.s-1

3.Letadlo s hmotností 12 t má rychlost 252 km.h-1. Motory působí na letadlo celkovou tahovou silou 20 kN. 30% této síly připadá na překonání tření a odporu vzduchu. Jaká musí být délka startovací dráhy?

Řešení:

Rozbor :

m = 12 t = 12 000 kg, v = 252 km.h-1 = 70 m.s-1,

F = 70% ze 20 000 N = 0,7.20 000 N = 14 000 N

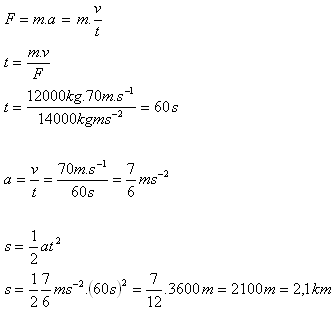
fyzika-dynamika-3

Délka startovací dráhy musí být minimálně 2,1 km.

4.a) Uveďte vzorce pro výpočet velikosti odstředivé (dostředivá) síly.

b) Jak velká dostředivá síla působí na kuličku o hmotnosti 200 g upevněnou na niti, pokud kulička koná rovnoměrný pohyb po kružnici ve vodorovném směru. Délka nitě je 60 cm, rýchlosť 6m.s-1

Řešení:

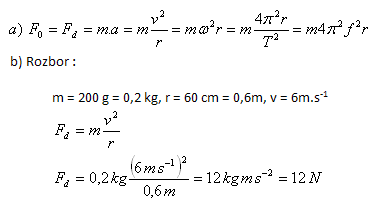
fyzika-dynamika-4

Na kuličku působí dostředivá síla 12 N.

5.Při akrobatickém letu popisuje letadlo rychlostí 360 km.h-1 kružnici o poloměru 400 mv svislé poloze. Jak velkou tlakovou silou působí letec s hmotností 80 kg na sedadlo v nejvyšším a nejnižším bodě trajektorie?

Řešení:

Rozbor:

v = 360 km.h-1 = 100 m.s-1, r = 400 m, m = 80 kg, g = 10 m.s-1

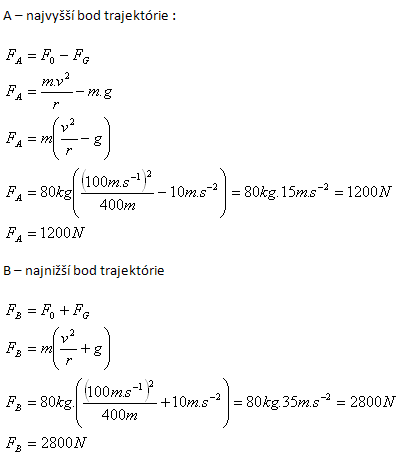
fyzika-dynamika-5
 

Letec působí na sedadlo silou FA = 1200 N nebo FB = 2800 N

6.Automobil o hmotnosti 1 000 kg má rychlost 54 km.h-1. Vjel na most s poloměrem křivosti r = 50 m.

  • a) Jak velkou tlakovou silou působil automobil na cestu na vrcholu mostu?   
  • b) Jakou rychlostí se automobil pohybuje na vrcholu mostu   
  • c) Co se stane, pokud je rychlost automobilu 90 km.h -1

Řešení:

Rozbor : m = 1000 kg, v =54 km.h-1=15 m.s-1, r = 50 m, v‘ =90 km.h-1= 25 m.s-1

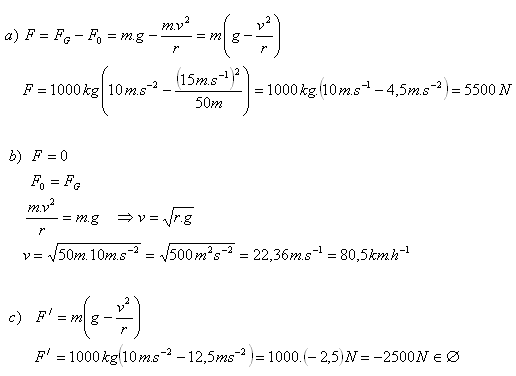
fyzika-dynamika-6 

  • a) F = 5500 N.
  • b) Rychlost je 80,5 km.h-1.
  • c) Při rychlosti 90 km.h-1 nastane skok automobilu. Automobil přejde do šikmého vrhu.

7.Kolo auta má hmotnost 6 kg. Jeho těžiště je mimo středu tělesa, proto na kolo v místě těžiště působí odstředivá síla F0 = 3,03 N. Jak daleko je těžiště od středu, pokud se kolo otáčí 96 ot / min.

Řešení:

Rozbor :

m = 6 kg, F0 = 3,03 N, f = 96 ot/min = 1,6 s-1

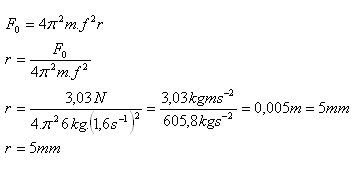
fyzika-dynamika-7

Vzdálenost těžiště od středu je 5 mm.

8.Určiete zrychlení tělesa šmýkajúceho se (bez tření) po nakloněné rovině délky l = 20 m, se stoupáním

α = 5o. Určitě také rychlost tělesa na konci nakloněné roviny.

Řešení:

Rozbor:

l = 20 m, α = 50, g = 10 m.s-3

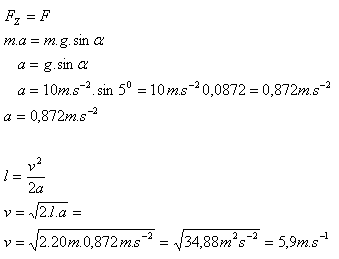
 fyzika-dynamika-8

Zrychlení tělesa je a = 0,872 ms-2.Je rychlost na konci nakloněné roviny je asi 6 ms-1.

9.Jaký je součinitel smykového tření saní o hmotnosti 400 kg, pokud k udržení saní v rovnoměrném pohybu třeba překonat sílu tření FT = 80 N. Zjistěte také jaký náklad dřeva utáhnou koně na těchto sáňkách, pokud jejich tažná síla je F'T = 1400 N.

Řešení:

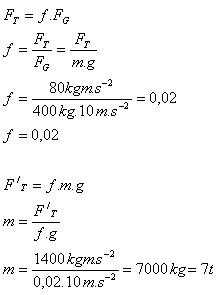
fyzika-dynamika-9 

Hmotnosť nákladu dřeva: 7000-400=6600 kg

Součinitel tření mezi saněmi a sněhem je f = 0,02. Koně utáhnou 6600 kg dřeva.

10.Na nakloněné rovině je kvádr o hmotnosti 5 kg. Nakloněná rovina má sklon α = 30o a součinitel smykového tření f = 0,35. Jakou silou je třeba na těleso působit, aby bylo v klidu?

Riešenie:

Podmínka rovnováhy na nakloněné rovině je:

F = m g( sin α – f cos α )

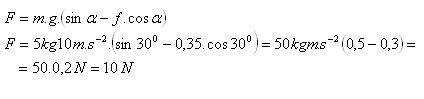
fyzika-dynamika-10 

Na těleso třeba působit silou F = 10 N.

11.Sypaný materiál se skladuje ve skladech na kupách tvaru kužele. Vypočtěte úhel sklonu, který zvíře volně sypaný materiál s vodorovnou rovinou pro

  • a)    uhlí: f = 1
  • b)    hlína: f = 0,8
  • c)    písek: f = 0,68 (f-Součinitel smykového tření)

Řešení:

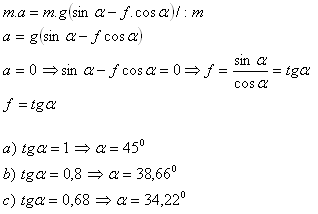
fyzika-dynamika-11 

Úhly sklonu jsou: uhlí α = 450, hlína α = 38,660, písek α = 34,220

12.Dvě tělesa o hmotnostech m1 a m2 jsou upevněny přes kladku na nakloněné rovině. Jaká musí být hmotnost druhého tělesa m2 pokud má udržet v klidu těleso o hmotnosti m1 = 8 kg, když nakloněná rovina má sklon α = 400 a součinitel smykového tření f = 0,4 (g = 10 ms-2)

Řešení:

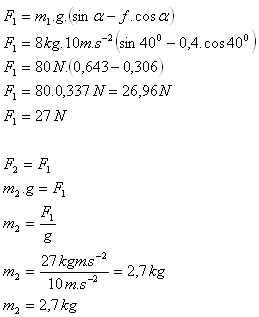
fyzika-dynamika-12 

Hmotnost druhého tělesa je m2 = 2,7 kg.

13.Automobil s hmotností 2 000 kg jde stálou rychlostí do kopce 4% stoupáním. Určitě tažnou sílu motoru.

Řešení:

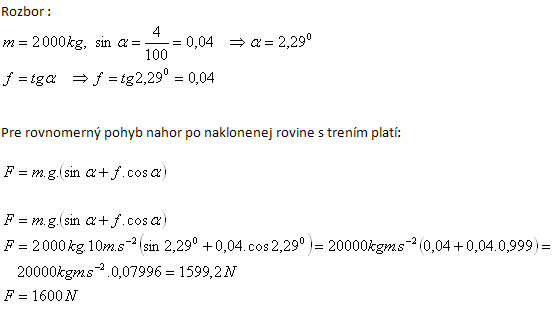
fyzika-dynamika-13 

Tažná síla motoru je 1600 N.

14.Automobil s hmotností 500 kg se rozjíždí do kopce s 2% stoupáním a konstantním zrychlením a = 2 ms-2. Určitě tažnou sílu motoru.

Řešení:

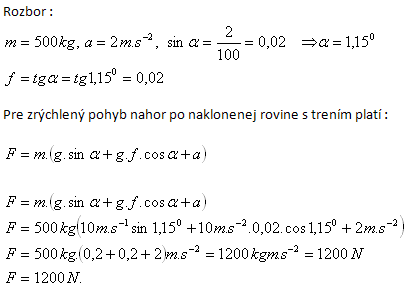
fyzika-dynamika-14 

Tažná síla motoru je 1200 N.

15.Automobil s hmotností 200 kg se rozbíhá do kopce (α = 5o, f = 0,09 ). Jaké je zrychlení automobilu, pokud tažná síla motoru je 653,3 N.

Řešení:

Rozbor.

m = 200 kg, F = 653,3 N. α = 5o, f = 0,09 , FG = 2000 N, a = ?

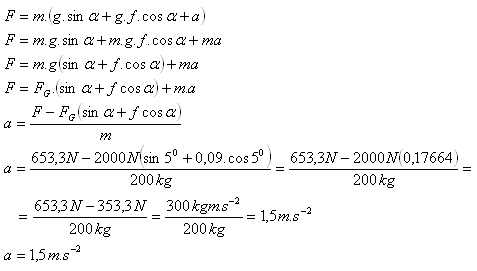
fyzika-dynamika-15 

Zrychlení automobilu je a = 1,5 m.s-2

16.Střela o hmotnosti 10 g je vystřelena rychlostí 800 ms-1 z pušky s hmotností 4 kg. Vypočtěte zpětnou rychlost pušky.

Řešení:

Rozbor :

m 1= 10 g = 0,01 kg, m 2 = 4 kg, v1 = 800 m.s-1, v2 = ?

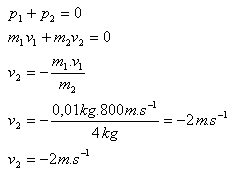
fyzika-dynamika-16

Zpětná rychlost pušky je v2 = 2m.s-1.

17.Samopal vystřelí 600 střel za minutu. Každá střela má hmotnost 4 g, rychlost střely při opouštění hlavně je 500 ms-1. Určitě průměrnou velikost síly, kterou samopal tlačí na rameno střelce.

Řešení:

Rozbor:

600 / min = 600 / 60 s , 1 strela za 60 /600 s = 0,1s. t = 0,1 s.

m1 = 4 g = 0,004 kg, v1 = 500 m.s-1

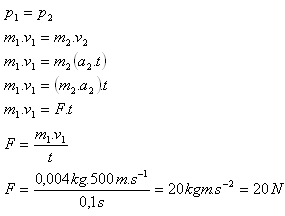
fyzika-dynamika-17 

Samopal tlačí na rameno střelce průměrnou silou F = 20 N.

18.Dvě koule pohybující se stejným směrem se srazí. První má hmotnost 2 kg a pohybuje se rychlostí

2,5 ms-1. Druhá má hmotnost 8 kg. Jakou rychlostí se pohybuje druhá koule, jestliže po srážce se spolu pohybují rychlostí 2,1 ms-1.

Řešení:

Rozbor:

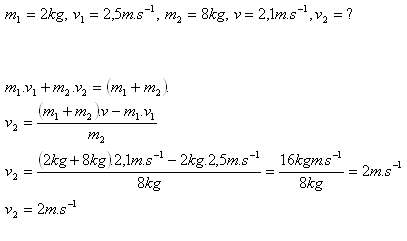
fyzika-dynamika-18 

Druhá koule se pohybovala rychlostí v2 = 2m.s-1.

19.Střela o hmotnosti 100 kg letící podél železniční trati rychlostí 500 ms-1 narazila na vagón s pískem o hmotnosti 10 t a uvízla v něm. Jakou rychlostí se bude vagón po nárazu pohybovat, pokud před srážkou se pohyboval rychlostí 36 km.h-1

  • a) proti střele
  • b) ve směru střely

Řešení:

Rozbor:

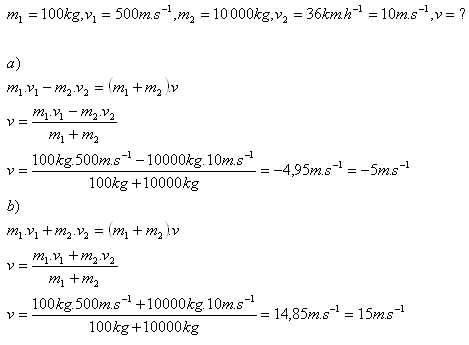
fyzika-dynamika-19

20. Chlapec s hmotností 60 kg stojí na bruslích na hladkém ledě. Do pohybu se uvede tím, že odhodí ledovou kru s hmotností 6 kg rychlostí 3 ms-1. Do jaké vzdálenosti se chlapec odhozením kry dostane, pokud se pohybuje 9 sekund.

Řešení:

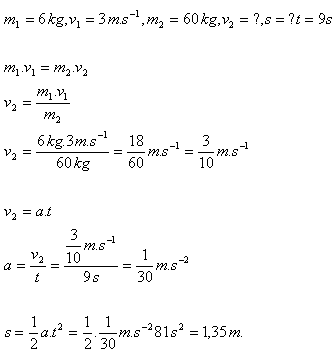
fyzika-dynamika-20 

Bruslař projde dráhu 1,35 m.

21.Jednu etapu cyklistických závodů Okolo Slovenska tvořil krátký sprint do kopce. Cyklisté se pohybovaly po přímé cestě se stoupáním p = 7,5%. Vodorovná vzdálenost mezi startem a cílem je s = 825 m. Vítěz etapy se pohyboval rovnoměrným pohybem a dosahoval během své jízdy průměrný výkon P = 350 W. Hmotnost cyklisty is kolem je m = 68 kg.

  • Za jaký čas t absolvoval vítěz tuto etapu?    
  • Jakou průměrnou rychlostí v průběhu závodu pohyboval?

Řešení:

dynamika-21a

Vítěz absolvuje etapu za 120,45 s, tedy za 2 minuty. Během závodu se pohyboval průměrnou rychlostí 6,87 ms-1, tedy 24,7 km.h-1. 

Toto řešení nám zaslal Jakub Hrdina, děkujeme.