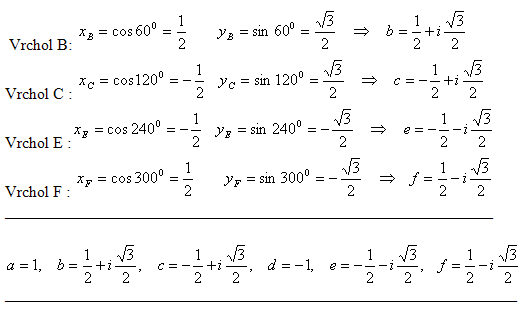Vlastnosti komplexních čísel
1. Jaké vlastnosti mají komplexní čísla?
Řešení:


2.Dané jsou komplexní čísla a = 1 +2 i, b = 2 - i. Určitě a + b, a - b, a.b, a / b, | a |, dále
Řešení:
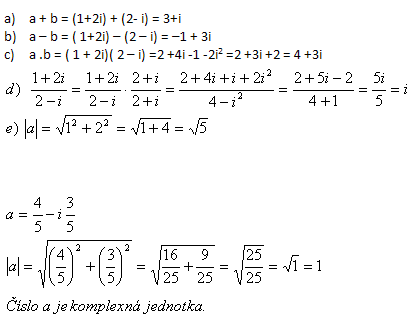
3.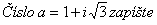
- a) v goniometrické tvaru
- b) v exponenciálním tvaru
- c) vypočítejte a5
- d) vypočítejte √ a
Řešení:
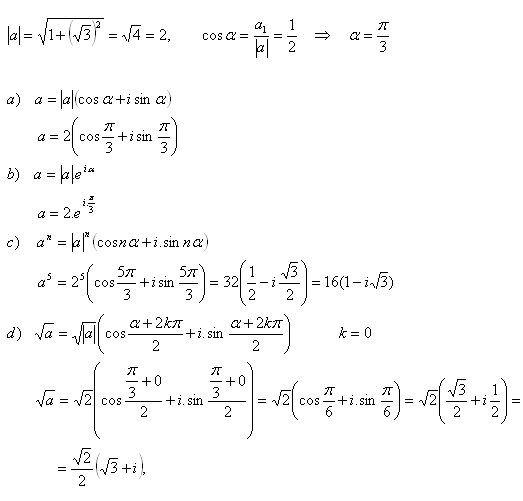
4.Vypočítejte:
Řešení:
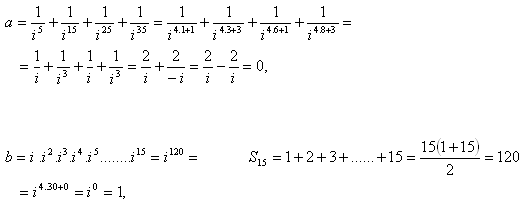
5.Vypočítejte:
Řešení:
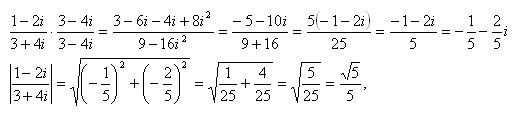
6.Najděte reálná čísla x, y tak, aby platilo:
(3 – 2i).x + (5 – 7i).y = 1 + 3i
Řešení:
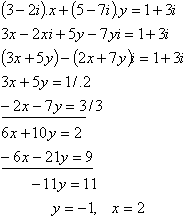
7.Vypočítejte:
Řešení:
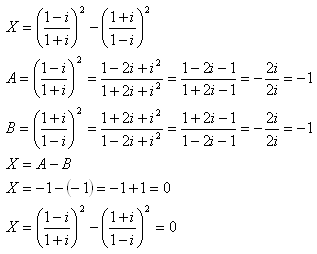
8.Čtverec má střed v počátku Gaussovy roviny, jeden vrchol je v obraze komplexního čísla a = 4 + 3i.
- a) Které komplexní čísla zobrazují zbývající vrcholy
- b) Urč obsah tohoto čtverce
Řešení:

9.Vypočítejte délku těžnice tc trojúhelníku ΔABC, jestliže jeho vrcholy A, B, C jsou obrazy komplexních čísel a = –1 –i , b = –5 + 7i , c = 9 + 8i.
Řešení:
Dĺžka ťažnice tc je dĺžka úsečky CS, kde S je stred úsečky AB
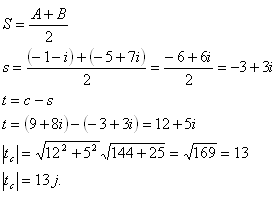
Těžnice Tc má délku 13 j.
10.Pravidelný šestiúhelník ABCDEF má střed S v počátku Gaussovy roviny a vrchol A v obraze komplexní jednotky na reálné ose. Určitě komplexní čísla, jejichž obrazy jsou v ostatních vrcholech šestiúhelníku.
Řešení:
Vrchol A : a = 1
Vrchol D : d = –1
Další vrcholy leží v jednotlivých kvadrantech Gaussovy roviny.
Trojúhelník Δ SAB je rovnostranný SA = SB = AB = 1