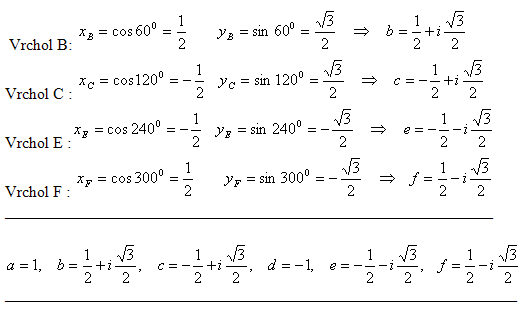Vlastnosti komplexných čísel
1. Aké vlastnosti majú komplexné čísla?
Riešenie:


2.Dané sú komplexné čísla a = 1+2i , b = 2 – i. Určite a + b, a – b, a.b, a / b, |a|, ďalej
Riešenie:
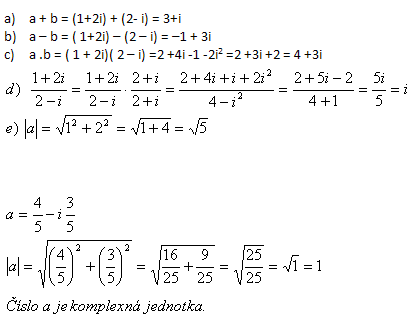
3.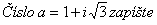
- a) v goniometrickom tvare
- b) v exponenciálnom tvare
- c) vypočítajte a5
- d) vypočítajte √a
Riešenie:
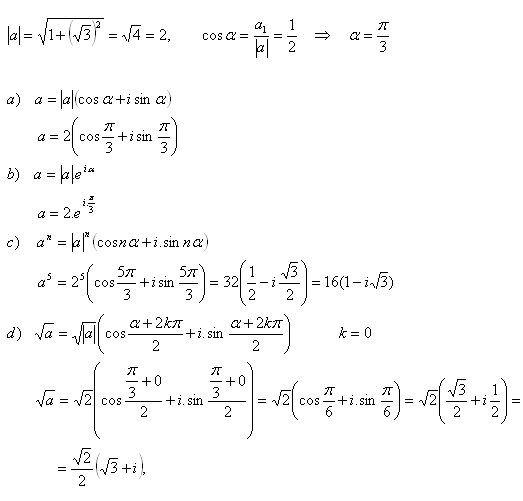
4.Vypočítajte:
Riešenie:
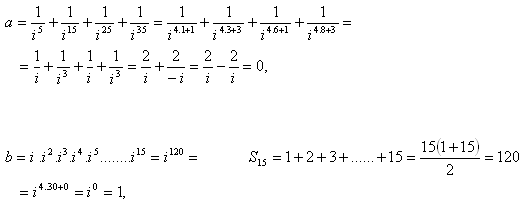
5.Vypočítajte:
Riešenie:
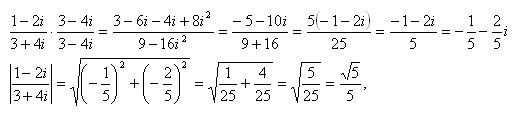
6.Nájdite reálne čísla x ,y tak, aby platilo:
(3 – 2i).x + (5 – 7i).y = 1 + 3i
Riešenie:
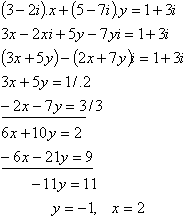
7.Vypočítajte:
Riešenie:
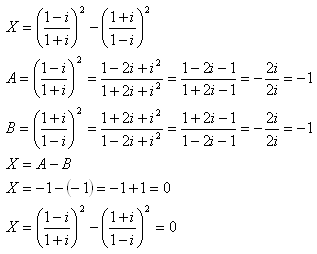
8. Štvorec má stred v počiatku Gaussovej roviny, jeden vrchol je v obraze komplexného čísla a=4 + 3i.
- a) Ktoré komplexné čísla zobrazujú zvyšné vrcholy
- b) Určite obsah tohto štvorca
Riešenie:

9.Vypočítajte dĺžku ťažnice t c trojuholníka ΔABC, ak jeho vrcholmi A,B,C sú obrazy komplexných čísiel a = –1 –i , b = –5 + 7i , c = 9 + 8i.
Riešenie:
Dĺžka ťažnice tc je dĺžka úsečky CS, kde S je stred úsečky AB
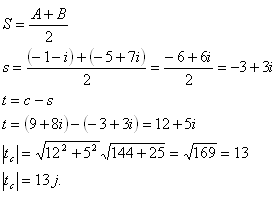
Ťažnica tc má dĺžku 13 j.
10.Pravidelný šesťuholník ABCDEF má stred S v začiatku Gaussovej roviny a vrchol A v obraze komplexnej jednotky na reálnej osi. Určite komplexné čísla , ktorých obrazy sú v ostatných vrcholoch šesťuholníka.
Riešenie:
Vrchol A : a = 1
Vrchol D : d = –1
Ďalšie vrcholy ležia v jednotlivých kvadrantoch Gaussovej roviny.
Trojuholník Δ SAB je rovnostranný SA = SB = AB = 1