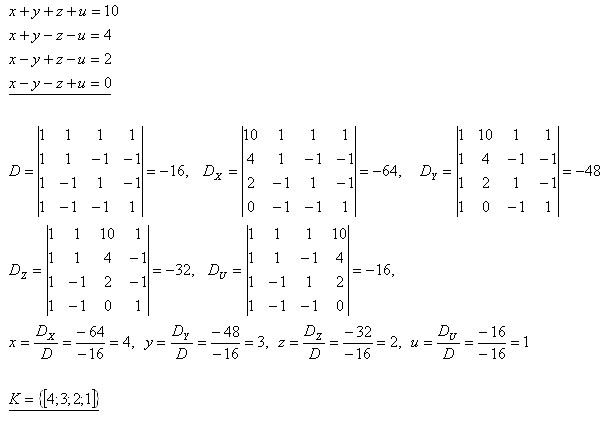Determinant
1. Čo je determinant a aké má vlastnosti?
Riešenie:
Determinant n – tého rádu je číslo D, vytvorené z n2 čísiel aik, usporiadaných do štvorcovej tabuľky z n riadkov a n stĺpcov tvaru

a11,a12,...a1n =>riadok determinatu
a11,a21,...an1 =>stĺpec determinatu
a11,a22,...ann =>hlavná diagonála
Hodnota determinantu:
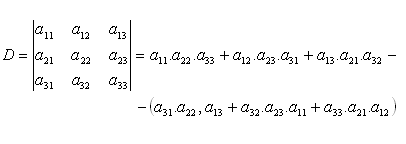
Determinant n-tého stupňa:
Determinant n-tého stupňa má n riadkov a n stípcov. (n>3) Subdeterminant (minor) Mij príslušný k prvku aij vznikne z determinantu D vynechaním i-tého riadku a j-tého stĺpca.
Algebraický doplnok (kofaktor):
Aij =(-1)i+j.aij.Mij
Rozvoj determinantu:
a.) podľa i-tého riadku:
D=ai1Mi1 + ai2Mi2 + ... + ainMin
b.) podľa j-tého stĺpca:
D=a1jM1j + a2jM2j + ... + anjMnj
2. Vyslovte vety o hodnote determinantu.
Riešenie:
- 1) Hodnota determinantu sa nezmení, ak v ňom zameníme riadky za stĺpce.
- 2) Hodnota determinantu sa nezmení, ak k ľubovoľnému riadku pripočítame (odčítame) ľubovoľný násobok ostatných riadkov.
- 3) Hodnota determinantu sa rovná nule, ak sú v niektorom riadku všetky prvky rovné nule.
- 4) Hodnota determinantu sa rovná nule, ak niektorý riadok je ľubovoľným násobkom iného riadku.
- 5) Hodnota determinantu sa rovná nule, ak má dva riadky rovnaké.
- 6) Determinant zmení znamienko, ak medzi sebou vymeníme dva riadky determinantu.
- 7) Pred determinant môžeme vybrať číslo „c“, ktorým je vynásobený niektorý riadok.
- 8) Násobiť determinant číslom „c“, znamená vynásobiť týmto číslom niektorý jeho riadok.( Len jediný riadok) c <>0
Poznámka:
Uvedené vlastnosti platia aj pre stĺpce determinantu.
3.Vyčíslite determinanty:
Riešenie:
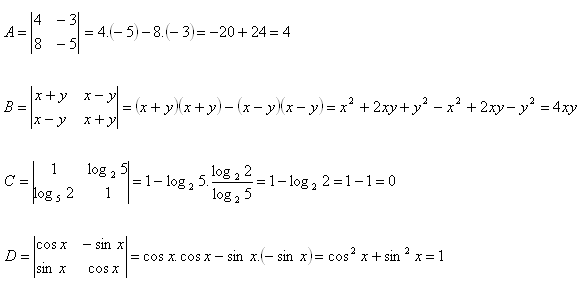
4. Vyčíslite determinanty:
Riešenie:
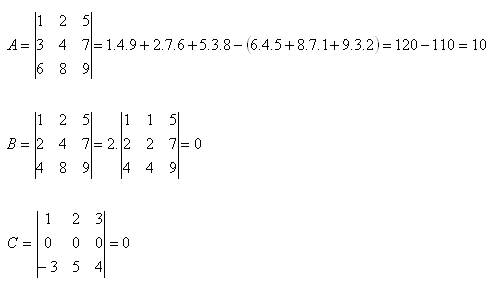
5.Vyčíslite determinanty:
Riešenie:
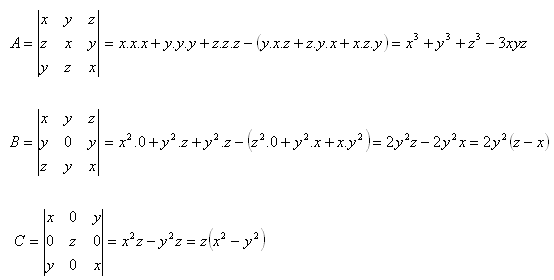
6. V množine R riešte rovnice:
Riešenie:
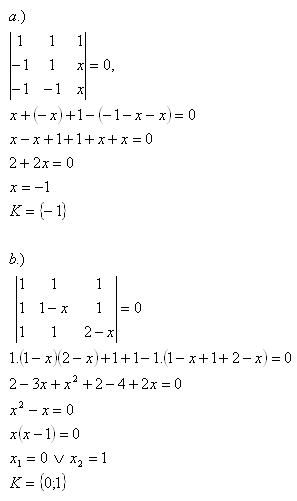
7.V množine R riešte rovnice:
Riešenie:
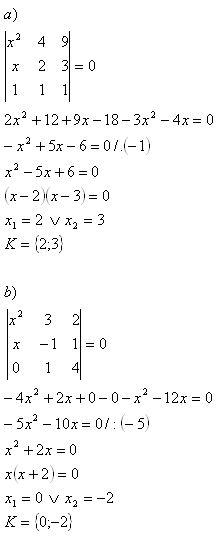
8.Vypočítajte obsah trojuholníka ABC, ktorý má vrcholy:
A[3;2], B[6;3], C[4;7]
Riešenie:
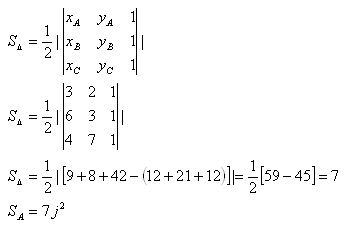
Obsah trojuholníka ABC je 7j2
9. Vypočítajte obsah trojuholníka ABC, ktorého strany majú rovnice:
Riešenie:
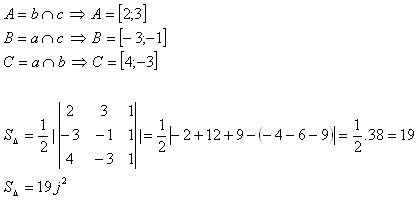
Obsah trojuholníka ABC je 19j2
10.Zistite, či body A, B, C ležia na jednej priamke, ak:
A[1;4], B[3;0], C[0;6]
Riešenie:
Podmienka aby body A[xa;ya], B[xb;yb], C[xc;yc] ležali na jednej priamke je
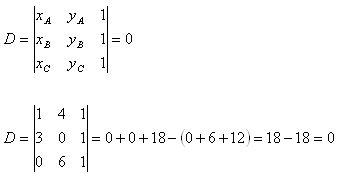
D=0 => Body A,B,C ležia na jednej priamke
11.Zistite, či body A,B,C ležia na jednej priamke, ak platí:
A[1;1], B[0;4], C[4;3]
Riešenie:
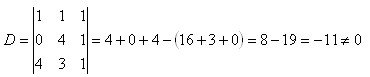
D <> 0 => Body neležia na jednej priamke
12.Dané sú body A,B,C. Zistite prvú súradnicu bodu B tak, aby body A,B,C ležali na jednej priamke. Platí:
A[0;3], B[xB;-1], C[-3;9]
Riešenie:
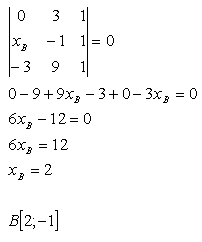
13.Napíšte rovnicu priamky, ktorá prechádza bodmi A, B ak platí:
A[3;2], B[0;4]
Riešenie:
Nech body A[xa;ya], B[xb;yb], X[x,y] ležia na priamke p, potom
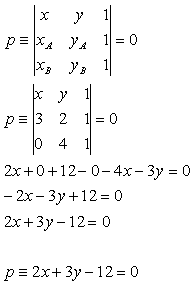
14.Napíšte rovnice strán trojuholníka ABC s vrcholmi
A[4;2], B[7;3], C[1;6]
Riešenie:
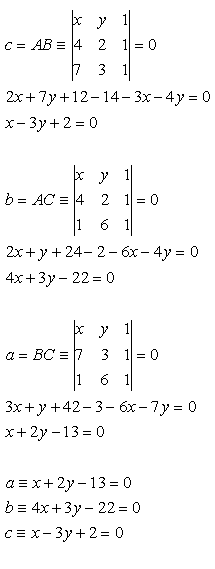
15.Vypočítajte vektorový súčin dvoch vektorov:
Riešenie:
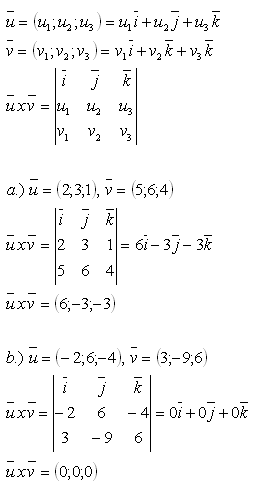
16.Riešte sústavy lineárnych rovníc:
Riešenie:
Cramerovo pravidlo 1.
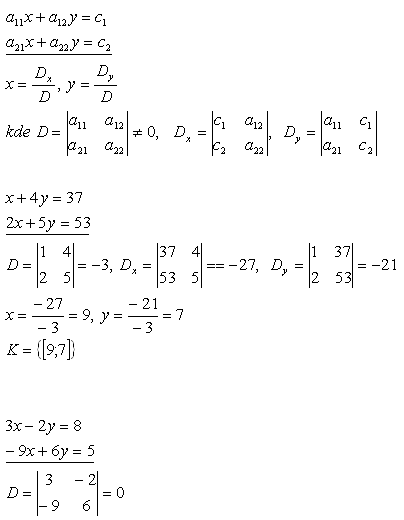
Sústava nemá riešenie
17.Riešte sústavu lineárnych rovníc:
Riešenie:
Cramerovo pravidlo 2.
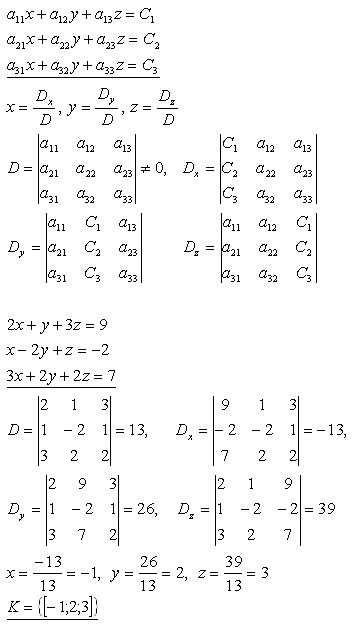
18. Riešte sústavu lineárnych rovníc:
Riešenie:
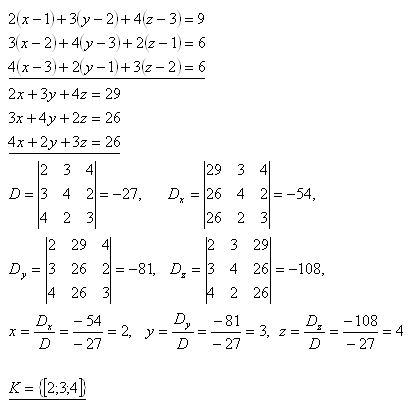
19.K danému determinantu D určite algebraický doplnok A23
Riešenie:
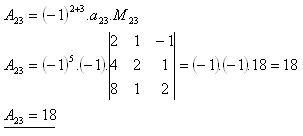
20. Vyčíslite determinant:
Riešenie:
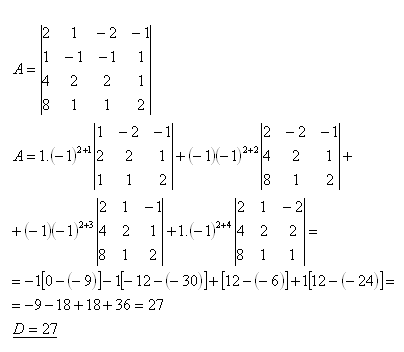
21. Vyčíslite determinant:
Riešenie:
Rozpis podľa štvrtého riadku:
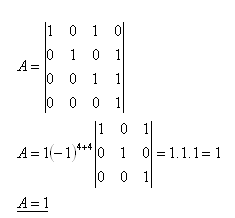
22.Zistite, či body A,B,C,D ležia v jednej rovine ak:
A[2;2;-2], B[1;1;4], C[0;2;0],D[3;1;2]
Riešenie:
Podmienka:
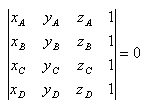
Riešenie:
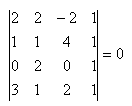
Rozpis podľa tretieho riadku:
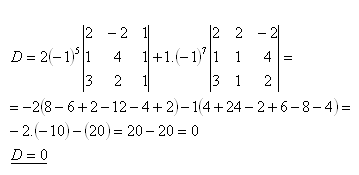
Body A,B,C,D ležia v jednej rovine.
23.Napíšte všeobecnú rovnicu roviny, ktorá je daná bodmi A,B,C ak platí
A[0;0;5], B[-2;0;1], C[1;2;4]
Riešenie:
Rovnica roviny:
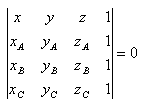
Riešenie:
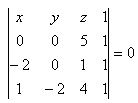
Rozpis podľa druhého riadku:
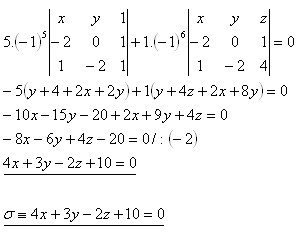
24.Napíšte všeobecnú rovnicu roviny, ktorá prechádza bodmi A,B,C, ak
A[2;1;2], B[1;-2;3], C[0;0;0]
Riešenie:
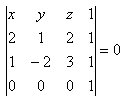
Rozpis podľa štvrtého riadku:
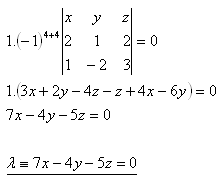
25.Riešte sústavu rovníc:
x + y + z + u = 10
x + y – z – u = 4
x – y + z – u = 2
x – y – z + u = 0
Riešenie: