Kužeľosečky
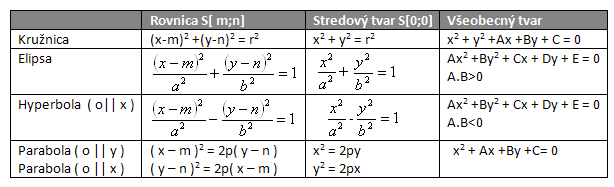
1. Čo viete o kužeľosečkách:
Riešenie:
Kružnica je množina bodov roviny, ktoré majú od pevného bodu roviny S rovnakú vzdialenosť r .S[m ; n] je stred a r polomer kružnice.
Elipsa je množina bodov roviny, ktorých súčet vzdialeností od bodov F1,F2 roviny je rovný 2a. Body F1[-e;0] , F2[e;0] sú ohniská , excentricita e2 = a2- b2, a – veľká, b – malá poloos.
Hyperbola je množina bodov roviny, pre ktoré absolútna hodnota rozdielu vzdiakeností od bodov F1,F2 roviny je rovná 2a. Body F1[-e;0] , F2[e;0] sú ohniská , excentricita e2 = a2 + b2. a – reálna ,b – imaginárna poloos. Rovnice asymtot hyperbboly: ( o || x ) : 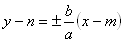
Parabola je množina bodov roviny , ktorých vzdialenosť od bodu F roviny a od priamky d ležiacej v rovine je rovnaká. Bod F je ohnisko paraboly, d – riadiaca priamka . Bod F neleží na d. Hodnota p je parameter paraboly.
Vzájomnú polohu kužeľosečky a priamky zistíme riešením sústavy ich rovníc, čo vedie na riešenie kvadratickej rovnice. Ak D>0 priamka je sečnica, ak D = 0 priamka je dotyčnica, ak D<0 priamka je nesečnica.
2.Napíšte rovnicu kružnice, ktorá má polomer r = 8 a dotýka sa obidvoch súradnicových osí.
Riešenie:
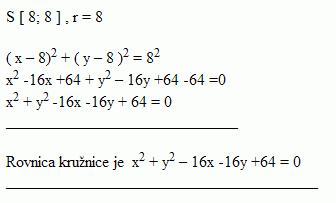
3.Napíšte rovnicu kružnice, ktorej priemerom je úsečka AB, ak A [-1 ; 4 ], B [ 5 ; 6 ]
Riešenie:
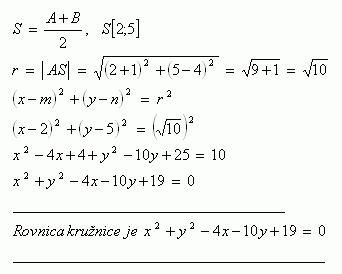
4. Dokážte, že rovnice k x2 + y2 +2x +4y +1 = 0 a k2 : x2 +y2-8x +6y + 9 = 0 predstavujú kružnice. Napíšte rovnicu priamky, ktorá prechádza stredmi týchto kružníc.
Riešenie:
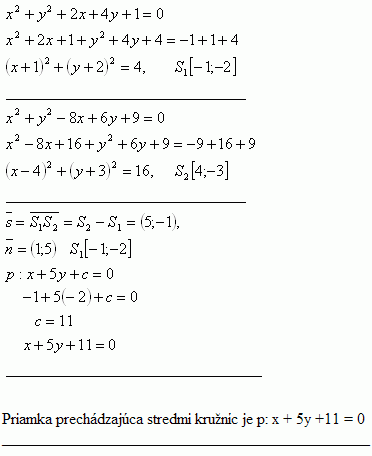
5.Bodom A [4; 2 ] prechádza kružnica, ktorá sa dotýka súradnicových osí. Napíšte rovnicu tejto kružnice.
Riešenie:
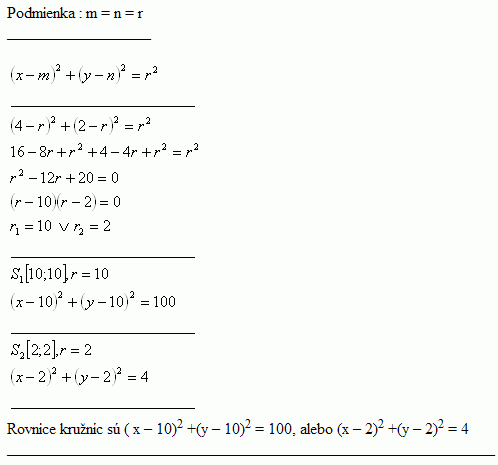
6. Bod A [-4 ; 5] je vrcholom štvorca, ktorého uhlopriečka leží na priamke p : [ 7x – y + 8 = 0 ]. Napíšte rovnicu kružnice, ktorá je štvorcu opísaná.
Riešenie:
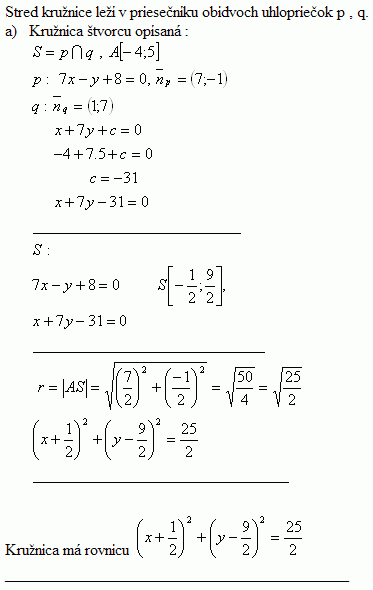
7.Napíšte rovnicu kružnice, ktorej stred S leží na priamke p :[ x – y – 1 = 0 ] a ktorá zároveň prechádza bodmi A [ -1; -1 ] a B [ 0; 6 ]
Riešenie:
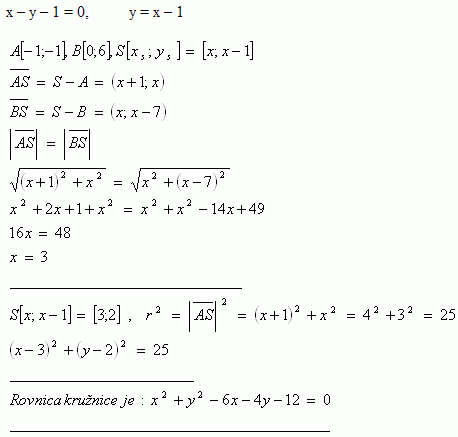
8.Napíšte rovnicu kružnice, ktorá prechádza bodmi K [2;-1] L [5;-2] M [10;3]
Riešenie:
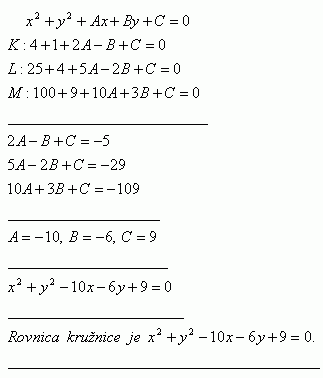
9.Vyšetrite vzájomnú polohu priamky p: [2x – y – 6 = 0] a kružnice k: [x2 + y2 – 4x -5y -1 = 0]
Riešenie:

10. Napíšte rovnicu kružnice súmernej s kružnicou k1: ( x – 1 )2 +( y – 2 )2 = 1 vzhľadom na priamku p: x – y – 3 = 0
Riešenie:
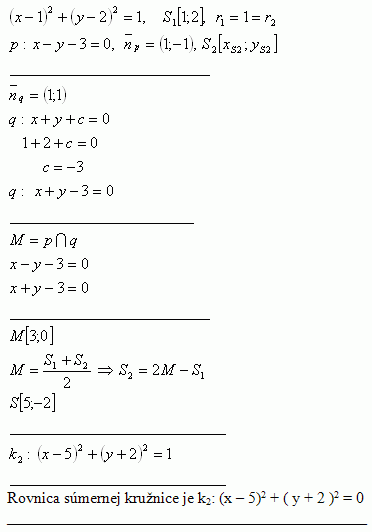
11.Dva vrcholy kosoštvorca sú v ohniskách elipsy 9x2 + 25y2 - 225 = 0, ďalšie dva sú vo vrcholoch elipsy na jej vedľajšej osi. Vypočítajte obsah kosoštvorca.
Riešenie:
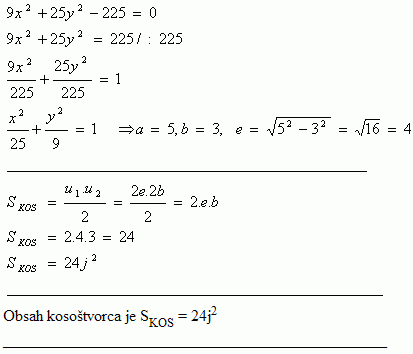
12.Určite rovnicu elipsy v stredovom tvare S [0;0] , ktorá prechádza bodmi A [8;3] a [6;4]
Riešenie:
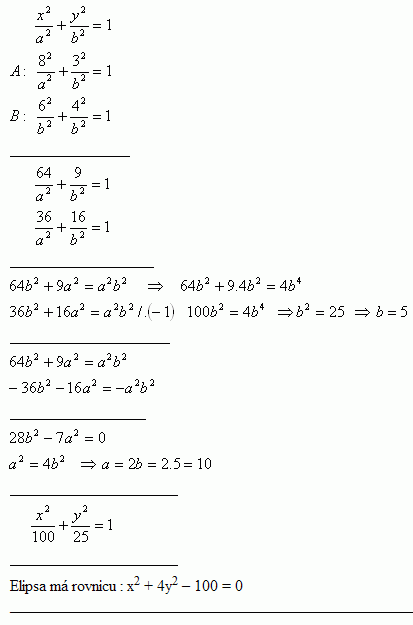
13.Napíšte rovnicu priamky, ktorá prechádza bodom A [1;5] a stredom elipsy 4x2 + 9y2 - 24x + 36y +36 = 0
Riešenie:
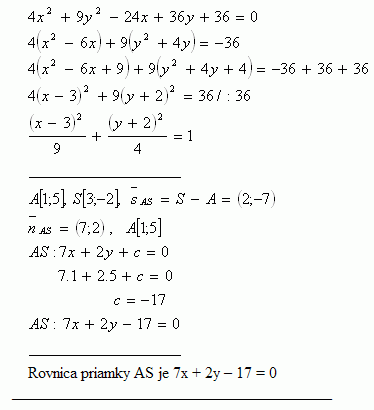
14.Do elipsy 2x2 + y2 – 4x + 4y – 108 = 0 je vpísaný štvorec ABCD. Zistite aký je jeho obvod a obsah.
Riešenie:
2x2 + y2 – 4x + 4y – 108 = 0
(2x2-4x) + (y2+4y) = 108
2(x2-2x+1) +(y2+4y+4) = 108+2+4
2(x-1)2 + ( y+2)2 =114 y = x
2(x2- 2x+1 ) + ( x2 +4x +4 ) = 114
3x2 – 108 = 0
3x2 = 108
x2 = 36
x =+- 6
X = (1+x ; -2+x )
A [7; 4 ] B [-5; 4] C [ -5; -8] D [ 7 ; -8]
a = | AB| = |BC| = |CD| = |DA| = 12
a = 12 j
O = 4a , S = a2
O = 4.12 S = 122
O = 48 j S = 144 j2
Obvod štvorca je O = 48 j, jeho obsah je S = 144 j2
15. Zistite vzdialenosť stredu elipsy 4x2 + 9y2 -16x + 36y + 16 = 0 od priamky 5x-12y+5 = 0
Riešenie:
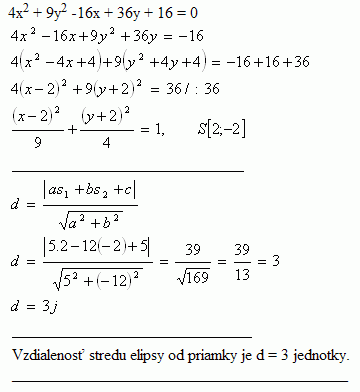
16.Na elipse so stredom S [ 3; 2 ], osou b = 4, excentricitou e = 3 nájdite bod, ktorého súradnica y = 2
Riešenie:
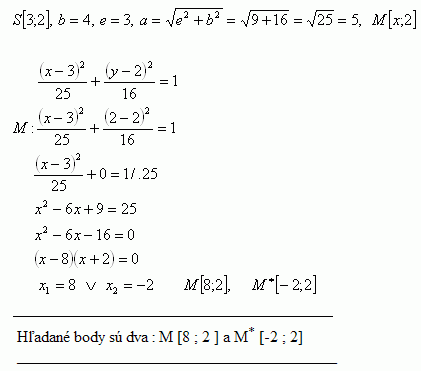
17.Daný je trojuholník Δ ABC so stranami |AB| = 6, |AC| = 7, |BC| = 3. Napíšte rovnicu elipsy, ktorá má ohniská v jeho dvoch vrcholoch a prechádza tretím vrcholom trojuholníka.
Riešenie:

18.Určite a vyšetrite kužeľosečku, ktorá prechádza bodmi : K[0;0], L[8;0], M[0;6], N[8;6]. O[2;-2]
Riešenie:
Ax2 + By2 +Cx + Dy + E = 0
Riešte sústavu rovníc:
K: 0 + 0 + 0 + E = 0
L: 64A + 0 + 8C + 0 +E = 0
M: 0 + 36B + 0 + 6D + E = 0
N: 64A + 36B + 8C + 6D + E = 0
O: 4A + 4B + 2C – 2D + E = 0
A = 4, B = 3, C = -32, D = -18, E = 0
4x2 + 3y2 – 32x -18y = 0 .
Kužeľosečka je elipsa s rovnicou 4x2 + 3y2 -32x -18y = 0
19.Vypočítajte dĺžku tetivy, ktorú priamka 2x + y – 14 =0 vytína na elipse 4x2 +y2 -100= 0
Riešenie:
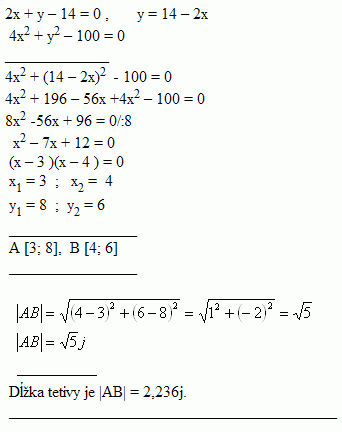
20.Napíšte rovnicu elipsy , keď je daný bod M [3;-1], ktorý je koncovým bodom malej poloosi b, ohniská ležia na priamke p: y + 6 = 0. Pre excentricitu elipsy platí:
Riešenie:
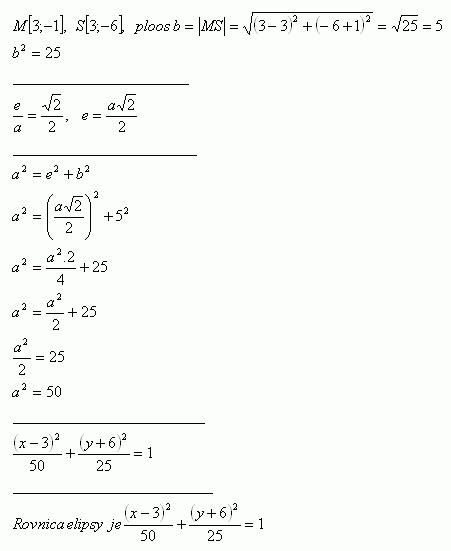
21.Určite stred a poloosi hyperboly 9x2 -16y2 -36x + 32y – 124 = 0. Určite tiež rovnice asymptot hyperboly.
Riešenie:
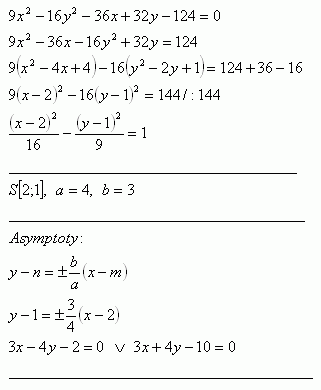
22. Napíšte rovnicu hyperboly, ak pre jej ohniská platí: F1 [-10;2], F2 [16;2]. Reálna os 2a = 24
Riešenie:
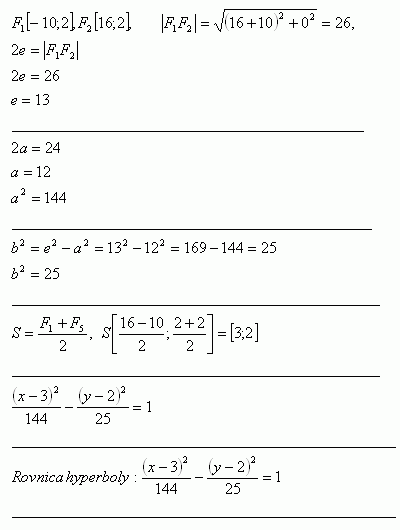
23. Napíšte rovnicu priamky na ktorej leží os súmernosti úsečky, ktorá spája stredy hyperbol x2 – y2 +6x -8y – 107 = 0, a 16x2 -9y2 -160x + 36y +220 = 0
Riešenie:
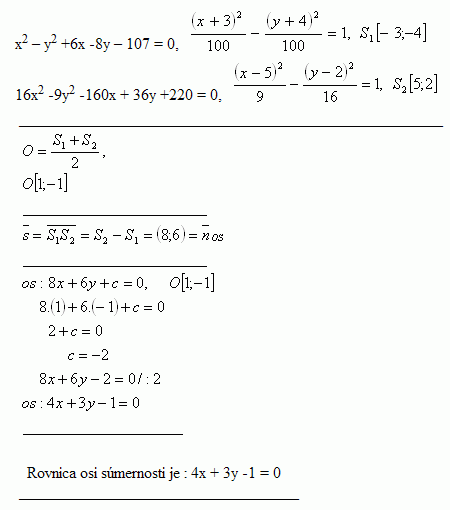
24.Daná je hyperbola 16x2 – 25y2 – 400 = 0. Napíšte: a) rovnice asymptot, b) uhol asymptot
Riešenie:
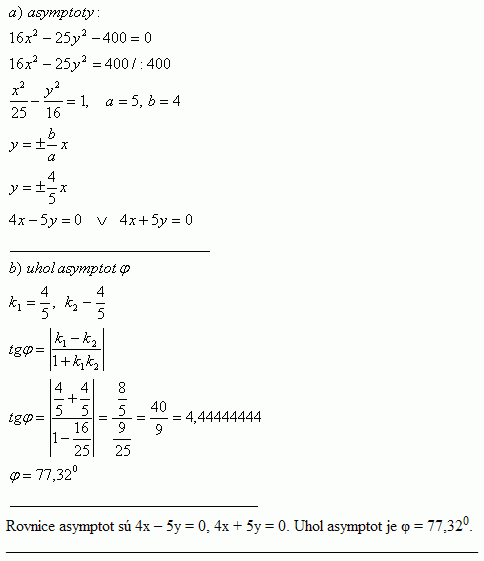
25.Napíšte osovú rovnicu hyperboly, ktorá prechádza bodmi:
Riešenie:
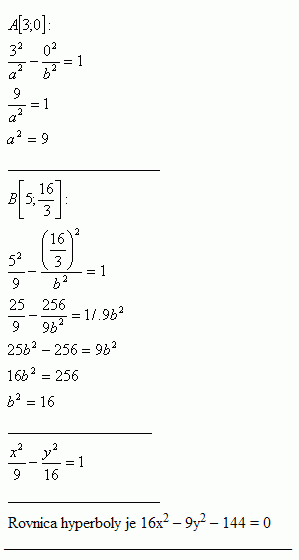
26.Dokážte, že súčin vzdialeností ľubovoľného bodu M hyperboly 2x2 – y2 – 2 = 0 od jej asymptot je stály a rovný 2 : 3
Riešenie:

27.Nájdite množinu všetkých bodov v rovine, ktoré majú od bodu M [-5;0 ] a od priamky p: 5x + 16 = 0 konštantný pomer vzdialeností rovný 5 : 4
Riešenie:
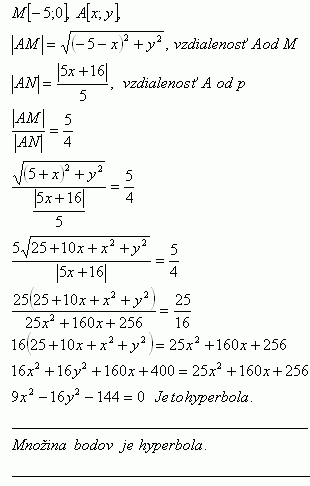
28. Napíšte rovnicu hyperboly, ktorej vrcholy sú v ohniskách elipsy x2 + 2y2 – 18 = 0 a ktorej ohniská sú vo vrcholoch tejto elipsy
Riešenie:
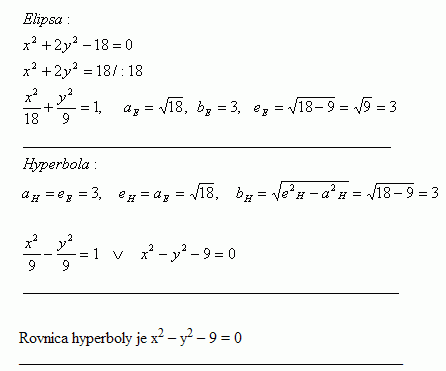
29. Napíšte rovnicu priamky, ktorá prechádza bodom M [5 ; 4] a vrcholom V paraboly y2- 6x +10y +31 = 0
Riešenie:
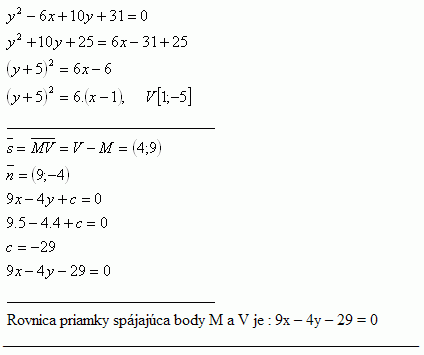
30. Dané sú paraboly x2 - 8x - 3y +10 = 0 a x2 + 14x - 4y +61 = 0. Vypočítajte vzdialenosť ich vrcholov |V1V2|
Riešenie:
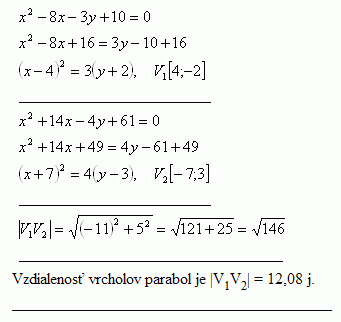
31.Napíšte rovnicu paraboly (o||y) ktorá prechádza bodmi K[1;2], L[3;1], M[7;5].
Riešenie:
x2 +Ax + By + C = 0
K: 1 + A + 2B +C = 0
L: 9 +3A + B +C = 0
M: 49 +7A +5B +C = 0
A = -6, B = -4, C = 13,
x2 – 6x – 4y +13 = 0
x2 – 6x – 4y +13 = 0
x2 – 6x +9 = 4y -13 +9
(x – 3)2 = 4y – 4
(x – 3)2 = 4.(x –1)
Rovnica paraboly je (x – 3)2 = (y – 1) .
32.Na akej čiare ležia body v rovine, ktorých súčet vzdialeností od osi x a od bodu B[8;0] je stále rovnaký a rovný 24.
Riešenie:
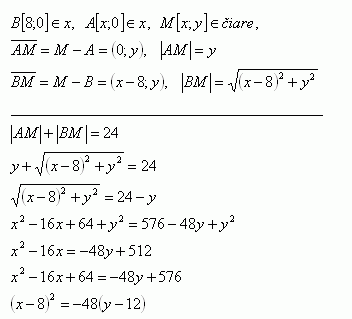
Čiara je parabola (x-8)2 = -48(y-12), o||-y
33.Parabola má rovnicu p: y2 = 8x. Vypočítajte súradnice štvorca ABCD, ak A splýva s vrcholom paraboly, C leží na osi x a body B,D ležia na parabole.
Riešenie:
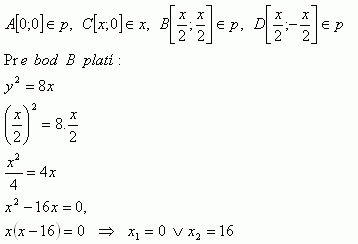
Vrcholy štvorca sú: A[0;0], B[8;8], C[16;0], D[8;-8]
34.Určite stranu rovnostranného trojuholníka Δ ABC vpísaného do paraboly y2 = 5x
Riešenie:
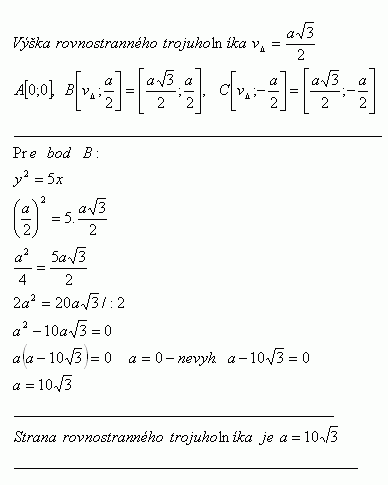
35. Vypočítajte dĺžku tetivy, ktorú vytína parabola y2 = 2x na elipse 4x2 + 9y2 – 400 = 0.
Riešenie:
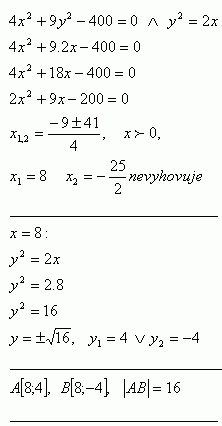
Dĺžka tetivy je |AB|=16j.
36.Určite polohu bodov A.B,C,D v ktorých elipsa x2 + 2y2 -18 = 0 pretína hyperbolu x2 – y2 – 9 = 0.
Riešenie:
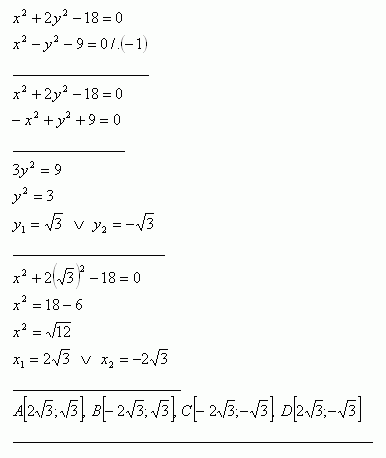
37. Na elipse nájdite body, ktoré majú od pravého ohniska (e>0) vzdialenosť r=14. Rovnica elipsy:
Riešenie:
Elipsa : a2 = 100, b2 =36, e2 = a2 – b2 = 100 – 36 = 64, e = 8
Kružnica : S = F2[8;0] r = 14
( x – 8 )2 + y2 = 142
x2 – 16x + 64 +y2 – 196 = 0 y2 = -x2 +16x + 132
Elipsa :
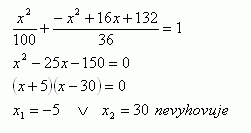
Hľadané body:
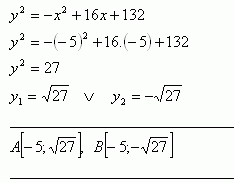
38.Vypočítajte obvod obdĺžnika ABCD, ktorého vrcholy sú priesečníky kružnice k: x2 + y2 = 50 a hyperboly h: x2 – y2 = 48.
Riešenie:
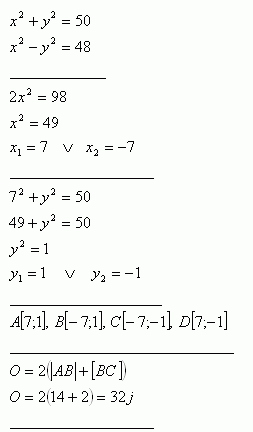
Obvod obdĺžnika je O = 32j