Slovné úlohy
1. Trojuholník má obvod 35 cm. Jedna jeho strana je štyrikrát väčšia ako druhá a o 1 cm väčšia ako tretia. Určite veľkosti strán trojuholníka.
Riešenie:
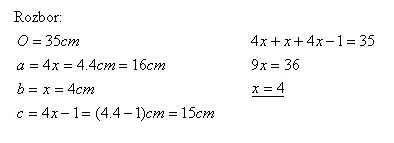
Veľkosti strán trojuholníka sú: a = 16 cm, b = 4 cm a c = 15 cm
2. V triede je 30 žiakov. Z matematiky nebola na vysvedčení horšia známka ako dvojka. Určite počet žiakov, ktorí mali jednotku z matematiky, ak trieda mala priemer z matematiky 1,4.
Riešenie:
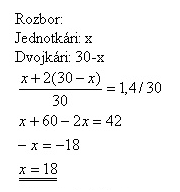
V triede je 18 jednotkárov a 12 dvojkárov.
3. Koľko chlapcov súťažilo, ak štvrtina súťažiacich bola v cieli pred Jankom a dve tretiny za ním?
Riešenie:
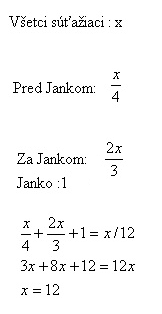
Všetkých súťažiacich bolo 12.
4. Do triedy chodí 30 chlapcov a istý počet dievčat. Lyžiarskeho výcviku sa zúčastnilo 28 chlapcov a všetky dievčatá, čo bolo 95% všetkých žiakov. Koľko % žiakov triedy tvoria dievčatá?
Riešenie:
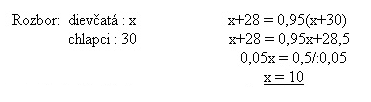
V triede je 10 dievčat, čo je 25% zo 40 žiakov.
5. 120 litrov vína stočili do 141 fliaš, niektoré boli litrové, iné 0,7 litrové. Koľko bolo ktorých?
Riešenie:
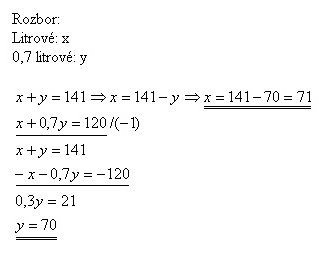
Litrových fliaš bolo 71, 0,7 litrových bolo 70.
6. Murár postaví múr za 30 hodín. Dvaja učni by ten istý múr postavili každý za 40 hodín. Za koľko hodín postavia múr spoločne?
Riešenie:
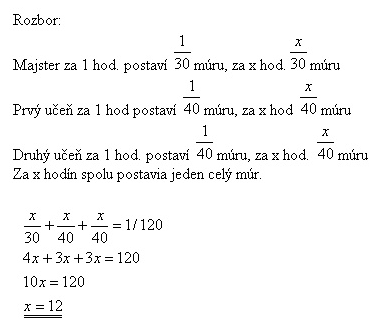
Spoločne postavia múr za 12 hodín.
7. Obvod obdĺžnika má 82 m, dĺžka jeho uhlopriečky je 29 m. Určite rozmery obdĺžnika.
Riešenie:
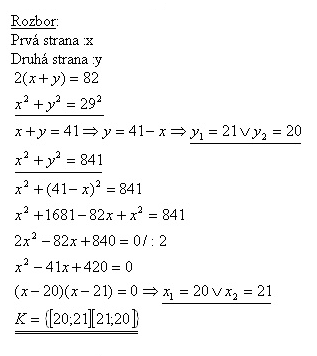
Rozmery obdĺžnika sú 20 m a 21 m.
8. Obvod pravouhlého trojuholníka má 84 cm, prepona 37 cm. Vypočítajte dĺžky odvesien.
Riešenie:
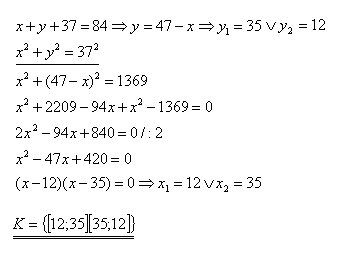
Odvesny trojuholníka sú 12 cm a 35 cm.
9. Dva rezistory zapojené sériovo dávajú výsledný odpor 18 Ω, paralelne 4 Ω. Určite odpory jednotlivých rezistorov.
Riešenie:
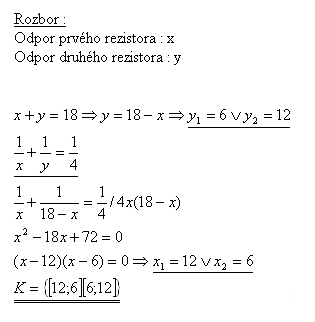
Odpory rezistorov sú 12 Ω a 6 Ω.
10. Vypočítajte strany pravouhlého trojuholníka ak viete, že má obsah S = 180 m2 a jedna jeho odvesna je o 31 m dlhšia ako druhá.
Riešenie:
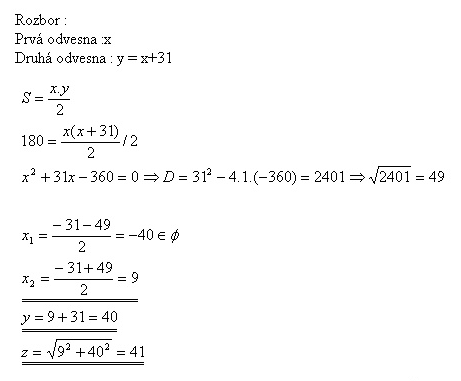
Odvesny pravouhlého trojuholníka sú 9 m, 40 m a prepona 41 m.
11. Výslednica dvoch síl, ktoré zvierajú pravý uhol má veľkosť 25 N. Ak menšiu silu zväčšíme o 8 N a väčšiu zmenšíme o 4 N, výslednica síl sa nezmení. Vypočítajte obidve sily.
Riešenie:
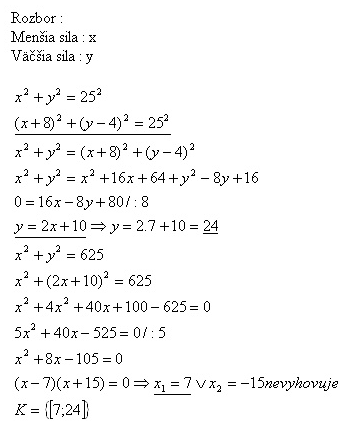
Hľadané sily sú 7 N a 24 N.
12. Ktorý x-uholník má 54 uhlopriečok?
Riešenie:
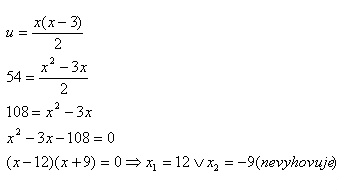
54 uhlopriečok má 12-uholník.
13. Na obdĺžnikovej ploche s rozmermi 12 m a 10 m chceme mať taký obdĺžnikový kvetinový záhon s rozlohou 8 m2, aby jeho okraje boli rovnako vzdialené od okrajov plochy. Vypočítajte rozmery záhona.
Riešenie:

Rozmery záhona sú 4 m a 2 m.
14. Dva mnohouholníky majú spolu 24 strán a 109 uhlopriečok. Koľko strán má každý z nich?
Riešenie:
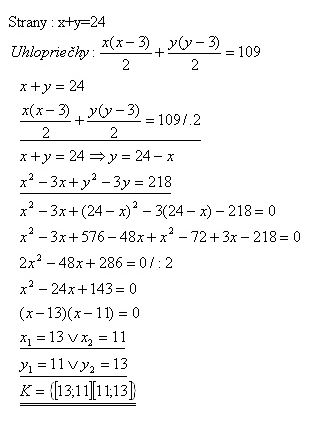
Mnohouholníky majú 13 a 11 strán.
15. V pravouhlom trojuholníku je dĺžka prepony 65 m a rozdiel odvesien 23 m. Vypočítajte obvod tohto trojuholníka.
Riešenie:
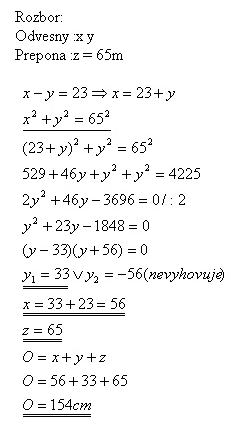
Obvod trojuholníka je 154 cm.
16. Vzdialenosť stredov dvoch kružníc dotýkajúcich sa zvonka je 12 cm. Súčet obsahov obidvoch príslušných kruhov je 80pí cm2. Určite polomery kruhov.
Riešenie:
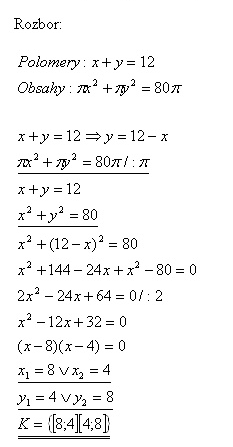
Polomery kruhov sú 8 cm a 4 cm.
17. Na schodišti vysokom 3,6 m sa zväčšil počet schodov o 3, preto výška schodu sa zmenšila o 4 cm (0,04 m). Koľko schodov má schodište?
Riešenie:
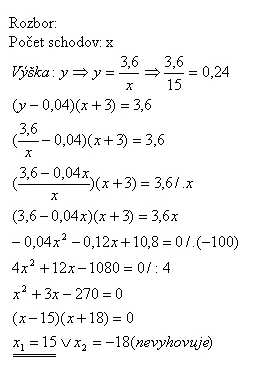
Schodov je 15, každý má výšku 0,24 m.
18. Ak vynásobíme dvojciferné číslo súčtom jeho číslic, dostaneme súčin 1666. Počet desiatok daného čísla je o 1 väčší než počet jednotiek. Ktoré je to číslo?
Riešenie:
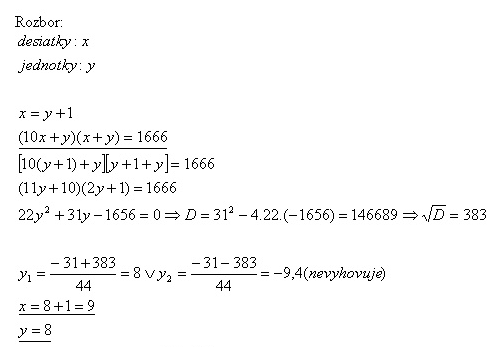
Jedná sa o číslo 98.
19. Povrchy dvoch kociek, z ktorých jedna má hranu o 22 cm dlhšiu ako druhá, sa líšia o 19272 cm2. Určite dĺžky hrán obidvoch kociek.
Riešenie:
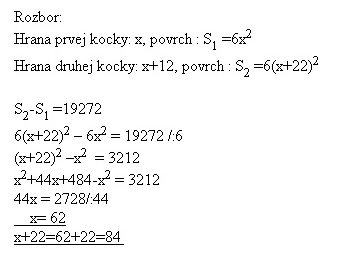
Hrany kociek sú 62 cm a 84 cm.
20. Hrana druhej kocky je o 2 cm dlhšia ako hrana prvej kocky. Rozdiel objemov kociek je 728 cm3. Vypočítajte veľkosti hrán obidvoch kociek.
Riešenie:
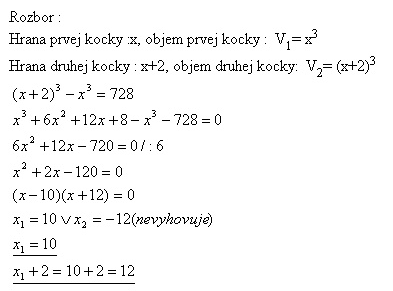
Hrana prvej kocky je 10 cm, druhej 12 cm.
21. Vo vodojeme, ktorý má tvar kvádra je 1500 hl (150 m3) vody, výška vody je 2,5 m. Určite rozmery dna, ak jeden rozmer je o 4 m väčší ako druhý.
Riešenie:
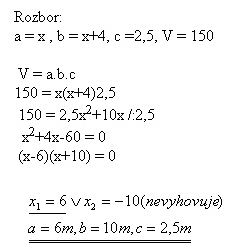
Rozmery dna sú 6 m a 10 m.
22. Vypočítajte objem valca, ktorého polomer je o 2 cm kratší ako výška a povrch má 704 cm2.
Riešenie:
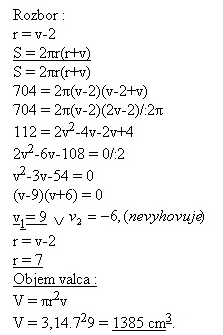
Objem valca je 1385 cm3.
23. Obvod kosoštvorca je 104 cm, obsah 480 cm2. Určite dĺžky uhlopriečok.
Riešenie:
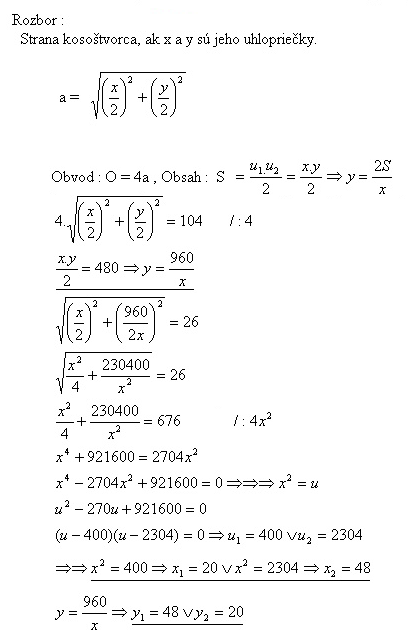
Uhlopriečky kosoštvorca majú veľkosť 20 cm a 48 cm.
Videoprezentácie sú zdieľané z portálu NAUČ SA MATIKU.