Matice
1. Aké sú základné vlastnosti matíc.
Riešenie:
Obdĺžniková schéma m, n reálnych čísiel usporiadaných do m riadkov a n stĺpcov sa nazýva matica (typu m,n) .Ak m = n je to štvorcová matica n – tého stupňa. Čísla a11 , a32, ... amn sa nazývajú prvky matice.
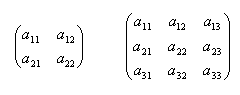
Nulová matica: Jednotková matica:
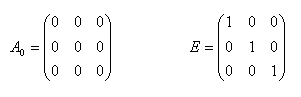
Inverzná matica A–1:
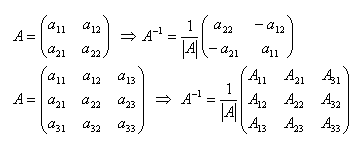
Súčet matíc A + B
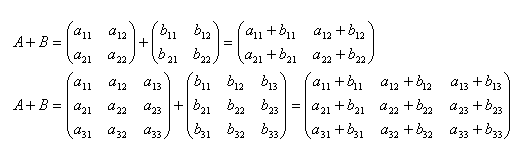
2. Vysvetlite postup pri násobení dvoch matíc.
Riešenie:
Súčin dvoch matíc má len vtedy zmysel, keď ľavá matica má toľko stĺpcov, ako má pravá matica riadkov. Takéto matice sa nazývajú „komformabilné“.
Súčin matíc nie je komutatívny!
Násobenie matice číslom :
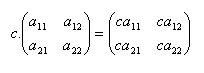
Súčin matíc A.B
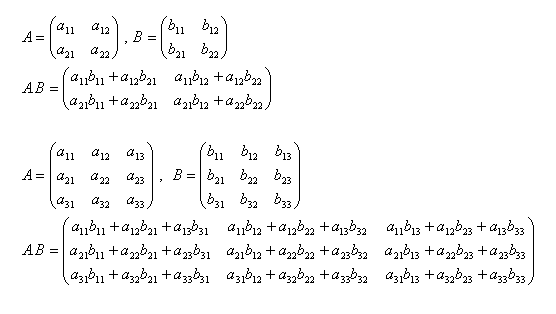
3.Spočítajte matice A+B a M+N ak platí
Riešenie:
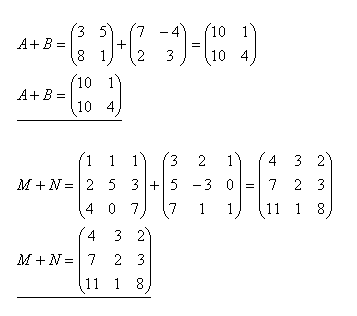
4.Vynásobte matice A.B a C.D ak platí :
Riešenie:
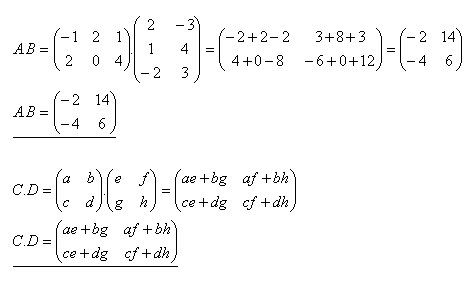
5.Ukážte, že súčin matíc nie je komutatívny.
Riešenie:
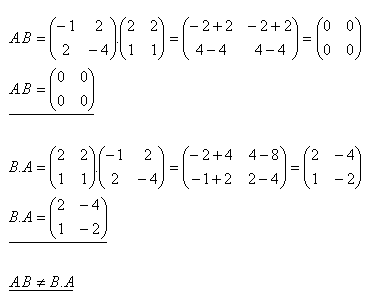
6.Daná je matica A. Zistite maticu A2 ak platí :
Riešenie:
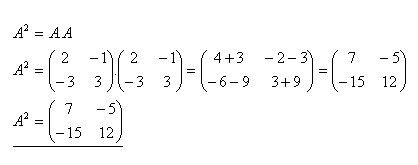
7.Daná je matica B. Zistite maticu B2 ak platí :
Riešenie:
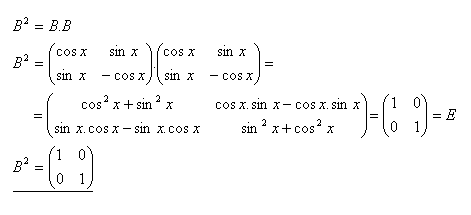
8.Zistite súčin matíc A.B ak platí:
Riešenie:
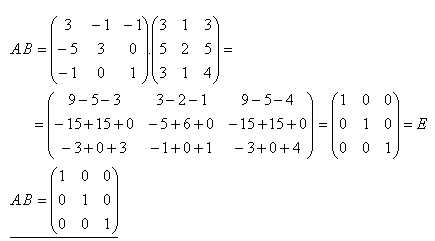
9.Vysvetlite postup pri výpočte inverznej matice A–1 z matice A.
Riešenie:
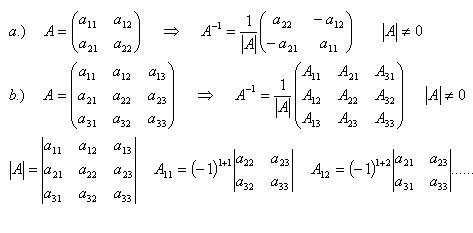
Pri skúške musí byť inverzná matica v súčine zľava.
Pre súčin matíc neplatí komutatívny zákon.
10.K matici A zistite inverznú maticu A–1 a urobte skúšku ak platí :
Riešenie:
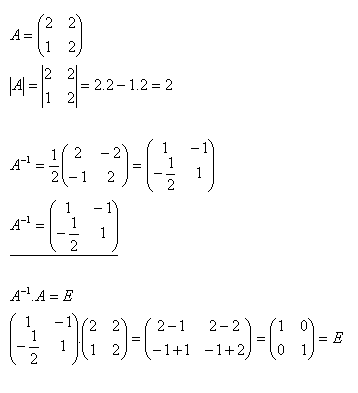
11.K matici A zistite inverznú maticu A–1 a urobte skúšku ak platí
Riešenie:
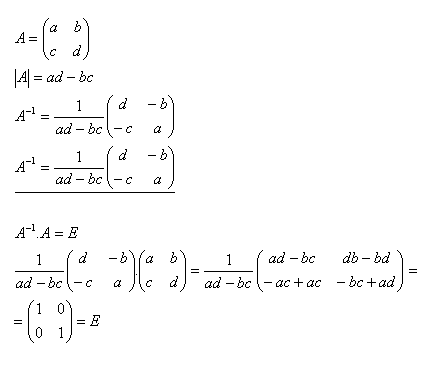
12.Vypočítajte inverznú maticu A–1 k matici A, ak platí
Riešenie:
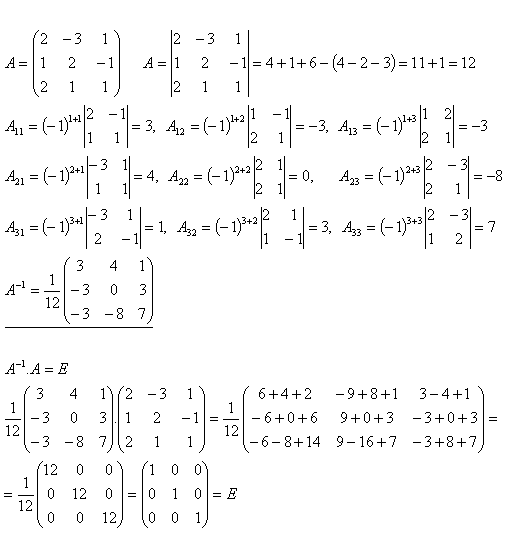
13.Vypočítajte inverznú maticu A–1 k matici A a urobte skúšku (Pozrite príklad 12), ak platí
Riešenie:
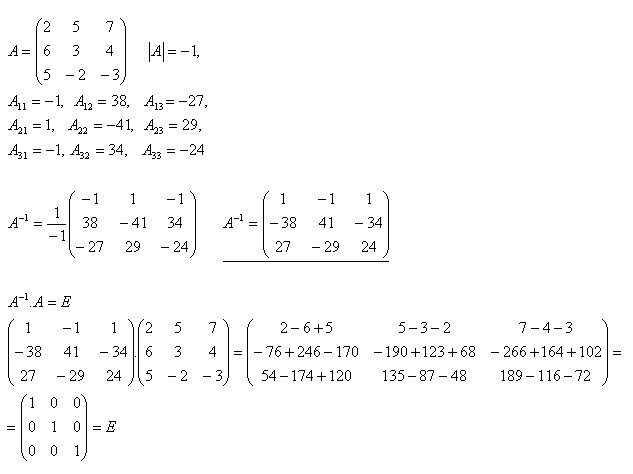
14.Riešte maticovú rovnicu A + X = B ak platí :
Riešenie:
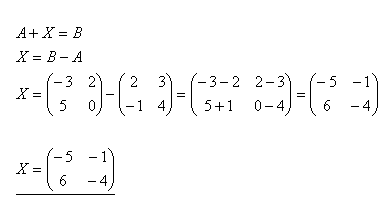
15.Vypočítajte maticu X z rovnice 2A + 3X = B ak platí :
Riešenie:
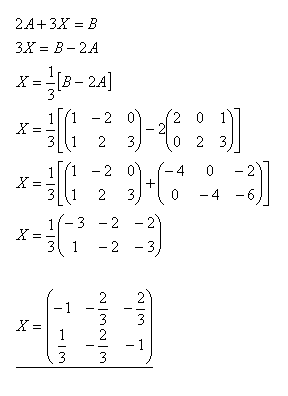
16.Riešte maticovú rovnicu A.X = B a urobte skúšku ak platí :
Riešenie:
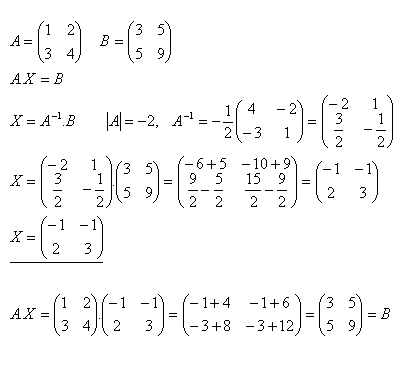
17.Riešte rovnicu A.X = B a urobte skúšku ak platí :
Riešenie:
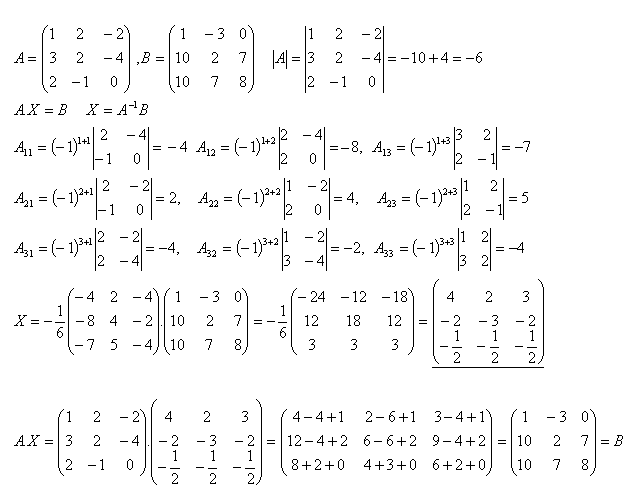
18.Vysvetlite postup pri riešení sústavy lineárnych rovníc pomocou inverznej matice.
Riešenie:
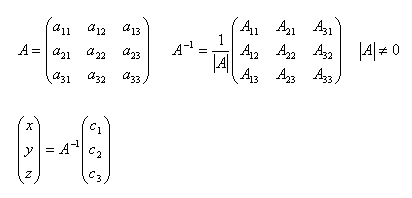
19.Pomocou inverznej matice riešte sústavu rovníc:
Riešenie:
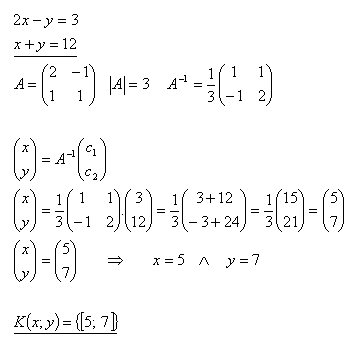
20.Pomocou inverznej matice riešte sústavu rovníc:
Riešenie:
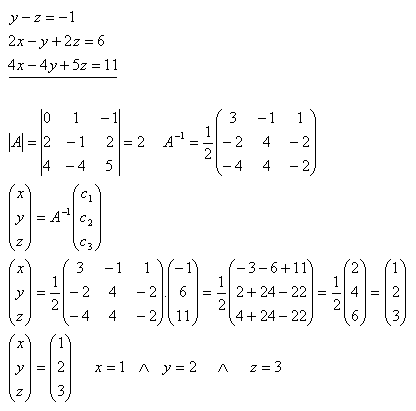
21.Pomocou inverznej matice riešte sústavu rovníc:
Riešenie:
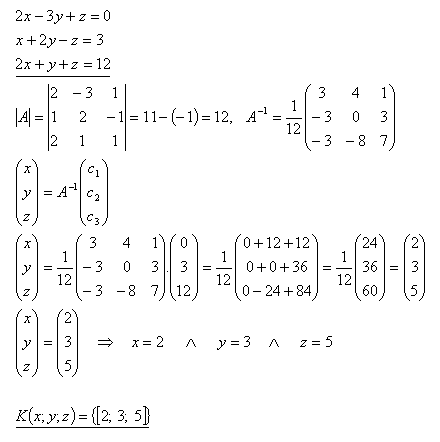
22.Pomocou inverznej matice riešte sústavu rovníc:
Riešenie:
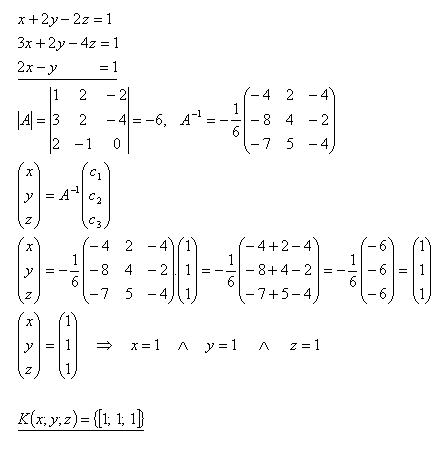
23.Vysvetlite pojem „hodnosť matice“ a podmienky riešenia sústavy lineárnych rovníc Gaussovou metódou.
Riešenie:
Hodnosť matice h je číslo, ktoré udáva maximálny počet lineárne nezávislých riadkov matice. Hodnosť matice sa nezmení ak:
- a.) zameníme poradie jej riadkov
- b.) ľubovoľný riadok vynásobíme číslom rôznym od nuly
- c.) k ľubovoľnému riadku pripočítame iný riadok
- d.) k ľubovoľnému riadku pripočítame lineárnu kombináciu iných riadkov
- e.) vynecháme riadok, ktorý je lineárnou kombináciou iných riadkov
- f.) vynecháme nulový riadok
- g.) vymeníme riadky za stĺpce ( vznikne „transponovaná matica“)
Uvedené vlastnosti hodnosti matice platia aj pre stĺpce.
Frobeniova veta:
Sústava lineárnych rovníc má len vtedy riešenie, ak hodnosť matice sústavy h sa rovná hodnosti jej rozšírenej matici h/.
h = h/
a.) h = h/ a h = n jediné riešenie
b.) h = h/ a h<n nekonečne veľa riešení (n je počet neznámych v sústave)
24.Gaussovou metódou riešte sústavu rovníc:
Riešenie:
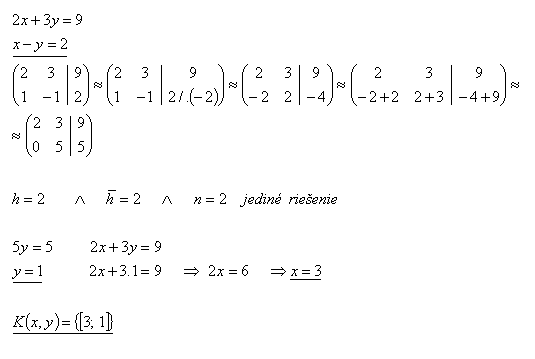
25.Riešte sústavu rovníc Gaussovou metódou:
Riešenie:
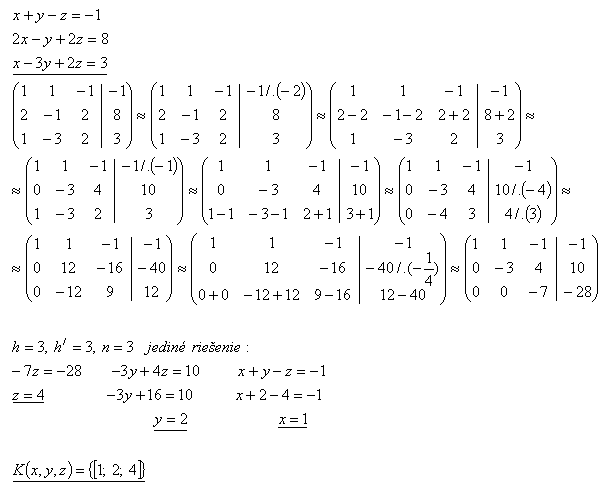
26.Riešte sústavu lineárnych rovníc Gaussovou metódou:
x + 2y + 3z =0
2x – y + z = 3
3x + y – z = 5
Riešenie:
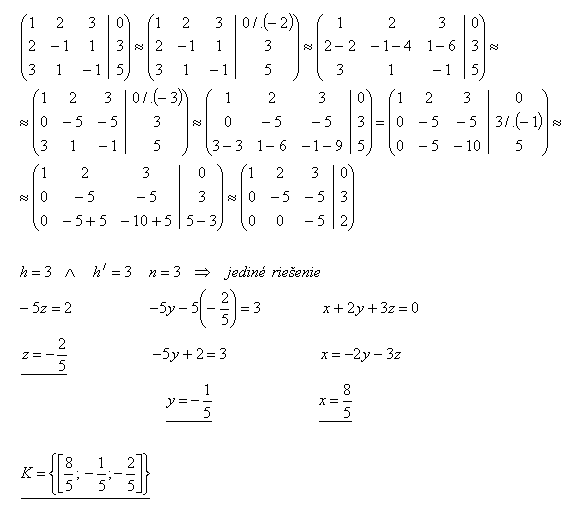
27.Riešte sústavu rovníc Gaussovou metódou:
Riešenie:

Videoprezentácie sú zdieľané z portálu NAUČ SA MATIKU.
⁞