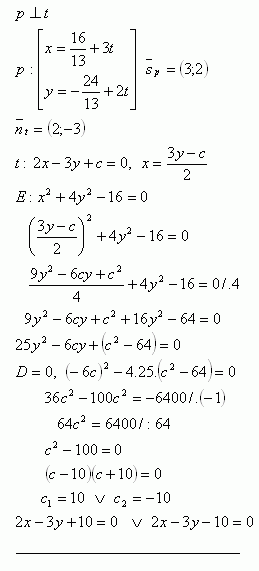Priamka a kužeľosečka
1. Čo viete o vzájomnej polohe priamky a kužeľosečky
Riešenie:
Vzájomná poloha priamky a kužeľosečky sa zistí riešením sústavy ich rovníc, ktoré vedie na riešenie kvadratickej rovnice. Ak
D > 0 priamka je sečnica
D = 0 priamka je dotyčnica
D < 0 priamka je nesečnica
Ak bod T[ xT; yT] je bod dotyku ležiaci na kužeľosečke aj priamke platí:
Rovnice dotyčníc :
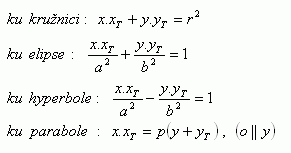
2. Zistite vzájomnú polohu priamky 2x +y – 8 = 0 a paraboly x2 +8y = 0
Riešenie:

3.Zistite vzájomnú polohu priamky x + y – 10 = 0 a elipsy x2 + 3y2 – 3 = 0
Riešenie:

4.Vyšetrite vzájomnú polohu kružnice k: x2 + y2 -25 = 0 a priamky p:
Riešenie:
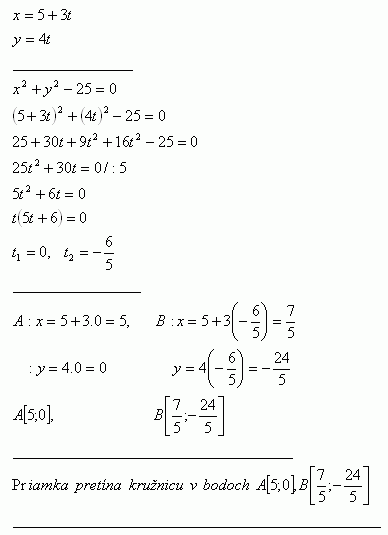
5.Určite c tak, aby priamka x – y + c = 0 boka dotyčnicou paraboly y2 = 6x
Riešenie:
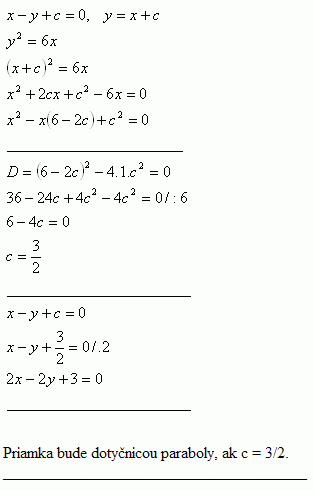
6. Určite k tak, aby priamka y = kx + 3 bola dotyčnicou k hyperbole 16x2 – 25y2 - 400 = 0
Riešenie:

7. Napíšte rovnice dotyčníc ku kružnici x2 + y2 = 25 v jej dotykovom bode T [3;y]. Zistite aj uhol φ medzi dotyčnicami.
Riešenie:
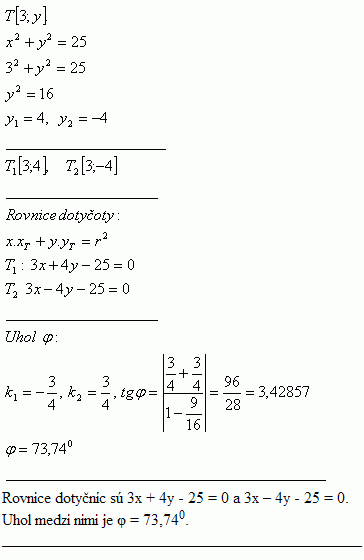
8.Napíšte rovnicu dotyčnice ku parabole y2 = 18x, ktorá je rovnobežná s priamkou p : 3x – 4y + 69 = 0
Riešenie:
Bod dotyku T [xT ; yT] :
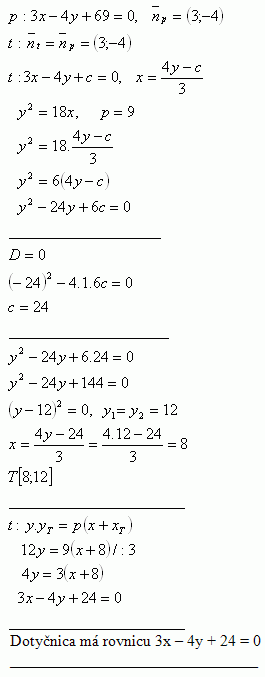
9.Určite dĺžku tetív, ktoré postupne vytína kružnica na súradnicových osiach, ak rovnica kružnice je x2 + y2 – 8x + 7y +12 = 0
Riešenie:
Priesečníky s osou x ( y = 0 ):
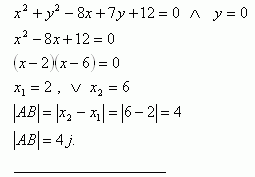
Priesečníky s osou y ( x = 0):
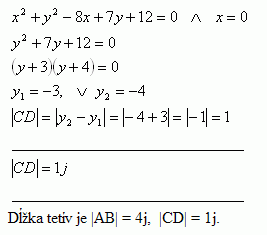
10.Ktorá dotyčnica elipsy E: x2 + 4y2 -16 = 0 je rovnobežná s priamkou p:
Riešenie: