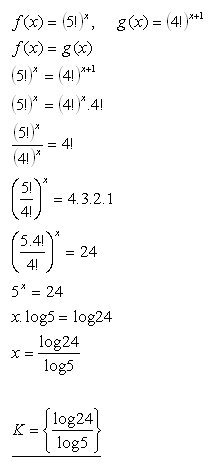Vlastnosti funkcií
1. Čo si pamätáte o vlastnostiach funkcií?
Riešenie:
Funkcia f reálnej premennej x je predpis, ktorý každému x e R priraďuje najviac jedno y e R tak, že
y = f(x)
Definičný obor funkcie D je množina všetkých x e R, ku ktorým existuje práve jedno y e R tak, že
y = f(x).
Obor hodnôt funkcie H je množina všetkých y e R, ku ktorým existuje aspoň jedno x e R tak, že
y = f(x).

Dve funkcie sa rovnajú : f(x) = g(x) ak: D(f) = D(g)
f(x) = g(x)
Ktoré z nasledujúcich grafov predstavujú funkcie?
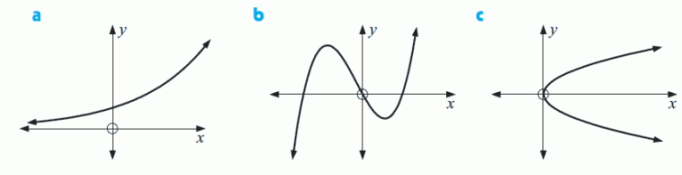
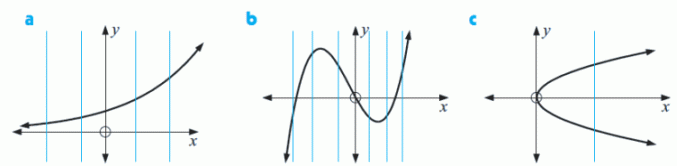
Funkcia Funkcia Nie je funkcia
2.Zistite, či nasledujúce výrazy sú funkcie:
Riešenie:
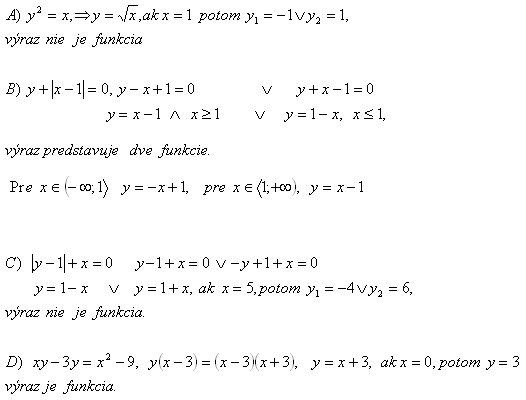
3.Rozhodnite, či nasledujúce funkcie sa rovnajú:
Riešenie:
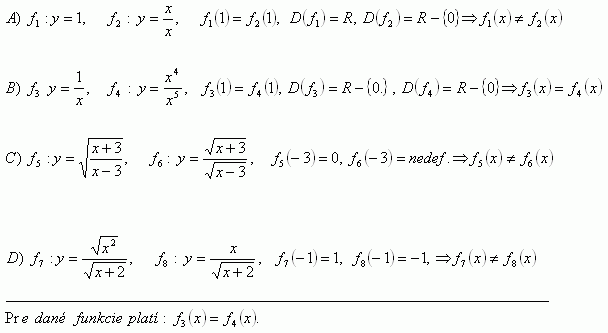
4.Rozhodnite o párnosti a nepárnosti funkcií:
Riešenie:
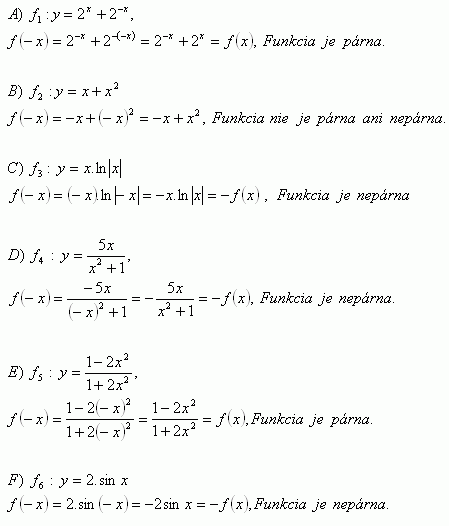
5. Zistite, ktoré z nasledujúcich funkcií sú ohraničené v danom definičnom obore.
Riešenie:

6. K daným funkciám vytvorte inverzné funkcie.
Riešenie:
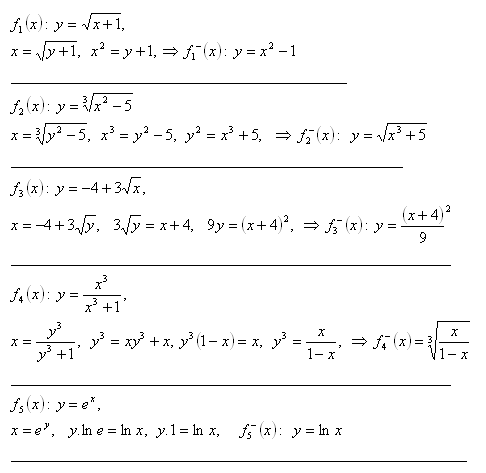
7. Určite inverznú funkciu k funkciám:
Riešenie:
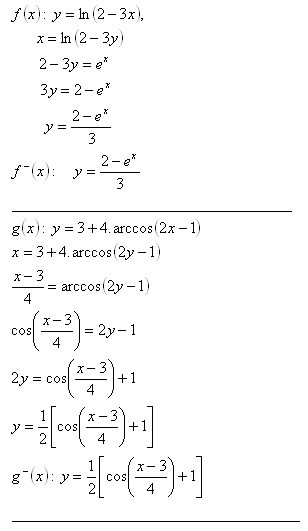
8.Vo funkcii f(x) : y = ax2 +bx +c , x e R, určite a,b,c e R tak aby platilo f(0) = -3, f(-1) = -6, f(2) = 15.
Riešenie:
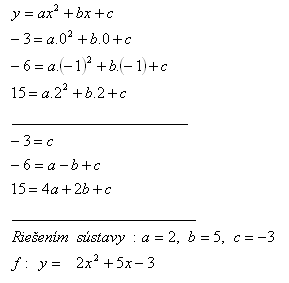
9. Určite b , d funkcie f: y = ( x +b ):( x +d) tak, aby platilo f(1) = -1, f(-1) = -1/3
Riešenie:
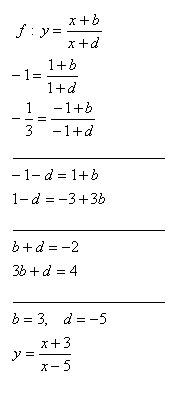
10. Určite množinu všetkých funkcií f(x), pre ktoré platí:
Riešenie:

11.Daná je funkcia f: y= -2x +3
a.) Určite f(0), f(-5)
b.) Pre ktoré x platí f(x) = 1, f(x) =-5
c.) Určite priesečník grafu funkcie so súradnicovými osami
Riešenie:
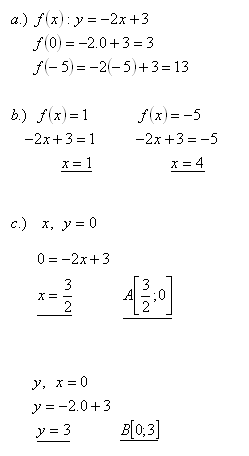
12.Napíšte lineárnu funkciu, ktorej graf prechádza bodmi
Riešenie:
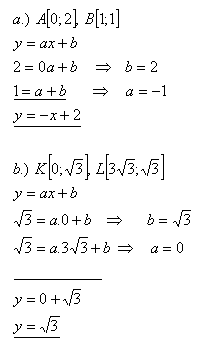
Rovnice funkcií sú: f1: y = – x + 2 a f2: y = √3.
13.Podľa výrobcu automobilu je spotreba benzínu auta na 100 km nasledujúca. Pri rýchlosti 80 km.h-1 6 litrov benzínu, pri rýchlosti 110 km.h-1 8,1 litra. Určite spotrebu auta pri rýchlosti 90 km.h-1.
Riešenie:
x = rýchlosť, y = spotreba
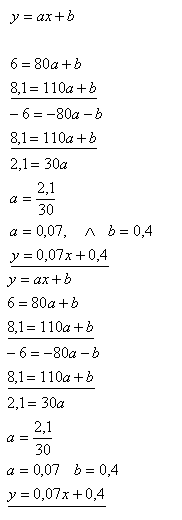
Spotreba pri rýchlosti 90 km.h-1.
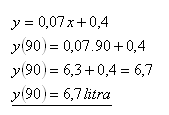
Spotreba automobilu pri rýchlosti 90 km.h-1 je 6,7 litra benzínu na 100 kilometrov.
14.Daná je funkcia f: y = x2 - 4x -12.
a.) Určite pre ktoré x platí f(x) = 9
b.) Určite priesečníky grafu funkcie so súradnicovými osami
Riešenie:
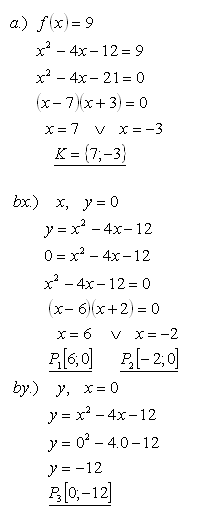
15.Napíšte kvadratickú funkciu , ktorej prvkami sú usporiadané dvojice
A[0;1], B[2;-1], C[1;-1]
Riešenie:
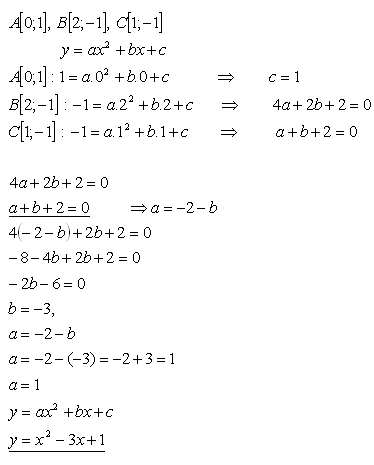
Kvadratická funkcia má rovnicu: f : y = x2 - 3x +1
16.Daná je kvadratická funkcia f: y = x2 – 3x + c. Určite c tak, aby funkcia
a.) nemala spoločný bod s osou x
b.) mala práve jeden spoločný bod s osou x
c.) mala práve dva spoločné body s osou x
Riešenie:
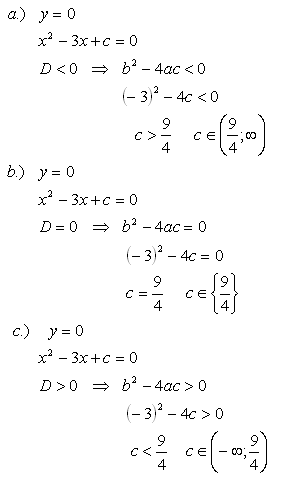
17.Daná je kvadratická funkcia f: y = x2 + 4x – 5. Určite jej priesečníky so súradnicovými osami a vrchol jej parabolického grafu.
Riešenie:
S osou x: y = 0 S osou y : x = 0

18.Určite koeficienty a, b tak, aby graf funkcie f: y = a.log x +b prechádzal bodmi K, L ak platí:
Riešenie:
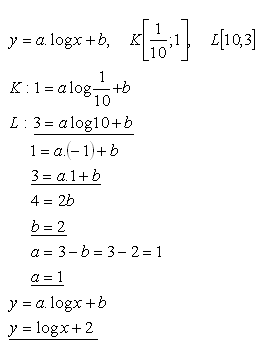
Rovnica logaritmickej funkcie má tvar: y = log x +2.
19.Určite koeficienty a, b tak, aby funkcia f: y = a2x + b prechádzala počiatkom súradnicovej sústavy a bodom M [1; 1].
Riešenie:
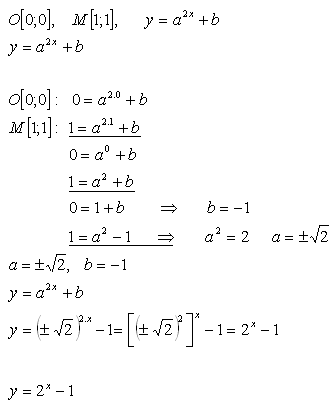
Funkcia má tvar f: y = 2x - 1.
20.Pre ktoré reálne čísla x nadobúdajú funkcie f(x) = (5!)x a funkcia g(x) = (4!)x+1 rovnaké hodnoty?
Riešenie: