Atómový obal
1. Ako vyzerá atóm?
Riešenie:
Aristoteles (384 p.n.l): Hmota je spojitá, dá sa deliť donekonečna. Leukipos , Demokritos (5. stor. p.n.l): Hmota je nespojitá, skladá sa z ďalej nedeliteľných častíc – atómov. J.J.Thomson (1856–1940) vytvoril t.z.v model „hrozienkového koláča“. Atóm je kladne nabitá guľa v ktorej sa vznášajú elektróny. E.Rutherford (1871–1937). Vytvoril „planetárny model atómu“. Celá hmotnosť atómu (tiež jeho kladný náboj) je sústredený v jadre (10–15m). Okolo jadra po kružnici (elipse – A. Sommerfeld) obiehajú elektróny . Polomer atómu je asi 10–10m. Hlavným nedostatkom tohto modelu bolo, že pri obiehaní elektrónu okolo jadra, by elektrón strácal energiu, jeho rýchlosť by sa zmenšovala, pohyboval by sa po špirále a padol by na jadro. Hmotný svet by nemohol existovať. N. Bohr (1883–1962) vytvoril „kvantový model atomu“.
- a.) Elektrón sa môže pohybovať okolo jadra len po celkom určitých kruhových dráhach, ktoré sa volajú orbitály (energetické hladiny) Dĺžka orbitálu sa rovná celočíselnému násobku vlnovej dĺžky de Broglieho vlny, prislúchajúcej elektrónu.
- b.) Ak sa elektrón pohybuje po orbitále, nevyžaruje energiu
- c.) Pri prechode elektrónu z jedného orbitálu na ktorom mal energiu En, na druhý orbitál s menšou energiou Em , vyžiari jedno svetelné kvantum – fotón K. Heisenberg (1901-1976), E. Schrodinger (1887–1961) vytvorili „kvantovo mechanický, pravdepodobnostný model“ Nie je možné rovnako presne určiť polohu elektrónu a súčasne jeho rýchlosť. Dajú sa určiť miesta, kde sa môže elektrón s určitou pravdepodobnosťou v priestore okolo jadra nachádzať
2. Aké vlastnosti má atóm vodíka v Bohrovom modele?
Riešenie:

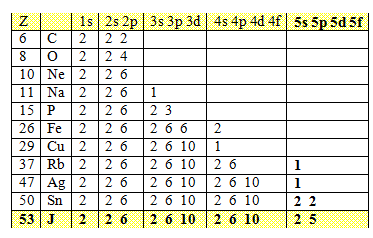
Obsadenie dráh elektrónového obalu niektorých atómov:
3.Za aký čas preletí svetlo atómom s polomerom r = 3.10–10m
Riešenie:
Rozbor:
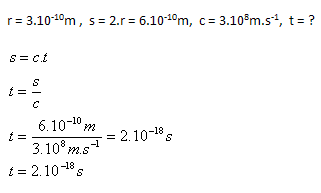
Svetlo preletí atómom za čas t = 2.10–18s.
4. Vypočítajte energiu základného stavu atómu vodíka E1. 1J = 0,6242.1019 eV
Riešenie:

Energia základného stavu atómu vodíka je E1 = -13,6eV.
5.Vypočítajte energie atómu vodíka na stacionárnych dráhach s hlavným kvantovým číslom n = 1,2,3,4,5,6. Energia na prvej kvantovej dráhe je E1 = -13,6 eV. (príklad 4)
Riešenie:
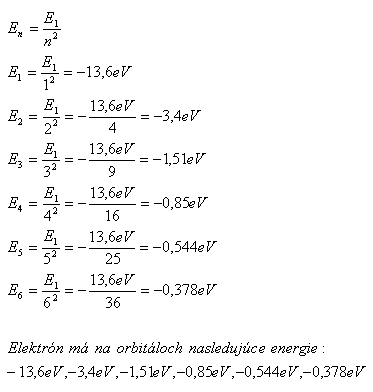
6.Vypočítajte rýchlosti pohybu elektrónu na jednotlivých orbitáloch v atóme vodíka, ak viete že
r1 = 0,53.10–10m.
Riešenie:
Rozbor:
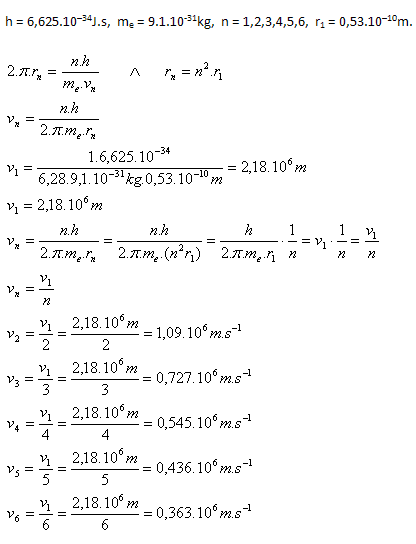
7.Určite frekvenciu viditeľných čiar Balmerovej série (J.Balmer, 1825-1898) pre vodík. Séria vznikne preskokmi elektrónov na druhú kvantovú dráhu.
Riešenie:
Rozbor:
E1 = –13,6eV, E2 = –3,4eV, E3 = –1,5eV,
E4 = –0,85eV, E5 = –0,544eV, E6 = – 0,378eV
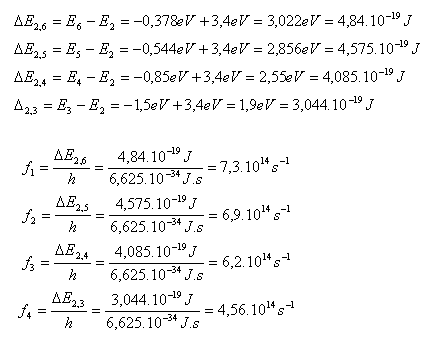
8.Atóm vodíka, ktorý je v základnom stave, získal energiu 10,2eV. Na ktorú energetickú hladinu pri tom prešiel elektrón?
Riešenie:
Rozbor:
ΔE = 10,2eV, E1 = –13,6eV, n = ?
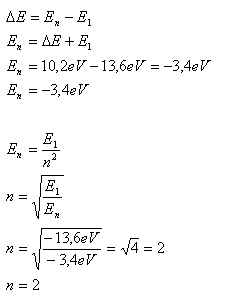
Elektrón prešiel na druhú energetickú hladinu.
9. Héliovo – neónový laser má výkon 2mW a vysiela žiarenie vlnovej dĺžky 632,8nm. Určite energiu, hmotnosť a hybnosť emitovaných fotónov.
Riešenie:
Rozbor:
P = 2.10-3W, λ = 632,8.10-9m, E = ?, m = ?, p = ?
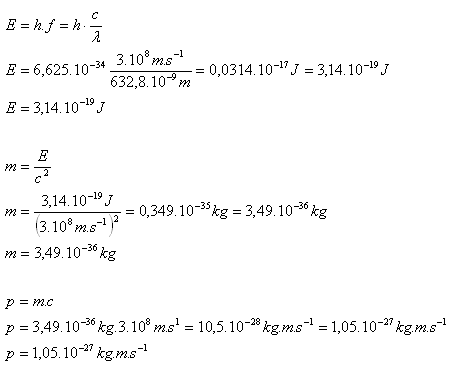
Fotón má energiu E = 3,14.10-18J, hmotnosť m = 3,49.10-36kg a impulz p = 1,05.10-27kg.m.s-1.
10.Atóm vodíka prejde zo stacionárneho stavu n = 6 do stavu m = 1 Vypočítajte frekvenciu a vlnovú dĺžku vyžiareného fotónu. Použite Rydbergov zákon. (J.R. Rydberg 1854-1919)
Riešenie:
Rozbor:
n = 6, m = 1, R = 3,29.1015s-1
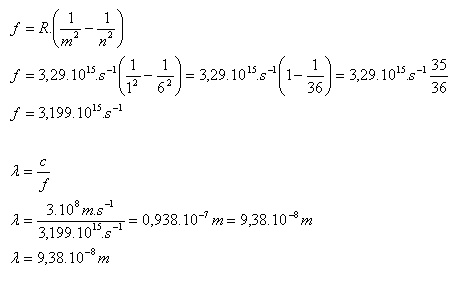
Vyžiarený fotón má frekvenciu f = 3,199.1015 Hz a vlnovú dĺžku λ = 9,38.10–8m.
11.Vypočítajte veľkosť elektromagnetickej energie, ktorú vyžiari atóm vodíka, ak jeho elektrón preskočí z prvého orbitálu na nekonečne vzdialený orbitál.
Riešenie:
Rozbor:
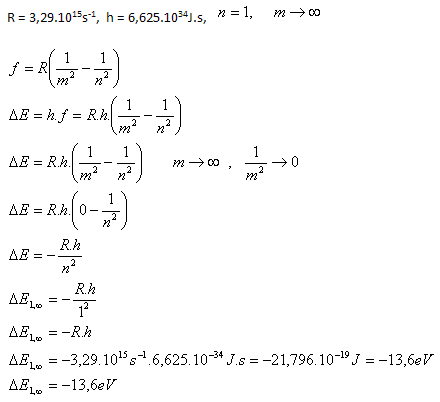
Atóm vodíka vyžiari –13,6eV elektromagnetickej energie.
12.Odvoďte Rydbergovu konštantu R
Riešenie:
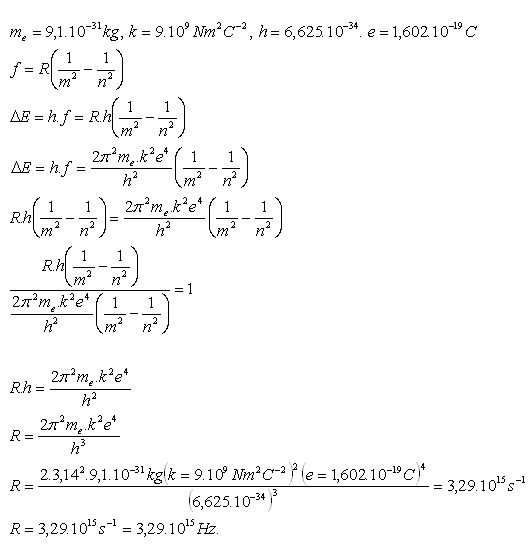
13.Určite tri najdlhšie vlnové dĺžky Balmerovej série. Táto séria zodpovedá vyžarovaniu energie elektrónu pri prechode 3 – 2, 4 – 2, 5 – 2.
Riešenie:

Najdlhšie vlnové dĺžky Balmerovej série zodpovedajú farbám červenej, modrej a fialovej.
14.Aké napätie musí byť v elektrickom poli, ak v ňom máme urýchliťelektrón tak, aby mohol pri zrážke s atómom vodíka previesť atóm zo základného stavu do prvého excitovaného stavu.
Riešenie:
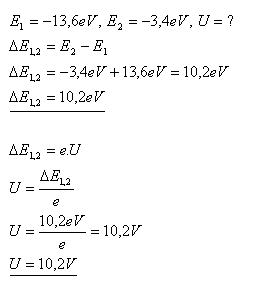
Napätie v elektrickom poli musí byť U = 10,2V.
15.Polomer prvej kružnicovej dráhy elektrónu v atóme vodíka je r = 0,53.10–10m. Určite intenzitu elektrického poľa od jadra na tejto dráhe.
Riešenie:
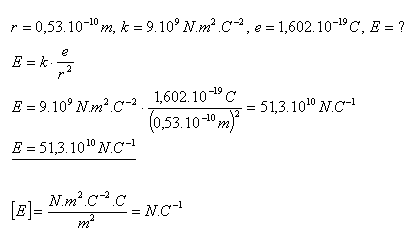
Intenzita elektrického poľa na prvej dráhe elektrónu v atóme vodíka je E = 51,3.1010N.C–1.
16.Aký veľký je potenciál jadra atómu na prvej dráhe elektrónu v atóme vodíka?
(E = 51,3.1010N.C–1 – príklad 15)
Riešenie:
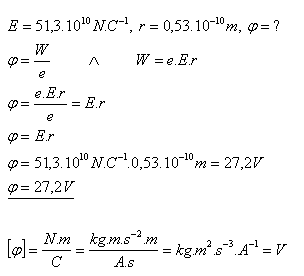
Potenciál na prvej dráhe elektrónu v atóme vodíka je φ = 27,2V.
17.Zistite, či môže nastať fotoelektrický jav pri dopade viditeľného svetla na zinok WV(Zn) = 4eV. Najkratšia vlnová dĺžka viditeľného svetla je λ = 390nm.
Riešenie:
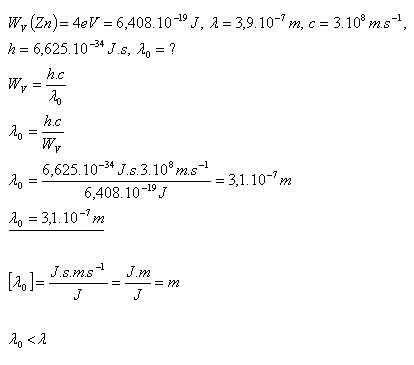
Fotoemisia nenastane lebo λ0 < λ.
18.Výstupná práca z platiny je WV(Pt) = 5,29eV. Vypočítajte medzný kmitočet f0, pri ktorom nastane fotoelektrický jav.
Riešenie:
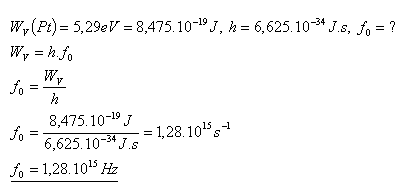
Medzný kmitočet pri ktorom nastane fotoelektrický jav je f0 = 1,28.1015Hz.
19.Akou rýchlosťou vystupujú elektróny z povrchu cézia, ak jeho povrch osvetlíme monochromatickým svetlom s vlnovou dĺžkou λ = 590nm. Výstupná práca cézia je WV(Cs) = 1,93eV
Riešenie:
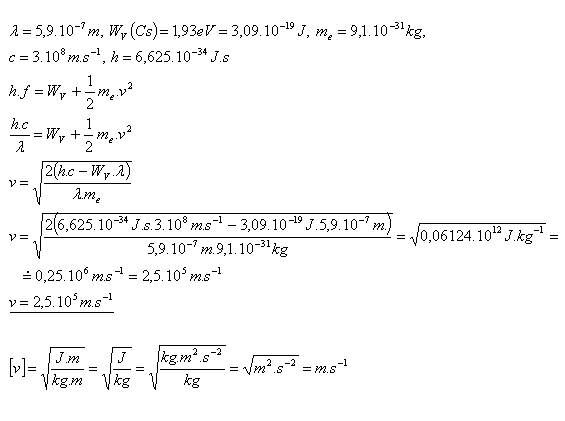
Elektróny z povrchu cézia vystupujú rýchlosťou v = 2,5.105m.s–1.
20.Odvoďte vzťah pre výpočet energie elektrónu, ktorý je viazaný na úsečku dĺžky L.
Riešenie:
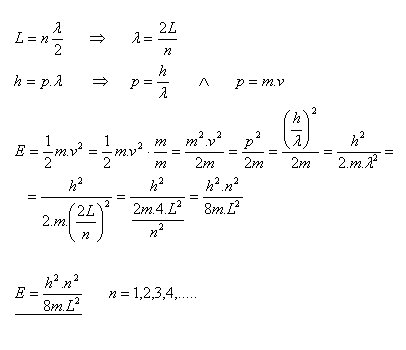
21.Aká bude energia základného a prvého excitovaného stavu elektrónu viazaného na úsečku L = 4.10–10m
Riešenie:
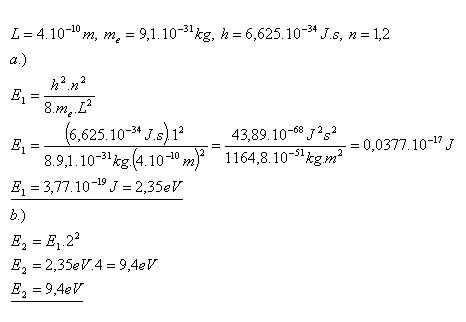
Energie elektrónu sú E1 = 2,35 eV, E2 = 9,4 eV.
22.Akú dĺžku musí mať úsečka, na ktorú je viazaný elektrón, aby rozdiel energií základného a prvého excitovaného stavu bol menší ako 3 eV.
Riešenie:
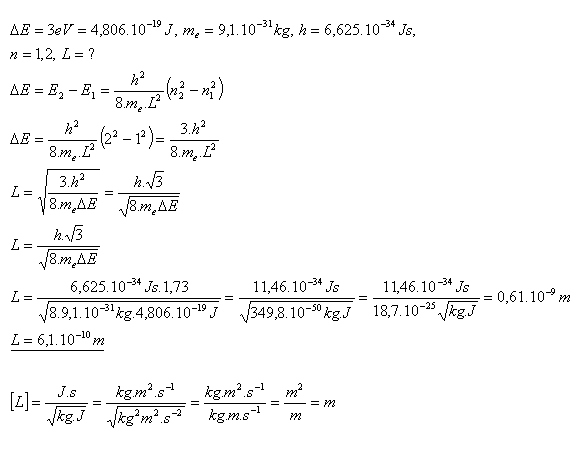
Dĺžka úsečky musí byť asi L = 6.10–10m
23.Akú elektrónovú konfiguráciu má atóm sodíka, železa, medi a striebra? Použite tabuľku v príklade č. 2.
Riešenie:
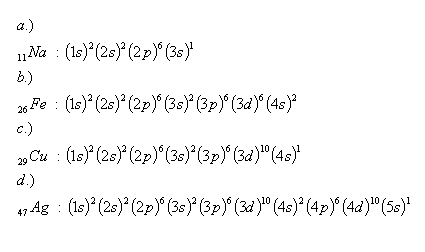
24. Ktoré prvky majú dané konfigurácie:
Riešenie:
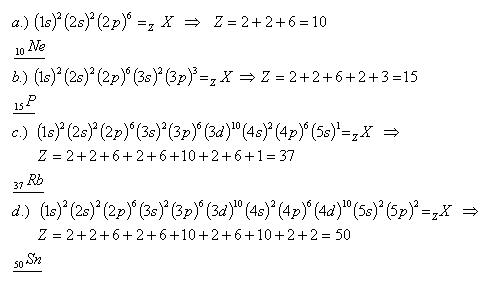
Sú to prvky neón, fosfor, rubídium a cín.
25.Určite energiu elektrónu v základnom stave molekuly butadiénu s konfiguráciou (1s)2(2s)2. Elektróny sa pohybujú po celej dĺžke L = 0,6.10–9m molekuly.
Riešenie:
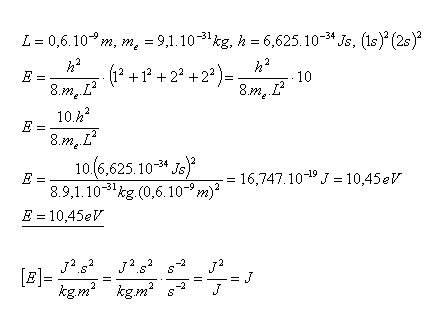
Energia elektrónu v základnom stave molekuly butadiénu je E = 10,45 eV.