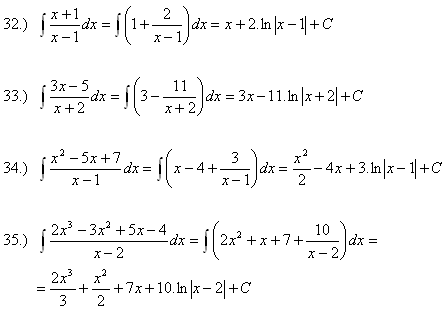Integrál - priama metóda
1. Zopakujte si základné vzorce integrovania priamou metódou
Riešenie:
Neurčitý integrál:
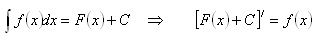
f(x) dx je integrand, F(x) je primitívna funkcia, C je integračná konštanta
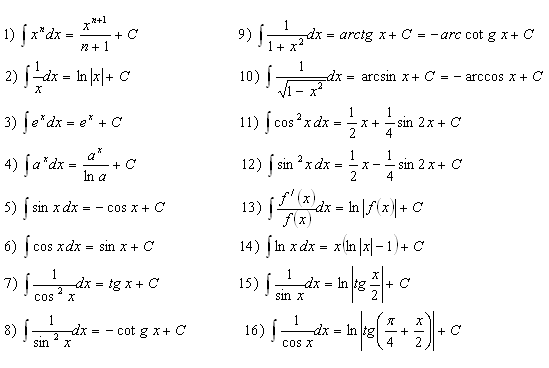
2. Vypočitajte integrály:
3.Vypočitajte integrály:
Riešenie:
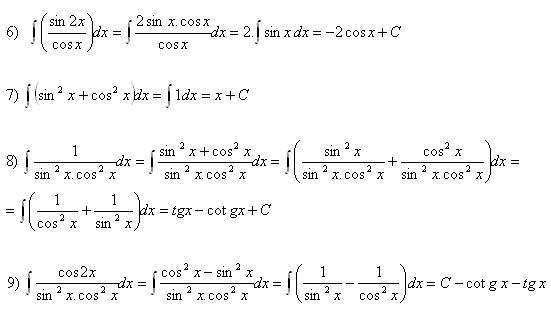
4.Vypočitajte integrály:
Riešenie:
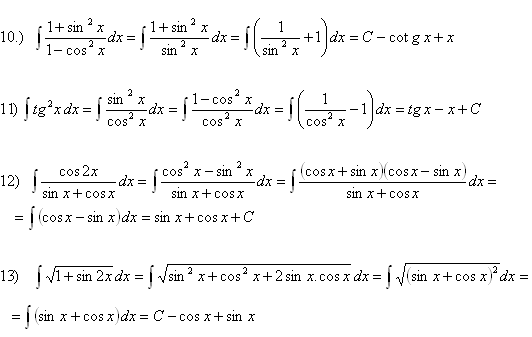
5. Vypočitajte integrály:
Riešenie:
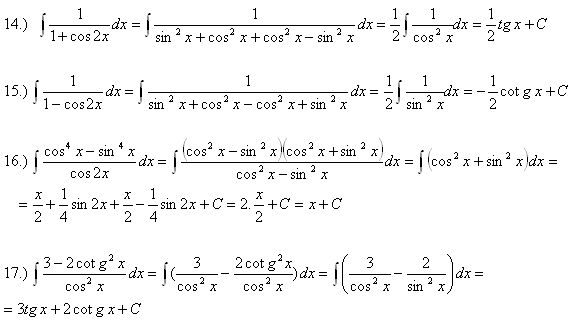
6.Vypočitajte integrály:
Riešenie:
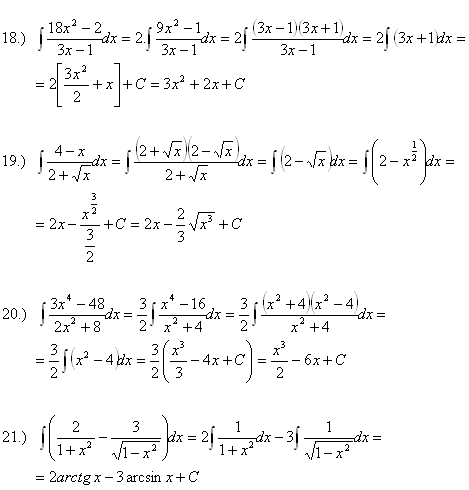
7.Vypočitajte integrály:
Riešenie:
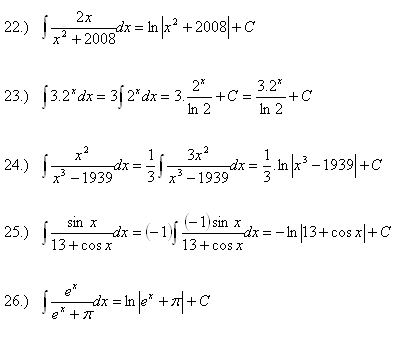
8.Vypočitajte integrály:
Riešenie:
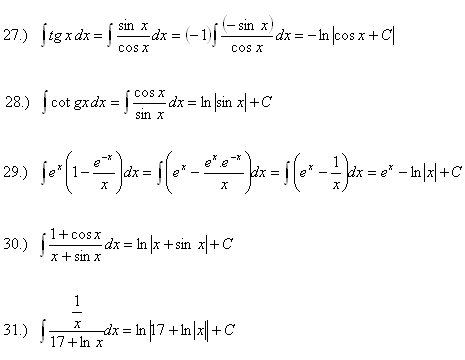
9.Vypočitajte integrály:
Riešenie: