Oxidačno- redukčné (redoxné) rovnice
Redukcia je proces, pri ktorom atóm znižuje svoje oxidačné číslo. Oxidácia je proces, pri ktorom atóm zvyšuje svoje oxidačné číslo. Zmena oxidačného čísla nastáva skutočným alebo formálnym odovzdávaním elektrónov (oxidácia), resp. prijímaním elektrónov (redukcia; elektróny majú záporný elektrický náboj, preto sa ich prijímaní oxidačné číslo znižuje).
Redukovadlo je reaktant, ktorý spôsobí redukciu iného reaktantu (aspoň jeden atóm redukovadla zvyšuje svoje oxidačné číslo). Oxidovadlo je reaktant, ktorý spôsobuje oxidáciu iného reaktantu (aspoň jeden atóm oxidovadla znižuje svoje oxidačné číslo).
Čiastková chemická rovnica vyjadruje len oxidáciu alebo len redukciu; v elektrochémii sa jej hovorí aj článková chemická rovnica.
Pri riešení redoxných rovníc dodržiavame všeobecné pravidlá na výpočet stechiometrických koeficientov používame nasledovný postup:
- Zistíme oxidačné čísla všetkých atómov v rovnici.
- Napíšeme čiastkovú chemickú rovnicu oxidácie a čiastkovú chemickú rovnicu redukcie.
- Matematicky upravíme čiastkové chemické rovnice oxidácie a redukcie tak, aby bolo zachované pravidlo bilancie počtu elektrónov.
- Obe čiastkové chemické rovnice sčítame a upravíme, pričom získame skrátenú redoxnú rovnicu (SRR).
- Získané počty atómov zohľadníme v chemickej rovnici pomocou stechiometrických koeficientov.
- Na základe pravidla bilancie počtu atómov priradíme stechiometrické koeficienty látkam obsahujúcim atómy, ktoré nezmenili oxidačné číslo.
- Ak ide o iónovú redoxnú rovnicu, na zistenie stechiometrických koeficientov využijeme pravidlo bilancie nábojových čísiel.
Jednoduché disproporcionačné a symproporcionačné redoxné chemické reakcie sú také chemické reakcie, pri ktorých sa mení oxidačné číslo atómov len jedného prvku; inak sa ničím nelíšia od ostatných redoxných reakcií.
Redoxné chemické rovnice, ktorých reaktanty obsahujú atómy daného prvku s jedným oxidačným číslom a produkty obsahujú atómy toho istého prvku s rozličnými oxidačnými číslami, nazývame disproporcionačné rovnice. Napríklad:
3ReVIF6 + 10H2O → 2HReVIIO4 + ReIVO2 + 18HF
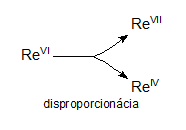
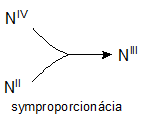
Redoxné chemické rovnice, ktorých reaktanty obsahujú atómy daného prvku s rozličnými oxidačnými číslami a produkty obsahujú atómy toho istého prvku len s jedným oxidačným číslom, nazývame symproporcionačné rovnice. Napríklad:
NIVO2 + NIIO + 2NaOH → 2NaNIIIO2 + H2O
1.Vyrovnajte oxidačno-redukčnú rovnicu:
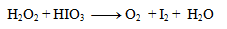
Riešenie:
Prvým krokom je určenie oxidačných stupňov atómov prvkov v každej zlúčenine:
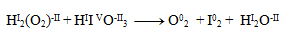
Oxidačné čísla teda menia iba jód a kyslík. Napíšeme pre ne polreakcie, t.j. reakcie v ktorých vystupujú iba daný oxidujúci/ redukujúci sa prvok a elektróny.
Oxidácia:
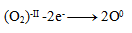
Redukcia:
2IV +10e- -------> 2I0
Následne vynásobíme rovnice tak, aby sa počty elektrónov vyrovnali:
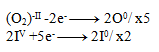
A rovnice spočítame:
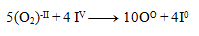
Takto získané koeficienty dosadíme do pôvodne rovnice a dorátame počet ostatných prvkov tak, aby sme dodržali zákon zachovania počtu atómov toho istého prvku. Výsledná rovnica má tvar:
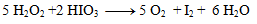
2.Doplňte stechimetrické koeficienty v redoxnej rovnici:
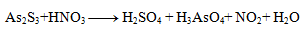
Riešenie:
Najpr je potrebné určít oxidačné čísla atómov všetkých reaktantov a produktov:
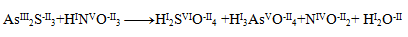
Môžeme si všímnúť, že jedine arzén, síra a dusík menia svoje oxidačné čísla. Pre tieto dva prvky napíšeme tzv. polreakcie, v ktorých zaznačíme aj počet vymieňaných elektrónov.
Rovnice oxidácie:
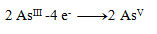
(na jeden arzén treba 2 elektróny)
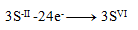
(na jednu síru treba 8 elektrónov)
Rovnica redukcie:
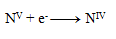
Ďalším krokom je úprava počtu vymieňaných elektrónov tak, aby sa menil rovnaký počet pri oxidáciách ako pri redukciách- teda pri všetkých troch polreakciách sa bude vymieňať 28 elektrónov. 24+4= 28 elektrónov pri oxidácii, toľko treba aj pri redukcii, preto
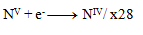
a teda
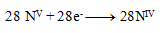
Stechiometrické koeficienty z polreakcií doplníme do rovnice a dopočítame ostatné prvky. Výsledná rovnica má tvar:
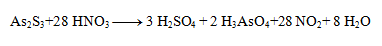
3. Vyčíslite nasledujúce redoxné rovnice:
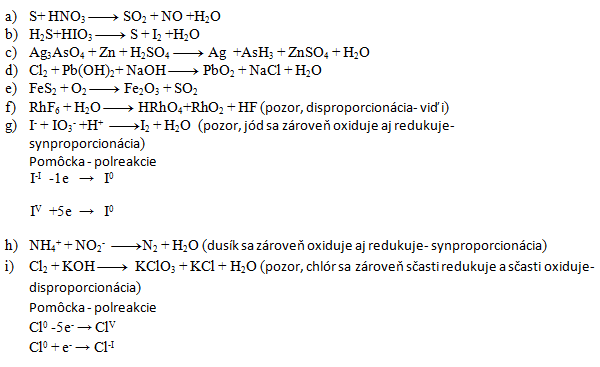
Riešenie:
- a) 3,4,3,4,2
- b) 5,2,5,1,6
- c) 2,11,11,6,2,11,8
- d) 1,1,2,1,2,2
- e) 4,11,2,8
- f) 3,10,2,1,18
- g) 5,1,6,3,3
- h) 1,1,1,2
- i) 3,6,1,5,3
4.Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici:
Cr + H2SO4 → Cr2(SO4)3 + H2
5. Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici:
Ca3(PO4)2 + SiO2 + C → P4 + CaSiO3 + CO
6.Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici:
MnO4– + Fe2+ + H3O+ → Mn2+ + Fe3+ + H2O
7. Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici:
Cu + HNO3 → Cu(NO3)2 + NO2 + H2O
8. Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici:
KMnO4 + HBr → Br2 + MnBr2 + KBr + H2O
9. Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici:
ReF6 + H2O → HReO4 + ReO2 + HF
10.Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici:
MnO42– + H3O+ → MnO4– + MnO2 + H2O
11. Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici:
NO2 + NO + NaOH → NaNO2 + H2O
12. Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici:
I– + IO3– + H3O+ → I2 + H2O
13. Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici (Náročnejší príklad pre chemickú olympiádu):
FeS2 + O2 → Fe2O3 + SO2
14.Zistite stechiometrické koeficienty v nasledujúcej chemickej rovnici (Náročnejší príklad pre chemickú olympiádu):
Au + KCN + O2 + H2O → K[Au(CN)2] + KOH