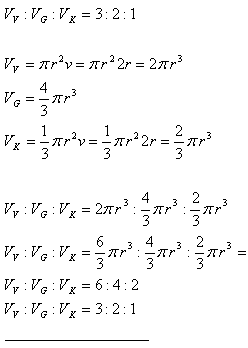Dôkazy
1. Ako dokazujeme pravdivosť matematickej vety?
Riešenie:

2.Priamym dôkazom dokážte vetu:
Riešenie:
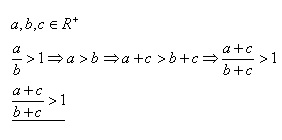
Čo platí podľa predpokladu.
3.Priamym dôkazom dokážte vetu:
Riešenie:
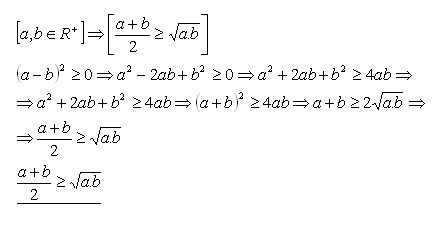
Platí pre všetky a,b z R+
4.Priamym dôkazom dokážte vetu:
Riešenie:
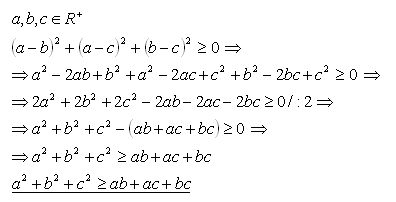
Platí vždy, lebo súčet troch štvorcov troch reálnych čísiel je vždy kladný. Rovnosť platí ak a = b = c.
5.Priamym dôkazom dokážte vetu:
Riešenie:
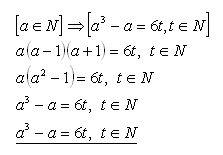
Veta platí. Z troch za sebou idúcich prirodzených čísiel (a – 1), a, (a + 1), jedno je deliteľné 2 a jedno deliteľné 3. Teda ich súčin je deliteľný 6.
6.Nepriamym dôkazom dokážte vetu: Ak a2 je prirodzené číslo deliteľná 3, potom aj a je prirodzené číslo deliteľná 3.
Riešenie:
B‘ => A‘:
Ak a nie je deliteľné tromi, potom aj a2 nie je deliteľné 3.
1) a = 3k + 1
a2= (3k + 1 )2
a2= 9k2 +6k +1
a2= 3(3k2 + 2k) +1
a2= 3m + 1 – platí m = 3k2 +2k
2) a = 3k + 2
a2= (3k + 2)2
a2= 9k2 +12k +4
a2= 3(3k2 +4k +1) +1
a2= 3m +1 – platí m = 3k2 + 4k +1
Tým sme dokázali, že pôvodná veta platí.
7.Nepriamym dôkazom dokážte vetu: pre prirodzené číslo a platí: Ak a4 + 2 nie je deliteľné 3, potom a je deliteľné 3.
Riešenie:
B‘ => A‘:
Ak a nie je deliteľné 3, potom a4 + 2 je deliteľné 3
1)
a = 3k + 1
a4 +2 = (3k +1)4 +2
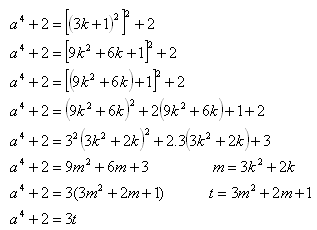
Pre a = 3k +2 spravte dôkaz sami .
Pôvodná veta platí.
8.Dokážte sporom vetu: Pre všetky kladné reálne čísla a, b platí:
Dôkaz:
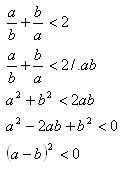
Negovaná veta neplatí pre žiadne kladné reálne čísla. Platí pôvodná veta.
9.Dokážte sporom vetu : Číslo √3 je iracionálne
Riešenie:
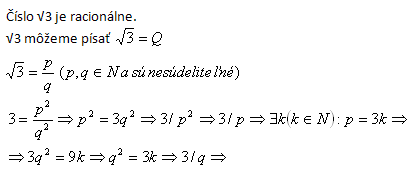
Číslo p je deliteľné 3, číslo q je deliteľne 3, teda nie sú nesúdeliteľné. Predpoklad, že √3 je racionálne číslo neplatí. Platí pôvodná veta, že √3 je iracionálne, čo bolo treba dokázať.
10. Matematickou indukciou dokážte vetu: Pre všetky prirodzené čísla n platí:
Riešenie:
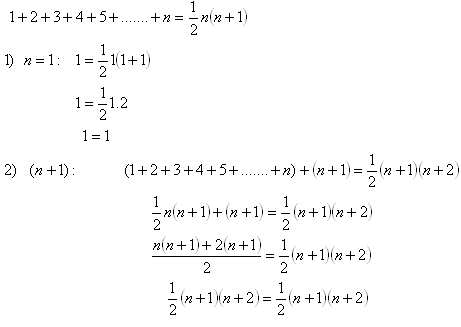
Tým sme dokázali pravdivosť vety pre všetky prirodzené čísla n.
11.Matematickou indukciou dokážte vetu: Pre všetky prirodzené čísla n platí:
Riešenie:
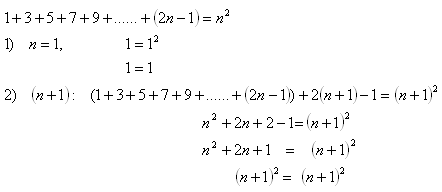
Tým sme dokázali pravdivosť vety pre všetky prirodzené čísla n.
12.Matematickou indukciou dokážte vetu: Pre každé prirodzené číslo n platí:
Riešenie:
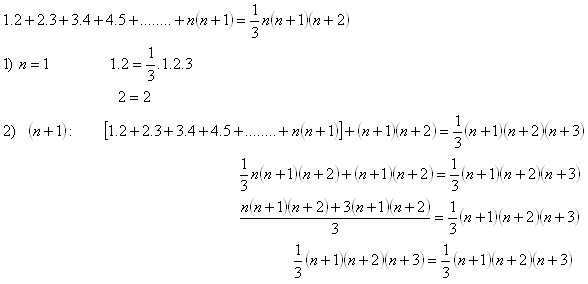
Tým sme dokázali pravdivosť vety pre všetky prirodzené čísla n.
13. Matematickou indukciou dokážte vetu: Pre každé prirodzené číslo n platí:
Riešenie:
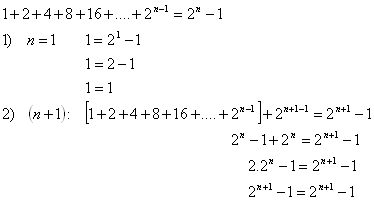
Tým sme dokázali pravdivosť vety pre všetky prirodzené čísla n.
14.Matematickou indukciou dokážte vetu:
Riešenie:
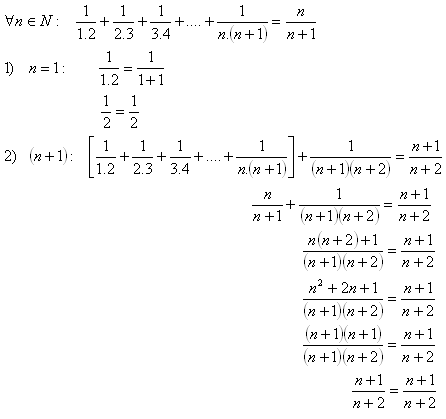
Tým sme dokázali pravdivosť vety pre všetky prirodzené čísla n.
15.Matematickou indukciou dokážte vetu:
Riešenie:
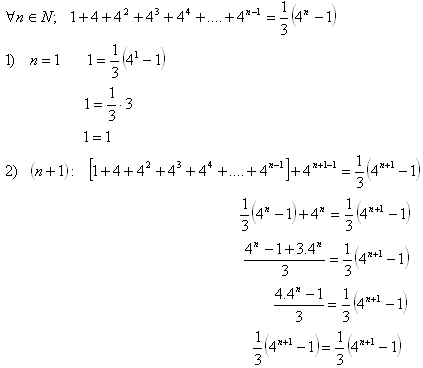
Tým sme dokázali pravdivosť vety pre všetky prirodzené čísla n.
16.Matematickou indukciou dokážte Moivreovu vetu
Riešenie:
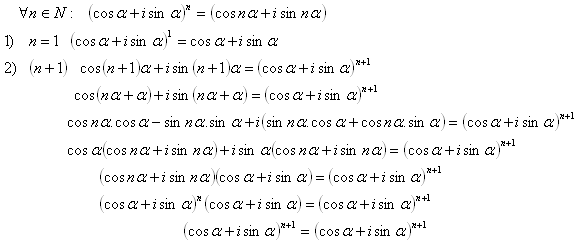
Tým sme dokázali vetu pre všetky prirodzené čísla.
17.Vo vnútri trojuholníka Δ ABC je daný bod U. Dokážte, že platí vzťah
Riešenie:
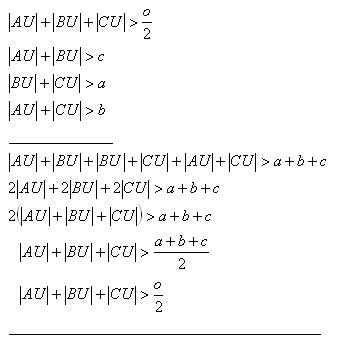
18.Dokážte vetu: Ťažnica trojuholníka je menšia ako polovica obvodu.
Riešenie:
V trojuholníku Δ ABC je |AB| = c, |AC| = b, |BC| = a. Bod S je stred strany a. |BS| = |SC| = a /2 . Ťažnica na stranu a je ta = |AS|.
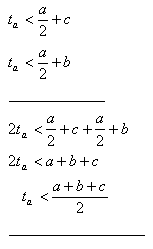
19.Dokážte vetu:
Riešenie:
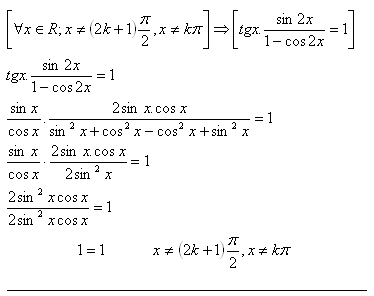
20.Rovnostrannému valcu je vpísaná guľa a kužeľ. Podstava kužeľa je zhodná s podstavou valca, vrchol kužeľa je v strede druhej podstavy. Ukážte, že Archimedova úloha platí. (Archimedes asi 287–212 pred n. l.)
Riešenie: