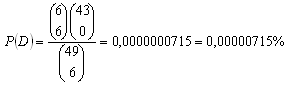Pravdepodobnosť
1. Definujte a charakterizujte pravdepodobnosť.
Riešenie:
a)
Klasická definícia pravdepodobnosti
Nech náhodný pokus spĺňa predpoklady
- počet všetkých výsledkov je konečný
- všetky výsledky sú rovnako možné
- žiadne dva výsledky nemôžu nastať súčasne
Pravdepodobnosť javu A je číslo
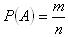
, kde n je počet všetkých možných výsledkov náhodného pokusu a m je počet všetkých priaznivých výsledkov, t.j. výsledkov, pri ktorých nastane jav A.
Platí : 0 ≤ P(A) ≤ 1
Pravdepodobnosť nemožného javu : P(A) = 0
Pravdepodobnosť istého javu: P(A) = 1
b)
Podmienená pravdepodobnosť udalosti A za podmienky B je číslo:
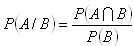
c)
Pravdepodobnosť nezávislých javov:
P(A∩B) = P(A)P(B)
d)
Pravdepodobnosť nezlučiteľných javov:
P(AUB) = P(A) + P(B)
e)
Binomické rozdelenie pravdepodobnosti:
Nech A je jav s pravdepodobnosťou P. Potom pravdepodobnosť, že pri n-násobnom opakovaní pokusu, jav A nastane práve k- krát je číslo:
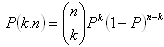
f)
Hypergeometrické rozdelenie pravdepodobnosti.
Nech V predmetov vybraných z N predmetov má určitú vlastnosť, potom N-V predmetov túto vlastnosť nemá.
Pravdepodobnosť, že práve k predmetov spomedzi n náhodne vybraných predmetov túto vlastnosť má, je číslo:
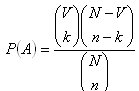
2. Z osemnástich lístkov očíslovaných 1 - 18 vytiahneme náhodne jeden lístok. Aká je pravdepodobnosť, že na vytiahnutom lístku bude:
a) párne číslo
b) číslo deliteľné 3
c) prvočíslo
d) deliteľné 6
Riešenie:
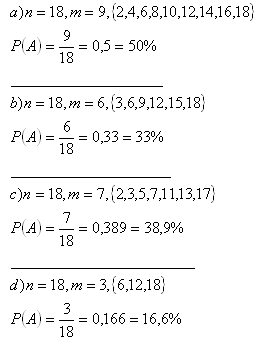
3. Aká je pravdepodobnosť že pri hode dvoma kockami (červenej a modrej) padne:
a) súčet 8
b) súčet, ktorý je deliteľný piatimi
c) súčet, ktorý bude párny
Riešenie:
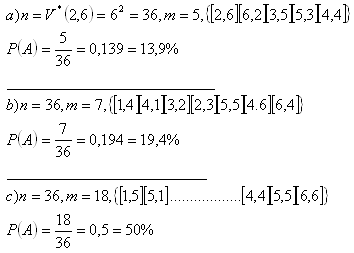
4. Hazardný hráč hádžuci tromi kockami, položil G. Galileiovi otázku : „Mám staviť na súčet 11 alebo súčet 12?“ Čo mu Galilei odpovedal?
Riešenie:
a) Súčet 11
n = V*(3,6) = 63 = 216
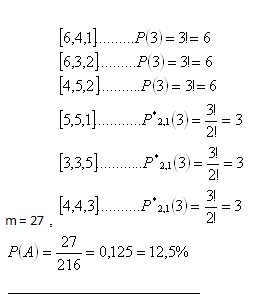
b) Súčet 12
n = V*(3,6) = 63 = 216
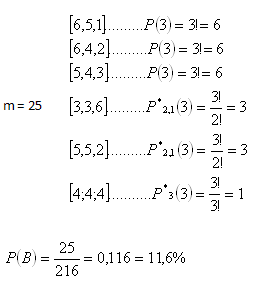
G. Galilei doporučil vsadiť na súčet 11, lebo P(11) > P(12).
5. Dlhodobé výskumy na istom území ukázali, že zo 100 000 detí sa 82 170 dožije 40 rokov a 37 930 sa dožije 70 rokov. Aká je pravdepodobnosť, že človek, ktorý sa dožije 40 rokov, dožije sa aj 70 rokov?
Riešenie:
(Ide o podmienenú pravdepodobnosť)
A – dožiť sa 70 rokov, P(A) = 0,3793
B – dožiť sa 40 rokov, P(B) = 0,8217
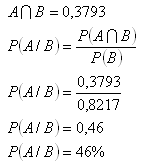
Pravdepodobnosť, že sa človek dožije 70 rokov je 46%.
6. V meste sú štyri križovatky so svetelnými semafórmi. Každý z nich uvoľňuje alebo uzatvára dopravu s rovnakou pravdepodobnosťou 0,5. Aká je pravdepodobnosť, že auto:
a) prejde prvou križovatkou bez zdržania
b) prejde prvými dvomi križovatkami bez zdržania
c) prejde všetkými štyrmi križovatkami bez zdržania
Riešenie:
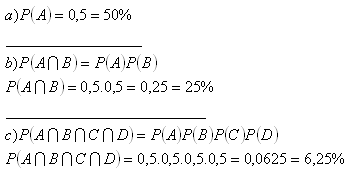
7. V 32 hracích kartách sú 4 esá a 12 figúr (4 králi, 4 horníci a 4 dolníci). Aká je pravdepodobnosť, že náhodne vytiahnutá jedna karta bude eso alebo figúra?
Riešenie:
Ide o pravdepodobnosť nezlučiteľných javov
A – vytiahnutá karta ja eso
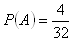
B - vytiahnutá karta je figúra
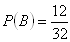
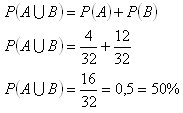
Pravdepodobnosť, že vytiahnutá karta bude eso alebo figúra je 50%.
8. Otcovia sú šťastní, keď sa im narodí syn. Z dlhodobých štatistík je známe, že pravdepodobnosť narodenia chlapca je P(A) = 0,51.
Otec si naplánoval 5 detí. Aká je pravdepodobnosť, že z týchto detí budú práve 3 synovia.
Riešenie:
Ide o binomické rozdelenie pravdepodobnosti.
n = 5, k = 3, P = 0,51
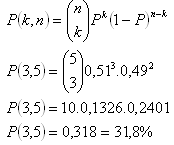
Otcovi sa prianie splní s pravdepodobnosťou 31,8 %.
9. V šestnástich fľašiach sú minerálky. Vieme, že v 10 fľašiach je Slatina a v 6 fľašiach je Baldovská. Aká je pravdepodobnosť, že medzi 4 náhodne vybratými fľašami sú 2 Slatiny a 2 Baldovaké?
Riešenie:
Ide o hypergeometrické rozdelenie pravdepodobvosti.
N = 16 (počet všetkých fliaš)
V = 10 (počet fliaš Slatiny)
N-V = 6 (počet fliaš Baldovskej)
n = 4 (počet náhodne vybratých fliaš)
k = 2 (vybraté Slatiny)
n – k = 2 (vybraté Baldovské)
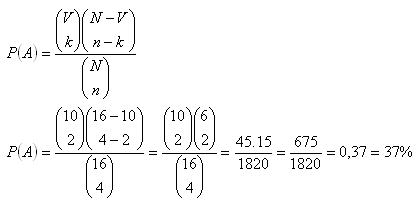
Predpoklad bude splnený s pravdepodobnosťou P(A) = 37 %.
10. V hazardnej číselnej hre sa losuje 6 čísiel zo 49 čísiel. Aká je pravdepodobnosť získať:
a) štvrté poradie
b) tretie poradie
c) druhé poradie
d) prvé poradie
Riešenie:
a) Štvrté poradie (uhádnuť 3 čísla zo 6 vylosovaných)
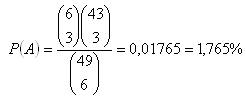
b) Tretie poradie (uhádnuť 4 čísla zo 6 vylosovaných)
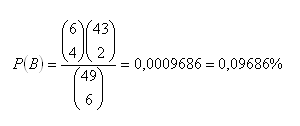
c) Druhé poradie (uhádnuť 5 čísiel zo 6 vylosovaných)
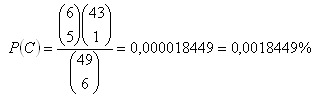
d) Prvé poradie (uhádnuť 6 čísiel zo 6 vylosovaných)