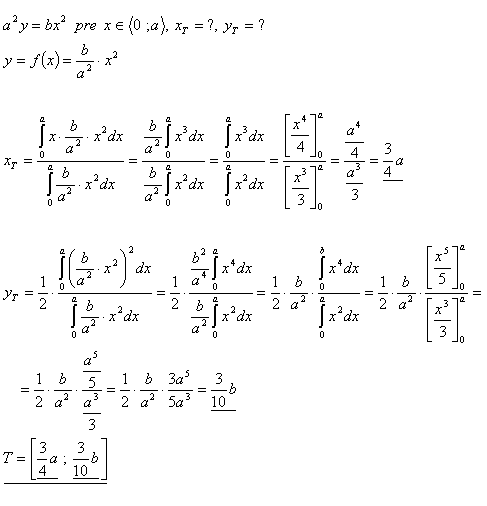Určitý integrál vo fyzike
1.Častica sa pohybuje priamočiaro so zrýchlením a = 2,6 m.s-2. Určite rovnicu rýchlosti a rovnicu dráhy (ak v0 = 0, s0 = 0). Vypočítajte rýchlosť a dráhu pohybu v čase t = 2s.
Riešenie:
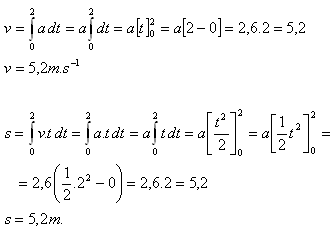
2.Určite prácu , ktorú musíme vykonať pri predĺžení pružiny o 25 cm z nenapnutého stavu, ak viete, že sila 16 N, rovnobežná s osou pružiny ju predĺži o 80 cm.
Riešenie:
F = 16 N, x = 80 cm = 0.8 m, a = 0, b = 25 cm = 0,25 m.
Sila F je priamo úmerná predĺženiu x
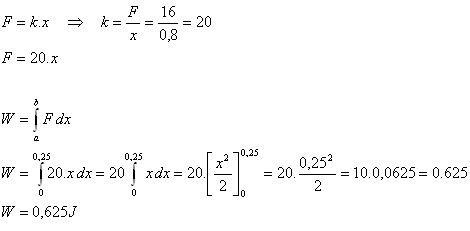
3.Určite efektívnu hodnotu striedavého sínusového prúdu
Riešenie:
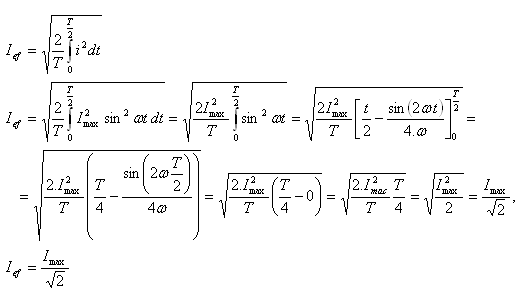
4.Špirálou variča s odporom R prechádza striedavý elektrický prúd s maximálnou hodnotou Imax. Odvoďte vzorec pre výpočet množstva Jouleovo tepla. Okamžitý prúd je: i = Imaxsin ωt.
Riešenie:
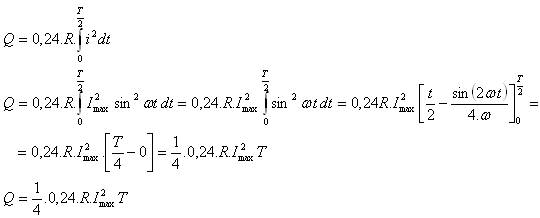
5.Akú dráhu prejde teleso, ktoré sa pohybuje rýchlosťou veľkosti v = At2 + Bt + C za prvých 10 sekúnd od začiatku pohybu, ak platí :
- A = 3ms-1
- B = 1ms-1
- C = –1ms-1
Riešenie:
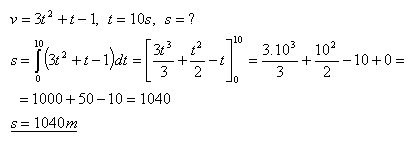
Teleso za 10 sekúnd prejde dráhu 1040 metrov.
6.Vypočítajte dráhu dažďovej kvapky za prvých 6 sekúnd. Odpor vzduchu zanedbajte.
Riešenie:
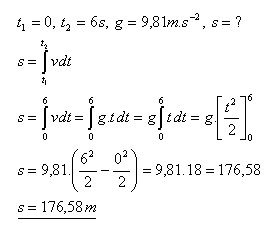
Kvapka vody za 6 sekúnd preletí 176,58m.
7. Akú prácu treba vykonať, aby teleso o hmotnosti m zväčšilo svoju rýchlosť z v1 na v2?
Riešenie:
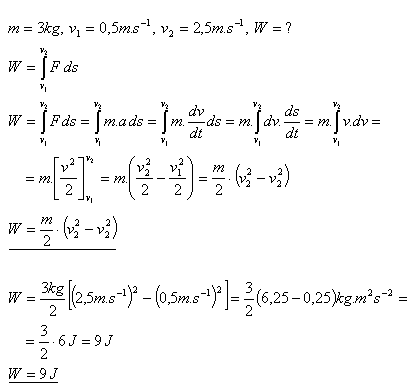
Pre zväčšenie rýchlosti telesa treba vykonať prácu W = 9J.
8.Akú prácu vykoná vonkajšia sila pri predĺžení oceľovej tyče z dĺžky l0 = 2m a obsahom prierezu
S = 5mm2 pružnou deformáciou o 1 mm?
Riešenie:
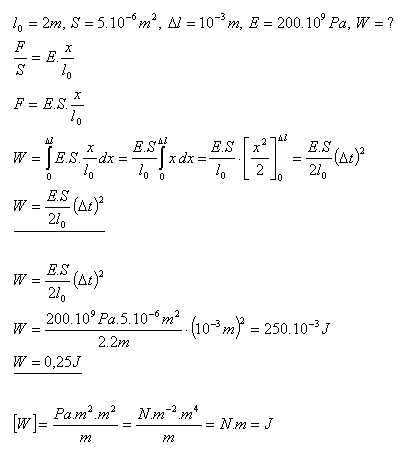
Vonkajšia sila pri predĺžení oceľovej tyče vykoná prácu W = 0,25J.
9.Vypočítajte prácu, ktorú treba vykonať pri zdvihnutí telesa o hmotnosti m do výšky h nad povrch Zeme. Použite vzťah:
Riešenie:
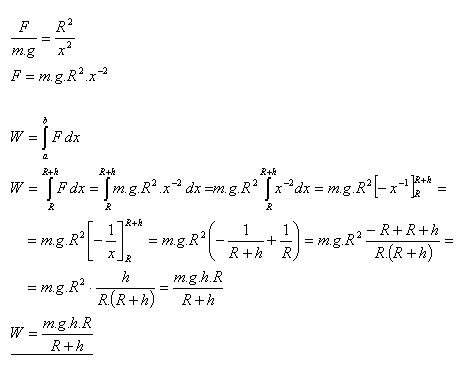
Práca potrebná na zdvihnutie telesa do výška h nad povrch Zeme je :
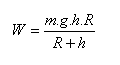
10. Za aký čas voda, naliata vo valcovej nádobe s obsahom dna S = 420cm2 a výškou vody h = 40cm vytečie cez otvor na dne. Otvor má obsah s = 2cm2. Pre výtokovú rýchlosť platí:
Riešenie:
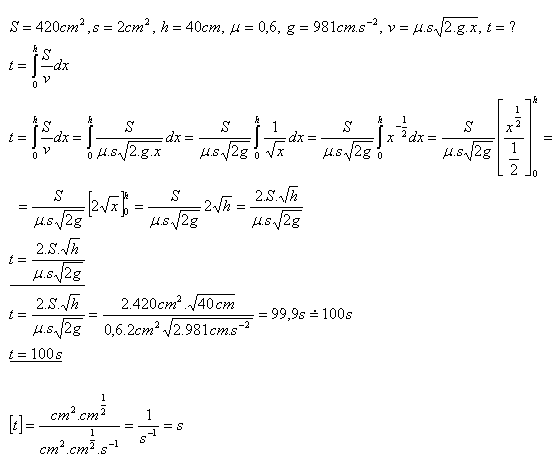
Voda vytečie za 100 sekúnd.
11.Vypočítajte súradnice ťažiska štvorca, ktorý má stranu a = 6 cm.
Riešenie:
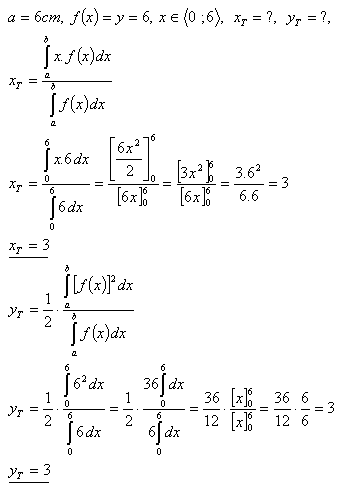
Ťažisko štvorca má súradnice T = [3 ; 3]
12.Vypočítajte súradnice ťažiska rovinného útvaru, ktorý je ohraničený funkciou:
- f(x) = y = x3, pre x e <0 ,1>
Riešenie:
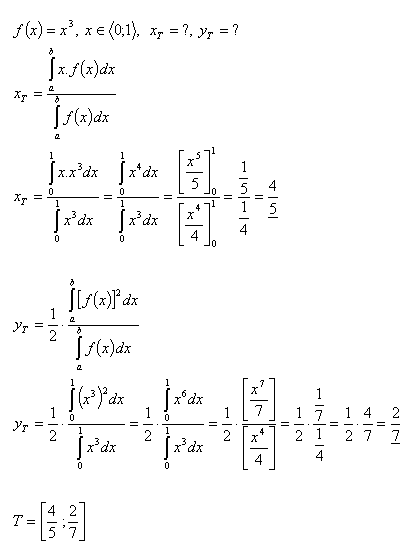
13. Vypočítajte súradnice ťažiska rovinného útvaru, ktorý je ohraničený:
- parabolou y = x2
- a priamkami y = 0, x = 1.
Riešenie:
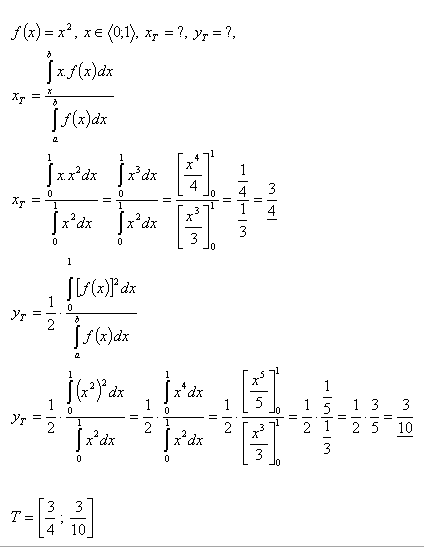
14.Určite súradnice trojuholníka ΔABO, ktorý vytvára
- priamka y = –x + 6 v súradnicovej sústave. A[6 , 0], B[0 ,6], O[0, 0]
Riešenie:
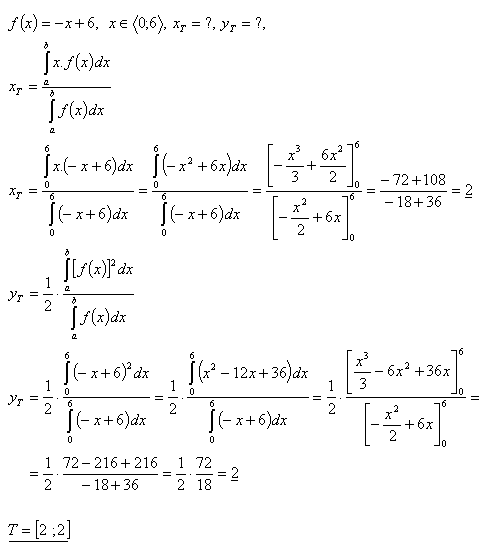
15. Zistite súradnice ťažiska rovinného útvaru, ktorý je ohraničený krivkou:
- a2y = bx2 pre x je z < 0 ; a >
Riešenie: