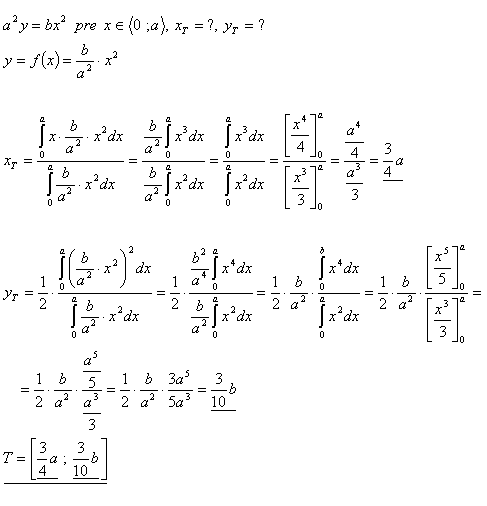Určitý integrál ve fyzice
1.Částice se pohybuje přímočaře se zrychlením a = 2,6 m.s-2. Určete rovnici rychlosti a rovnici dráhy (pokud v0 = 0, s0 = 0). Vypočtěte rychlost a dráhu pohybu v čase t = 2s.
Řešení:
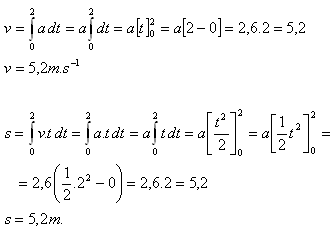
2.Určete práci, kterou musíme vykonat při prodloužení pružiny o 25 cm z nenapnutého stavu, pokud víte, že síla 16 N, rovnoběžná s osou pružiny ji prodlouží o 80 cm.
Řešení:
F = 16 N, x = 80 cm = 0.8 m, a = 0, b = 25 cm = 0,25 m.
Síla F je přímo úměrná prodloužení x
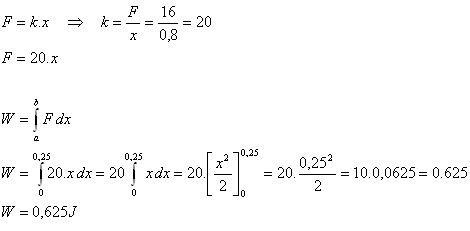
3.Určete efektivní hodnotu střídavého sinusového proudu
Řešení:
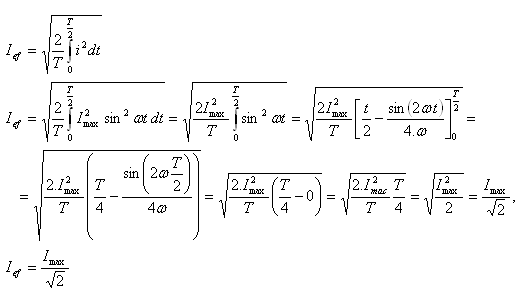
4.Spirálou vařiče s odporem R prochází střídavý elektrický proud s maximální hodnotou Imax. Odvoďte vzorec pro výpočet množství Jouleovo tepla. Okamžitý proud je i = Imaxsin ωt.
Řešení:
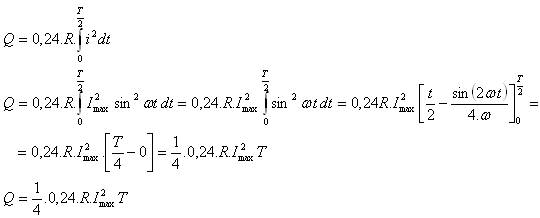
5.Jakou dráhu urazí těleso, které se pohybuje rychlostí velikosti v = AT2 + Bt + C za prvních 10 sekund od začátku pohybu, jestliže platí:
- A = 3ms-1
- B = 1ms-1
- C = –1ms-1
Řešení:
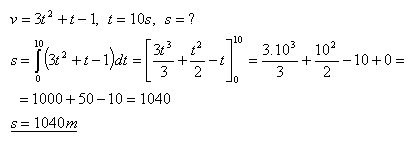
Těleso za 10 sekund přejde dráhu 1040 metrů.
6.Vypočítejte dráhu dešťové kapky za prvních 6 sekund. Odpor vzduchu zanedbejte.
Řešení:
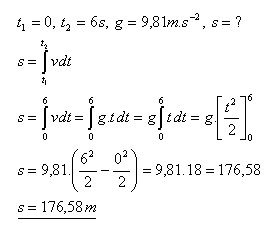
Kapka vody za 6 sekund proletí 176,58 m.
7. Jakou práci je třeba vykonat, aby těleso o hmotnosti m zvětšilo svou rychlost z v1 na v2?
Řešení:
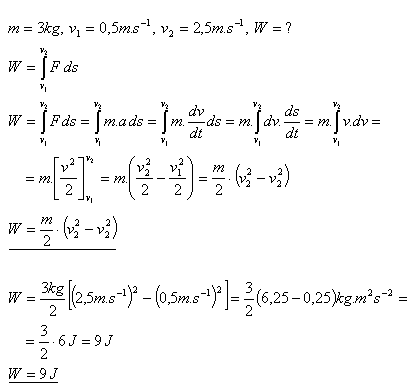
Pro zvětšení rychlosti tělesa třeba vykonat práci W = 9J.
8.Jakou práci vykoná vnější síla při prodloužení ocelové tyče z délky l0 = 2m a obsahem průřezuS = 5mm2 pružnou deformací o 1 mm?
Řešení:
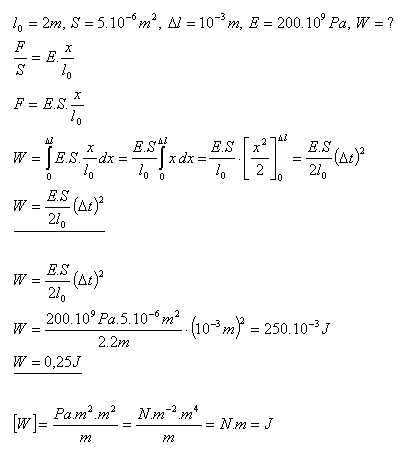
Vnější síla při prodloužení ocelové tyče vykoná práci W = 0,25 J.
9.Vypočítejte práci, kterou je třeba vykonat při zvednutí tělesa o hmotnosti m do výšky h nad povrch Země. Použijte vztah:
Řešení:
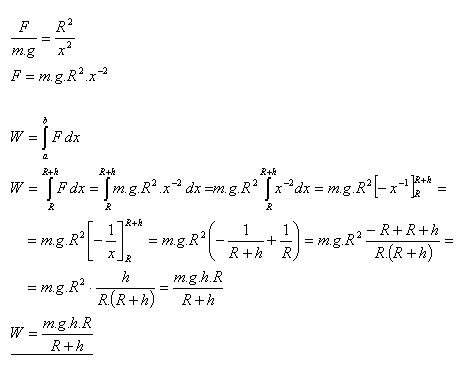
Práce potřebná pro zvednutí tělesa do výška h nad povrch Země je:
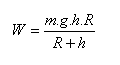
10. Za jaký čas voda, nalita ve válcové nádobě s obsahem dna S = 420cm2 a výškou vody h = 40cm vyteče přes otvor na dně. Otvor má obsah s = 2cm2. Pro výtokovou rychlost platí:
Řešení:
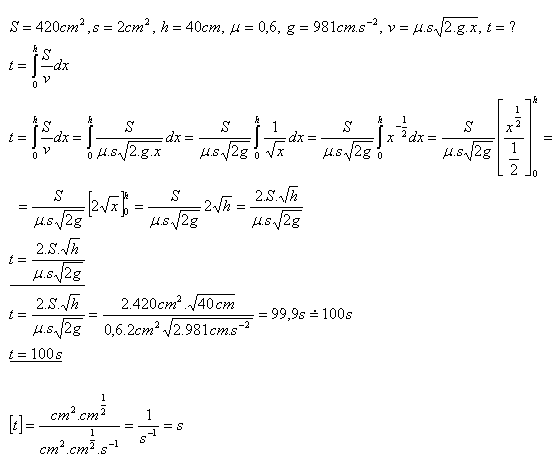
Voda vyteče za 100 sekund.
11.Vypočtěte souřadnice těžiště čtverce, který má stranu a = 6 cm.
Řešení:
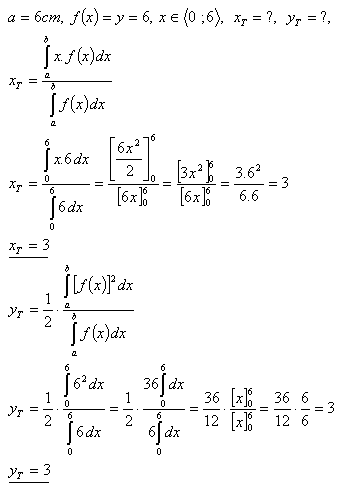
Těžiště čtverce má souřadnice T = [3 ; 3]
12.Vypočtěte souřadnice těžiště rovinného útvaru, který je ohraničen funkcí:
- f(x) = y = x3, pre x e <0 ,1>
Řešení:
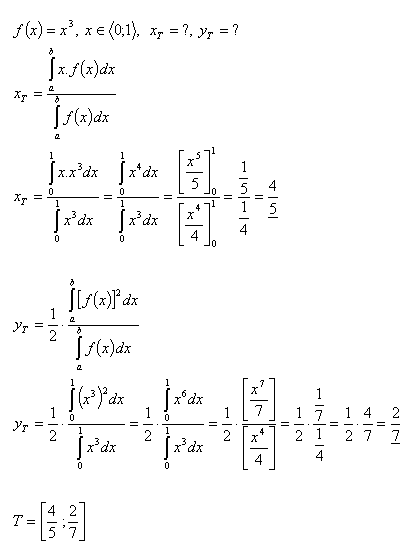
13. Vypočtěte souřadnice těžiště rovinného útvaru, který je ohraničen:
- parabolou y = x2
- a přímkami y = 0, x = 1.
Řešení:
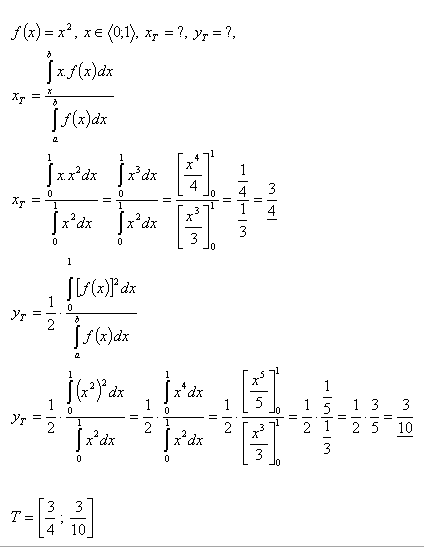
14.Určete souřadnice trojúhelníku ΔABO, který vytváří
- přímka y =-x + 6 v souřadnicové soustavě. A [6, 0], B [0, 6], O [0, 0]
Řešení:
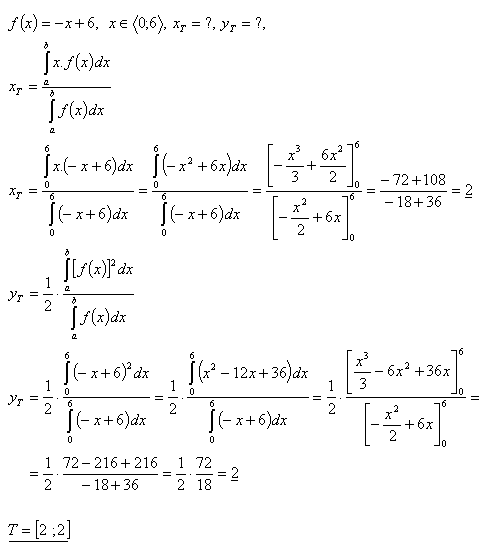
15. Zjistěte souřadnice těžiště rovinného útvaru, který je ohraničen křivkou:
- a2y = bx2 pre x je z < 0 ; a >
Řešení: