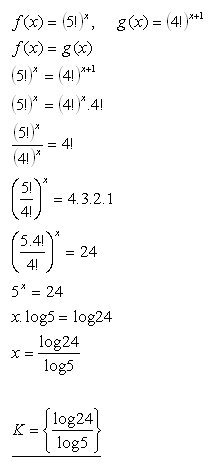Vlastnosti funkcí
1. Co si pamatujete o vlastnostech funkcí?
Řešení:
- Funkce f reálné proměnné x je předpis, který každému x e R přiřazuje nejvýše jedno y e R tak, že
y = f(x)
- Definiční obor funkce D je množina všech xe R, ke kterým existuje právě jedno ye R tak, že y = f (x).
- Obor hodnot funkce H je množina všech ye R, ke kterým existuje alespoň jedno xe R tak, že y = f (x).

Dvě funkce se rovnají : f(x) = g(x) pokud: D(f) = D(g)
f(x) = g(x)
Které z následujících grafů představují funkce?
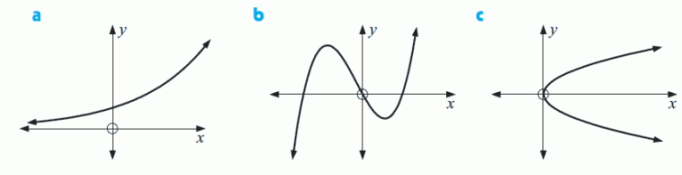
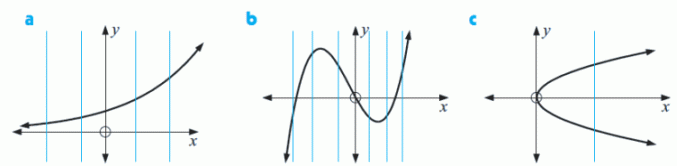
Funkce Funkce Není funkce
2.Zjistěte, zda následující výrazy jsou funkce:
Řešení:
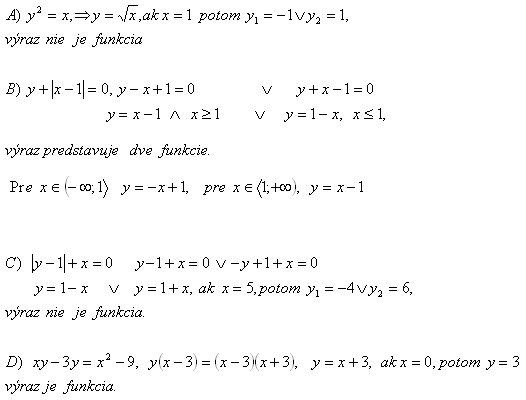
3.Rozhodněte, zda následující funkce se rovnají:
Řešení:
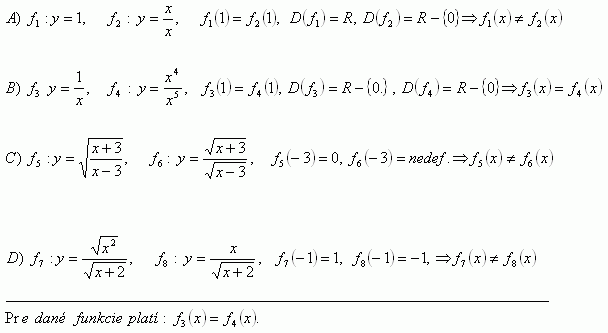
4.Rozhodněte o párnosti – sudost a nepárnosti – lichost funkcí:
Řešení:
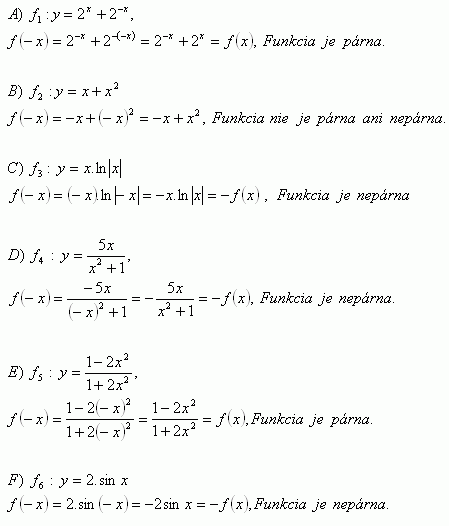
5. Zjistěte, které z následujících funkcí jsou ohraničené v daném definičním oboru.
Řešení:

6. K daným funkcím vytvořte inverzní funkce.
Řešení:
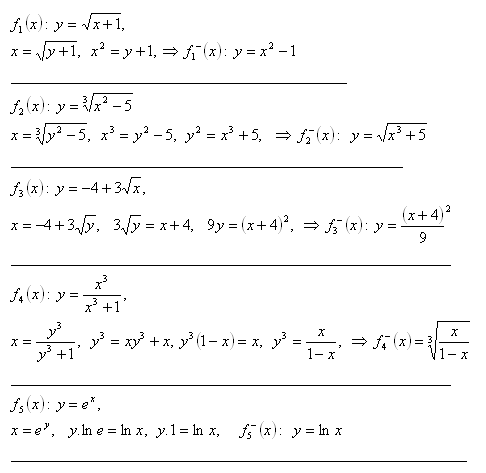
7. Určete inverzní funkci k funkcím:
Řešení:
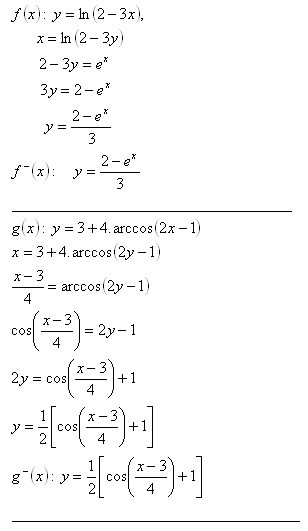
8.Ve funkci f(x) : y = ax2 +bx +c , x e R, urč a,b,c e R tak aby platilo f(0) = -3, f(-1) = -6, f(2) = 15.
Řešení:
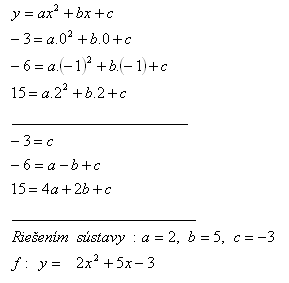
9. Určete b , d funkcie f: y = ( x +b ):( x +d) tak, aby platilo f(1) = -1, f(-1) = -1/3
Řešení:
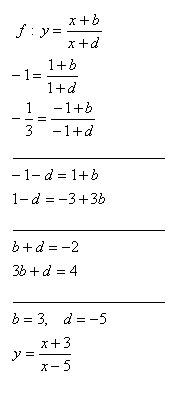
10. Určete množinu všech funkcí f(x), pro které platí:
Řešení:

11.Daná je funkce f: y= -2x +3
a.) Určete f(0), f(-5)
b.) Pro které x platí f(x) = 1, f(x) =-5
c.) Určete průsečík grafu funkce se souřadnicovými osami
Řešení:
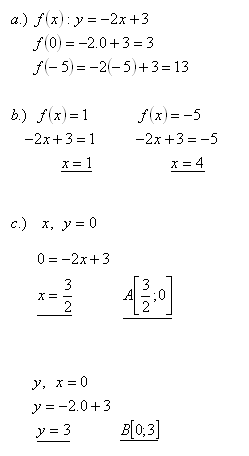
12.Napište lineární funkci, jejíž graf prochází body:
Řešení:
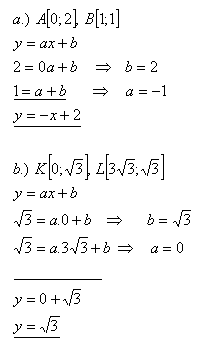
Rovnice funkcí jsou: f1: y = – x + 2 a f2: y = √3.
13.Podle výrobce automobilu je spotřeba benzínu auta na 100 km. následující. Při rychlosti 80 km.h-1 6 litrů benzínu, při rychlosti 110 km.h-1 8,1 litru. Určete spotřebu auta při rychlosti 90 km.h-1.
Řešení:
x = rychlost, y = spotřeba
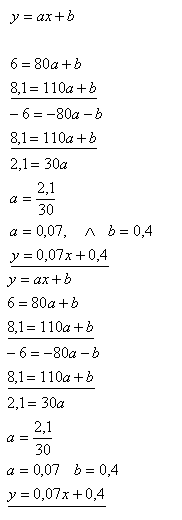
Spotřeba pri rychlosti 90 km.h-1.
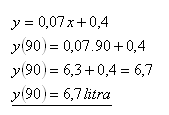
Spotřeba automobilu při rychlosti 90 km.h-1 je 6,7 litru benzínu na 100 kilometrů.
14.Daná je funkce f: y = x2 - 4x -12.
a.) Učete pro které x platí f(x) = 9
b.) Učete průsečíky grafu funkce se souřadnicovými osami
Řešení:
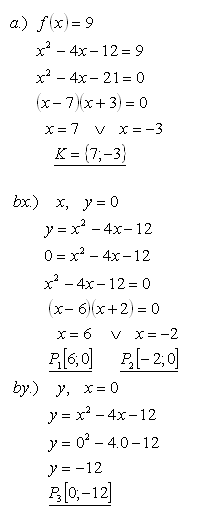
15.Napište kvadratickou funkci, jejíž prvky jsou uspořádány dvojice
A[0;1], B[2;-1], C[1;-1]
Řešení:
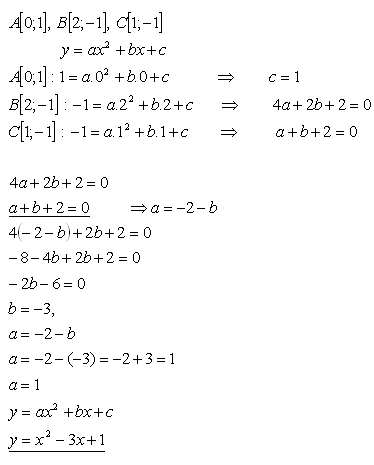
Kvadratická funkce má rovnici: f : y = x2 - 3x +1
16.Daná je kvadratická funkce f: y = x2 – 3x + c. Určete c tak, aby funkce:
a). neměla společný bod s osou x
b.) měla právě jeden společný bod s osou x
c.) měla právě dva společné body s osou x
Řešení:
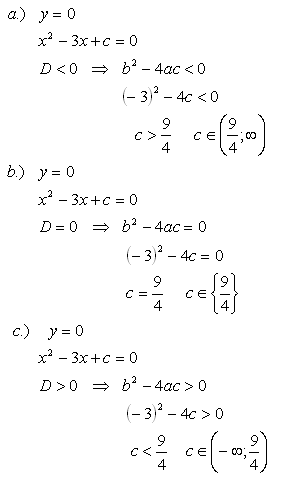
17.Daná je kvadratická funkce f: y = x2 + 4x – 5. Určete její průsečíky se souřadnicovými osami a vrchol její parabolického grafu.
Řešení:
S osou x: y = 0 S osou y : x = 0

18.Určete koeficienty a, b tak, aby graf funkce f: y = a.log x + b procházel body K, L pokud platí:
Řešení:
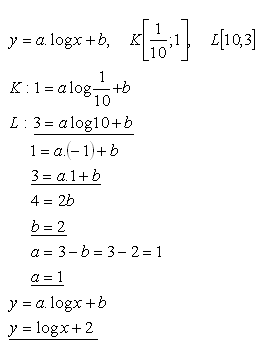
Rovnice logaritmické funkce má tvar: y = log x +2.
19.Určete koeficienty a, b tak, aby funkce f: y = a2x + b procházela počátkem souřadnicové soustavy a bodem M [1; 1].
Řešení:
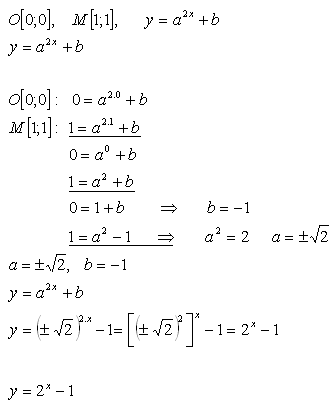
Funkce má tvar f: y = 2x - 1.
20.Pro která reálná čísla x nabývají funkce f(x) = (5!)x a funkce g(x) = (4!)x+1 rovnaké hodnoty?
Řešení: