Extrémy - slovní úlohy
1.Číslo 32 rozložte na dvou sčítanců tak, aby jejich součin byl největší.
Řešení:
První sčítanec : x x = 16
Druhý sčítanec : 32 – x 32 – 16=16
y = x.(32 – x)
y = 32x – x2
y‘ = 32 – 2x
32 – 2x = 0
2x = 32
x =16
y‘‘ = -2 < 0 - maximum
První sčítanec je 16, druhý také 16
2.
Číslo 16 rozložte na dvou sčítanců tak, aby součet druhých mocnin těchto sčítanců byl nejmenší.
Řešení:
První sčítanec : x x = 8
Druhý sčítanec : 16 – x 16 – 8 = 8
y = x2 + ( 16 – x )2
y = x2 + 256 -32x +x2
y = 2x2 – 32x + 256
y‘ = 4x – 32
4x - 32 = 0
4x = 32
x = 8
y‘‘ = 4 > 0 - minimum
První sčítanec je 8, druhý také 8
3.Najděte takové kladné číslo x, aby součet tohoto čísla a jeho převrácené hodnoty byl nejmenší.
Řešení:
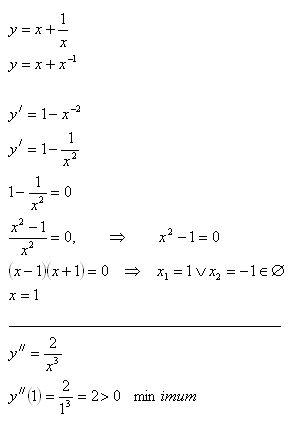
Hledané číslo je x = 1.
4.Z drátu délky l = 120 cm máme udělat model kvádru se čtvercovou podstavou. Jaké má mít rozměry, aby povrch byl maximální?
Řešení:
Hrana čtvercové podstavy : a = b =x
Výška kvádru: c
8x + 4c = l
8x +4c =120/:4
2x + c = 30
c = 30 – 2x
S = 2( ab + ac + bc )
S = 2( x.x + x(30 – 2x) + x(30 – 2x))
S = 2(-3x2 +60x )
S = -6x2 +120x
S‘ = -12x + 120 S‘‘ = -12 < 0 maximum
-12x + 120 = 0
12x = 120
x = 10
c = 30 -2x = 30 – 2.10 = 10
x = 10 cm, c = 10 cm .
Kvádr musí mít tvar krychle s hranou x = 10 cm
5. Zahrada tvaru obdélníku má obvod 200 m. Určitě rozměry zahrady tak, aby její obsah byl maximální.
Řešení:
a = x
O = 2a + 2b
200 = 2x +2b/:2
100 = x + b
b = 100 – x b = 100 – x = 100 – 50 = 50
b = 50 m
S = a.b
S = x.(100 – x )
S = 100x – x2
S‘ =100 – 2x S‘‘ = -2 < 0 - maximum
100 – 2x = 0
2x = 100
x = 50
a = 50 m
Zahrada bude mít maximální obsah bude-li tvaru čtverce o straně a = b = 50 m..
6.Kdy má kvádr o objemu V = 63 cm3 a výškou v = 7 cm nejmenší povrch?
Řešení:
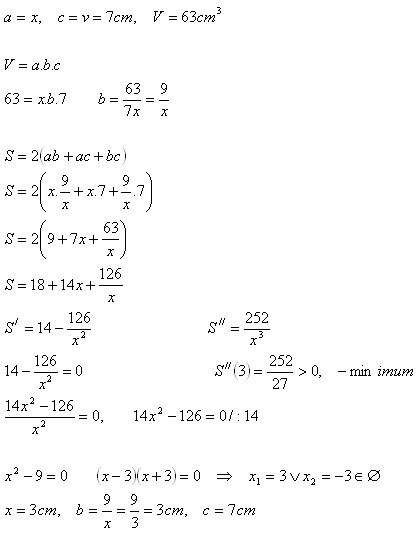
Rozměry hledaného kvádru jsou a = 3 cm, b = 3 cm, c = 7 cm
7.
Na břehu řeky třeba oplotit zahradu obdélníkového tvaru (jednu stranu obdélníku tvoří řeka) pletivem dlouhým l = 800 m. Jaké rozměry musí mít zahrada, aby jí výměra byla maximální?
Řešení:
800 = 2a +b
a = x
b = 800 – 2a = 800 – 2x
S = a.b
S = x.(800 – 2x)
S = 800x – 2x2
S‘ =800 – 4x S‘‘ = -4 < 0 - maximum
800 – 4x = 0
4x = 800
x = 200
x = 200 m
b = 800 – 2x
b = 800 – 400 = 400
b = 400 m
Rozměry zahrady jsou a = 200 m, b = 400 m.
8.Jaké jsou rozměry otevřeného bazénu se čtvercovým dnem, pokud bazén má objem V = 32 m3 a pokud na jeho vyzdění má spotřebovat minimální množství materiálu.
Řešení:
V = 32 m3, x – hrana čtvercové podstavy, v - výška kvádru
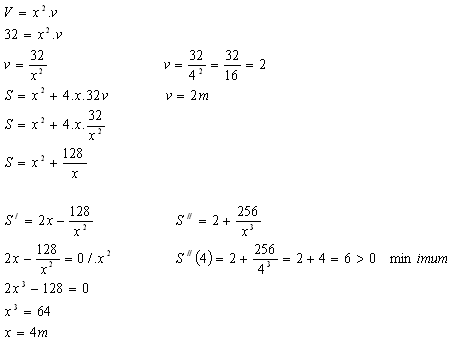
Rozměry: a=4m, b=4m, v=2m
9. Drát s délkou 5 m ohněte do pravého úhlu tak, aby vzdálenost obou konců byla minimální. Kde je třeba drát ohnout?
Řešení:
Odvesny a = x, b = 5 – x
Přepona c = y
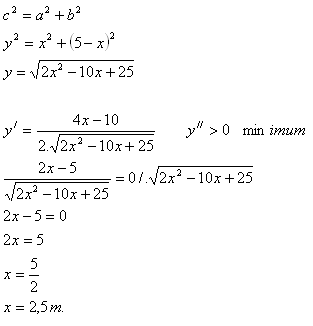
Drát třeba ohnout v prostředku.
10. Z plechu tvaru čtverce o straně 30 cm třeba v rozích vystřihnout čtyři stejné čtverečky, zbytek přehnout tak, aby vznikla otevřená krabice. Určitě stranu odstřižených čtverečků x tak, aby objem krabice byl maximální.
Řešení:
a = 30 – 2x, b = 30 – 2x, c = x
V = a.b.c
V = (30 – 2x)(30 – 2x).x
V = 4x3 – 120x2 +900x
V‘ = 12x2 – 240x +900 V‘‘ = 24x -240
12x2 – 240x +900 =0 /:12 V‘‘(5) = 24.5-240 = -120 < 0 maximum
x2 - 20x + 75 = 0
( x – 5 )( x -15 ) = 0 x1 = 5 x2 = 15 -nevyhovuje
x = 5 cm
Strana ustřiženého čtverečku je x = 5 cm.
11.Jáma s objemem 500 m3 má tvar kvádru se čtvercovou podstavou se stranou xa hloubkou h. Při jakých rozměrech x a h bude mít jáma minimální povrch?
Řešení:
Rozbor:
V = 500 m3, x = ?, h = ?
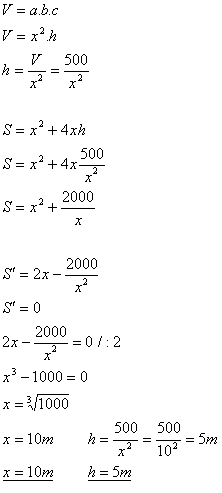
Jáma má podstavu čtverec o straně x = 10m a výšku h = 5m.
12.Daná je parabola y = 4 - x2. Najděte vrcholy obdélníku ABCD s největším obvodem, jehož vrcholy A, B leží na ose x, vrcholy C, D mají kladné y-ové souřadnice a leží na parabole.
Řešení:
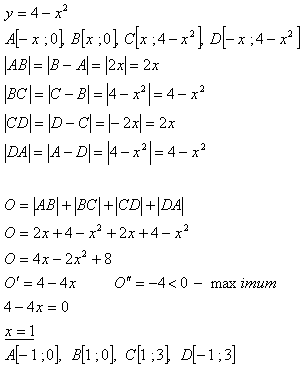
Body jsou: A[-1;0], B[1;0], C[1;3], D[-1;3]
13.Určete rozměry (r, v) válcové nádoby bez víka, jejíž povrch je S = 27π tak, aby její objem byl největší.
Řešení:
Rozbor:
S = 27π, r = x
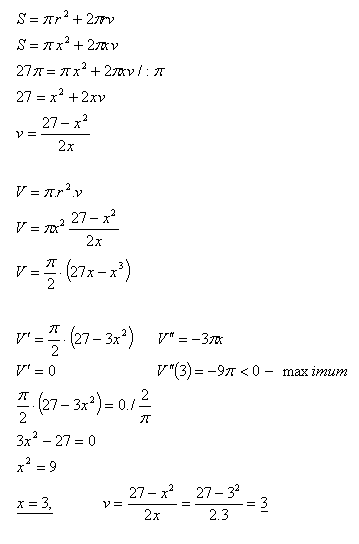
Rozměry nádoby jsou r = x = 3j, v = 3j.
14.Nahoru otevřená nádoba tvaru válce má objem V = 3140 cm3. Určete rozměry válce (r, v) tak, aby na vytvoření této nádoby se minulo nejméně materiálu.
Řešení:
Rozbor:
V = 3140 cm3, r = x = ?
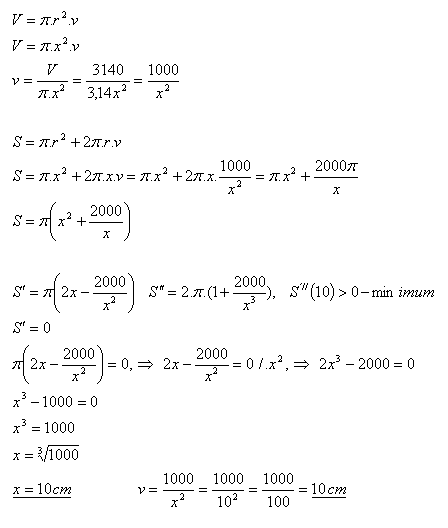
Rozměry nádoby jsou r = x = 10cm, v = 10cm.
15. Jaké rozměry musí mít obdélník s obvodem O = 40cm, aby jeho úhlopříčka byla minimální.
Řešení:
Rozbor:
x = a = ?, b = ?
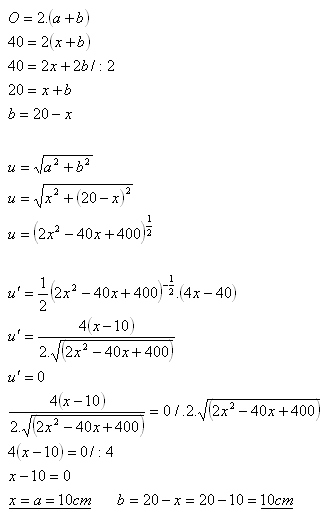
Útvar je čtverec o straně a = 10cm.