Pohyby v radiálním gravitačním poli
1. Charakterizujte radiální gravitační pole Země.
Řešení:
Pokud trajektorie hmotného bodu při pohybu v gravitačním poli Země je srovnatelná s rozměry Země, gravitační pole je radiální. Radiální gravitační pole je prostorově neohraničené. Na různých místech takového pole má gravitační zrychlení různý směr, neboť stále směřuje do středu Země a rozličnou velikost, která závisí na vzdálenosti daného místa od středu Země. Příkladem pohybu v radiální gravitační pole Země jsou pohyby umělých družic Země, pohyby mezikontinentálních střel a raket atd…
Na těleso o hmotnosti m působí při pohybu v gravitačním poli Země:
a ) dostředivá síla:
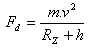
b) gravitační síla:
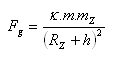
Těleso má:
a) kinetickou energii:
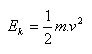
b) potenciálnu energiu:
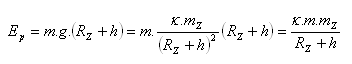
Pro radiální gravitační pole Slunce platí tři Keplerovy zákony :
1. ) Planety se pohybují kolem Slunce po elipsách málo odlišných od kružnic, ve společném ohnisku je Slunce.
2. ) Plochy opsané průvodičem planety za stejný čas jsou stejné.
3.) 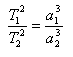 T1, T2 jsou oběžné doby dvou planet, a1, a2 jsou hlavní poloosy jejich trajektorií .
T1, T2 jsou oběžné doby dvou planet, a1, a2 jsou hlavní poloosy jejich trajektorií .
2.Vypočtěte první a druhou kosmickou rychlost.
Řešení:
- a.) První kosmická rychlost v1
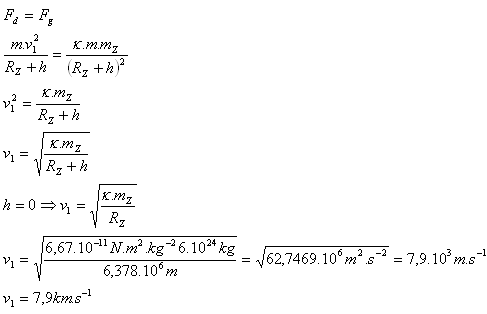
- b.) Druhá kosmická rychlost v2
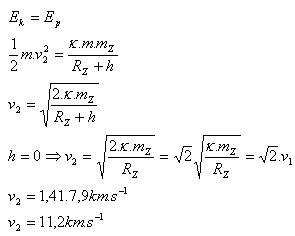
- První kosmická rychlost (kruhová) je v1 =7,9 km.s-1.
- Druhá kosmická rychlost (parabolická, úniková) je v2 = 11,2 km.s-1. Těleso se trvale vzdaluje od Země ale zůstává v gravitačním poli Slunce.
- Třetí kosmická rychlost je v3 = 16,7 km.s-1. Těleso opouští gravitační pole Slunce.
3. V jisté době byly ze Země pozorovány dvě družice v různých výškách (h1 = RZ, h2 = 2RZ), které se pohybovaly po kruhových trajektoriích stejným směrem. Určete jejich rychlosti. v1 = 7,9 km.s-1
Řešení:
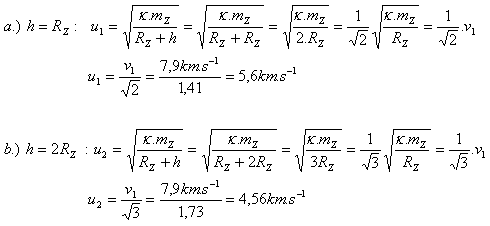
Rychlosti družic jsou u1 = 5,6 km.s-1 a u2 = 4,56 km.s-1.
4.Určete parabolickou (druhou kosmickou) rychlost na povrchu Měsíce. mM=7,41.1022 kg, RM=1,736.106 m
Řešení:
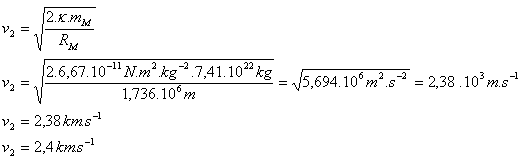
Druhá kosmická rychlost (parabolická, úniková) na povrchu Mesiaca je v2 = 2,4 km.s-1
5. Hmotnost Slunce je mS = 1,989 1030 kg. Rychlost oběhu Země kolem Slunce je v = 29,82 km.s-1. V jaké vzdálenosti obíhá Země kolem Slunce?
Řešení:
Rozbor:
mS =1,989 1030 kg, v = 29,82 km.s-1= 29,82.103 m.s-1
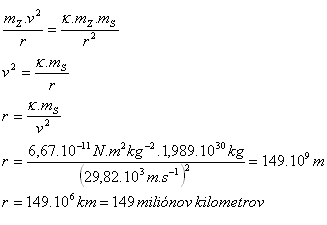
r (přesne) = 149 597 900 km
Lze použít zaokrouhlená hodnota AU = 150.106 km. Je to „astronomická jednotka“.
6.Měsíc obíhá kolem Země ve vzdálenosti 384 000 km a má hmotnost 7,41.1022 kg. Na spojnici středů obou těles najděte bod C, ve kterém by byl člověk ve stavu beztíže. V tomto bodě se gravitační síla Země rovna gravitační síle Měsíce.
7.Největší planeta Sluneční soustavy Jupiter obíhá kolem Slunce ve vzdálenosti 7,8.108 km. Hmotnost Slunce je 1,989.1030 kg. Jakou hmotnost má Jupiter, pokud ho Slunce přitahuje gravitační silou Fg = 4,2.1023 N? Jak velké zrychlení uděluje Slunce Jupiteru? Jaký je oběžný čas (perioda T) Jupitera kolem Slunce?
Řešení:

Hmotnost Jupitera je 1,9.1027 kg, jeho zrychlení 2,2.10-4 ms-2. Oběžná doba Jupitera kolem Slunce je 11,8 let (pozemských)
8.V jaké výšce h nad Zemí se musí umístit stacionálna družice, která se nachází nad stejným místem nad povrchem Země?
Řešení:
Rozbor:
mZ = 6.1024 kg, RZ = 6,378.106m, TZ = 23hod. 56min. 4sek = 8,6164.104s
mD = hmotnost družice
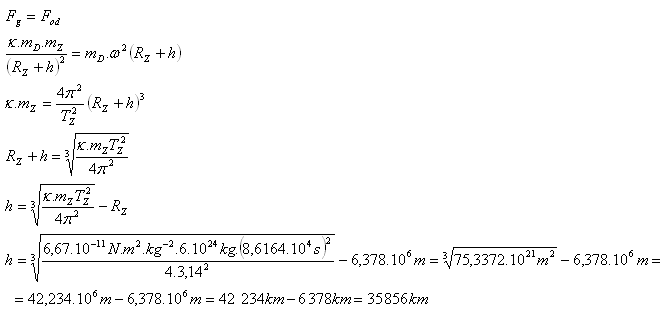
Stacionární družici třeba umístit do výšky 35 856 km nad Zemí.
9. Pomocí Keplerových zákonů zjistěte:
- a.) Jaká je střední vzdálenost planety Venuše od Slunce, pokud její doba oběhu kolem Slunce je TV=0,615 roka.
- b.) Jaké je doba oběhu planety Merkur kolem Slunce, pokud její střední vzdálenost od Slunce je
aM = 0,387AU
Řešení:

- Vzdálenost Venuše od Slunce je asi 108,5.106 km.
- Oběžná doba Merkuru kolem Slunce je asi 88 dní.
10.Kosmická loď startuje ze stacionární oběžné stanice umístěné ve výšce h = 35 856 km nad Zemí (viz přík. Č.8) směrem na Měsíc. Za jaký čas se kosmická loď dostane do oblasti Měsíce?
Řešení:
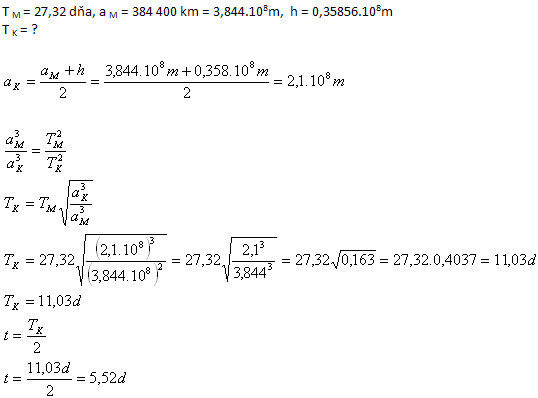
Čas 11,03 dne je perioda celé dráhy kosmické lodi. Cesta ze Země na Měsíc trvá polovinu této periody, čili asi 5,52 dne.