Jehlan a kužel
1. Charakterizujte výpočet objemu a obsahu pre:
- jehlan
- komolý jehlan
- kužel
- komolý kužel
Řešení:

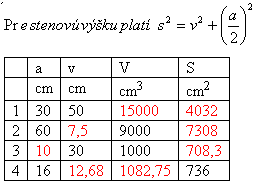
2. Je dán pravidelný čtyřboký jehlan (podstava je čtverec o straně a).
Doplňte chybějící hodnoty tabulky.
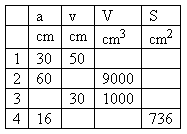
Řešení:
3. Nad každou stěnou krychle s hranou a = 30 cm je sestrojen pravidelný čtyřboký jehlan s výškou 15 cm.
Vypočítejte objem takto vzniklého tělesa, pokud vrcholy jehlan:
a) leží mimo kostky
b) leží uvnitř kostky
Řešení:
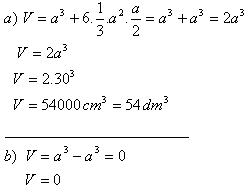
Objem tělesa v prvním případě je V = 54 dm
3, v druhém případě je nulový.
4. Vypočítejte objem jehlanu, jehož boční hrana délky 5 cm zvíře se čtvercovou podstavou úhel α = 60°. (Úhel α je úhel mezi hranou a úhlopříčkou podstavy.)
Řešení:
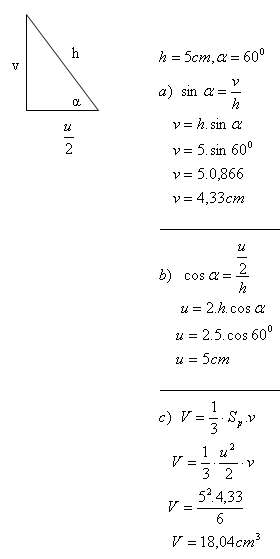
Objem jehlanuje V = 18,04 cm
3.
5. Určete hmotnost betonového pilíře (ρ = 2,2 g.cm-3) tvaru pravidelného čtyřbokého komolého jehlanu, jestliže jeho čtvercové postavy mají strany a = 45 cm, b = 25cm a výška pilíře je v = 33 cm.
Řešení:
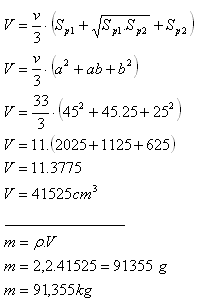
Hmotnost betonového pilíře je m = 91,355 kg.
6. Daný je kužel s rozměry uvedenými v tabulce.
Doplňte tabulku.

Řešení:
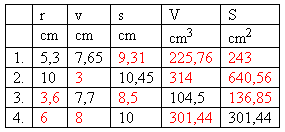
7. Pravoúhlý trojúhelník s odvěsnami a = 3 cm, b = 4 cm rotuje kolem delší odvěsny.
Vypočítejte objem a povrch takto vzniklého kužele.
Řešení:
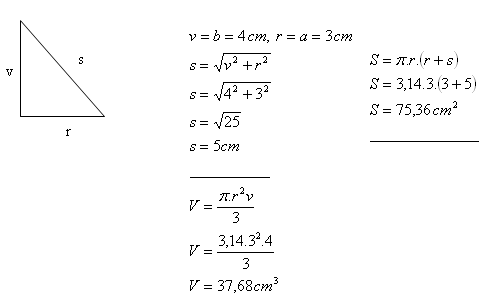
Kužeľ má objem V = 37,68 cm
3 a povrch S = 75,36 cm
2.
8. Povrch kužele je S = 235,5 cm2. Osový řez kuželem je rovnostranný trojúhelník.
Vypočítejte objem kužele.
Řešení:
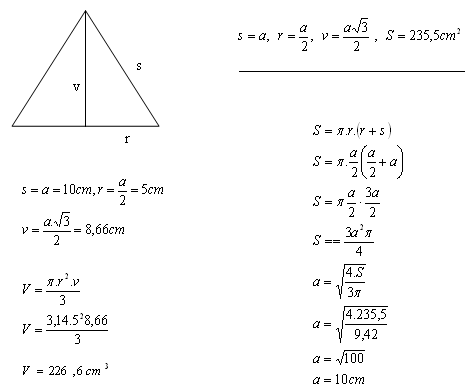
Objem kužeľa je 226,6 cm
3.
9. Plášť kužele rozvinutý do roviny má tvar kruhového výseku se středovým úhlem α = 150° a obsahom S = 523,4 cm2.
Vypočítejte rozměry tohoto kužele a jeho objem.
Řešení:
S = 523,4cm
2 - obsah kruhového výseku s poloměrem R - obsah pláště s poloměrem r
o = R. arcα - kružnicových oblouk odpovídající výseku
O = 2π.r - délka podstavovej kružnice kužele
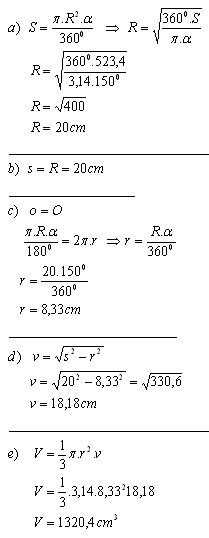
Rozměry kužele jsou r = 8,33 cm, s = 20 cm, v = 18,18 cm a objem V = 1320,4 cm
3.
10. Povrch komolého kužele je 7693 cm2, polomery podstáv sú 28 cm a 21 cm.
Vypočítejte výšku kužele a jeho objem.
Řešení:
S = 7693 cm
2
R = 28 cm
r = 21 cm
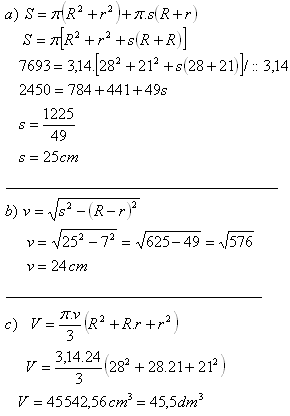
Výška kužele je v = 24 cm, jeho objem V = 45,5 dm
3.
11. Objem komolého kužele je V = 38 000π cm3. Poloměr dolní podstavy je o 10 cm větší, než poloměr horní podstavy.
Určete poloměr podstavy, pokud v = 60 cm.
Řešení:
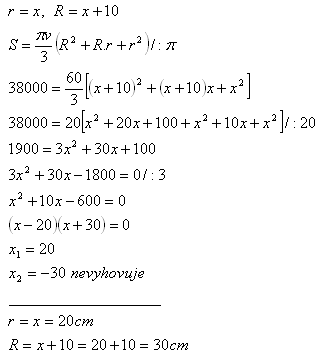
Polomery podstáv zrezaného kužeľa sú R = 30 cm a r = 20 cm.
12. Komolý kužel s poloměry x = 15 cm, y = 13 cm a výškou v = 9 cm rozvalcovali na válec o poloměru r = 7,67 cm.
Jaká je délka tohoto válce?
Řešení:
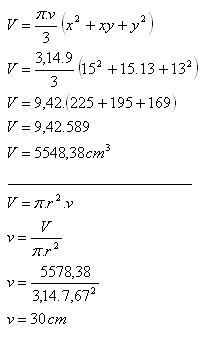
Délka / výška válce je 30 cm.