Binomická věta
1. Napíše binomickou větu a její vlastnosti:
Binomická věta a Pascalov trojúhelník.
2. Zjednodušte:
Řešení:
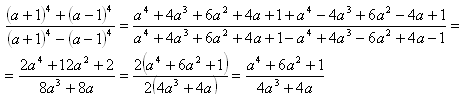
3. Zjednodušte:
Řešení:
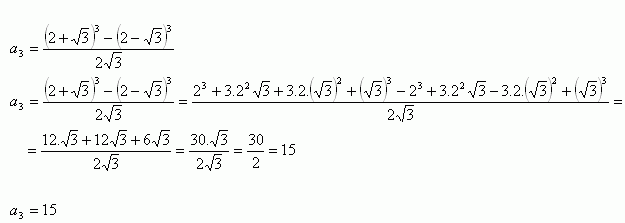
4. Určete čttvrtý člen binomického rozvoje:
Řešení:
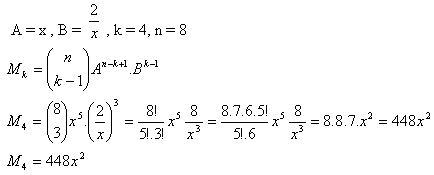
5. Určete člen binomického rozvoje ( x + x-1)8, který neobsahuje x.
Řešení:
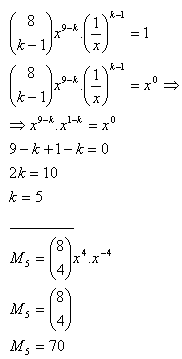
Je to člen M
5 = 70.
6. Který člen rozvoje (2x3 + x–1)10 obsahuje x6.
Řešení:
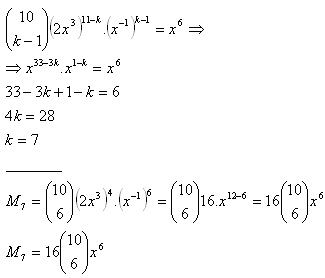
7. V rozvoji (a + 2a3)n je koeficient 3. člena o 44 větší než koeficient 2. člena.
Určitě, pro které přirozené číslo platí uvedené podmínky.
Řešení:
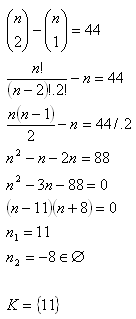
8. Pro které x se v rozvoji výrazu rovná M5 = 105?
Řešení:
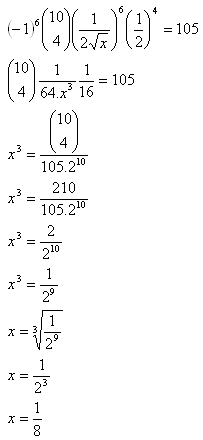
9.Zjistěte který člen daného rozvoje obsahuje x7, pokud platí:
Řešení:
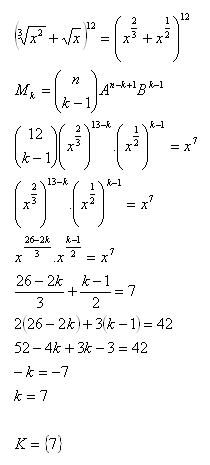
Hodnotu x7 obsahuje siedmy člen rozvoja.
10.Najděte největší koeficient binominálního rozvoje (a + b)n, kdy součet všech koeficientů je 4096.
Řešení:
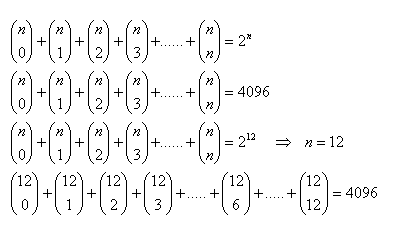
Největší koeficient binominálního rozvoje je prostřední koeficient
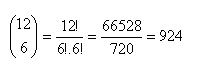
Největší koeficient binominálního rozvoje je 924