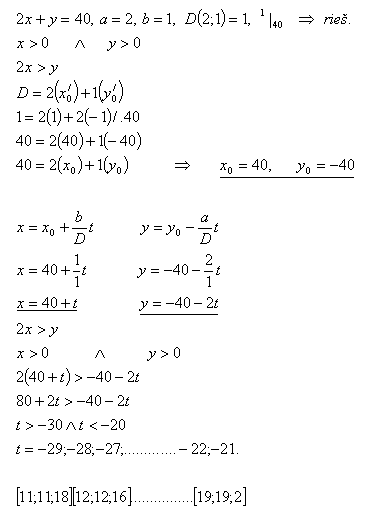Diofantické rovnice
1. Řešte rovnice:
ax + by = 0 a ax + by = c
Řešení:
Řecký matematik DIOFANTOS (asi 250 r. před nl) se zabýval řešením rovnic typu ax + by = c, přičemž za řešení připouštěl jen celá čísla. Takové rovnice nazýváme „diofantické rovnice“
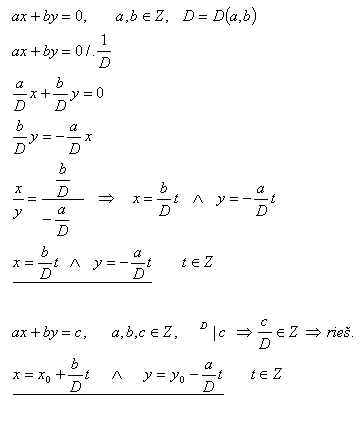
2.V množině Z řešte rovnici:
6x – 4y = 0
Řešení:
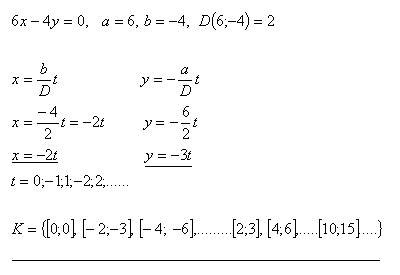
3.V množině Z řešte rovnici:
3x + 15y = 0
Řešení:
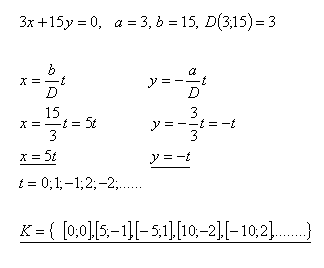
4.Zjistěte, které z následujících rovnic jsou řešitelné v množině Z:
Řešení:
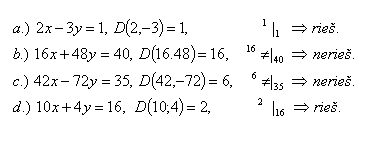
5.V množině Z řešte rovnici:
10x + 4y = 16
Riešenie:
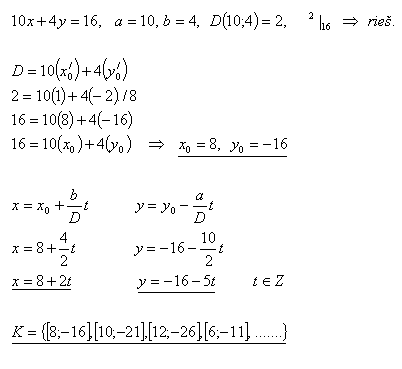
6.V množině Z řešte rovnici:
21x +15y = 3
Řešení:
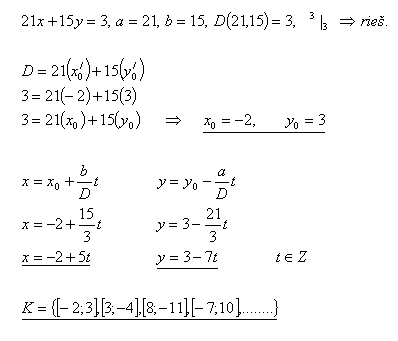
7.Jaké rozměry (v celých číslech) může mít obdélník, ktoréhoobvod je 24 cm?
Řešení:
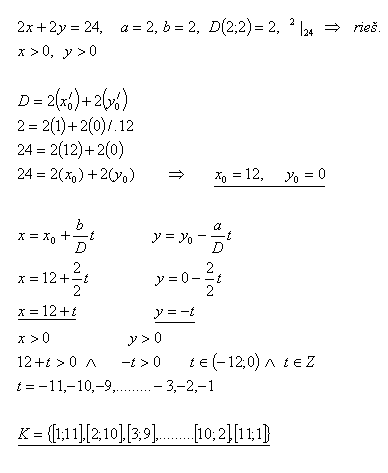
8.Jakým způsobem je možné zaplatit částku 21 Eur, pokud máme k dispozici pouze dvou - a pětieurovky?
Řešení:
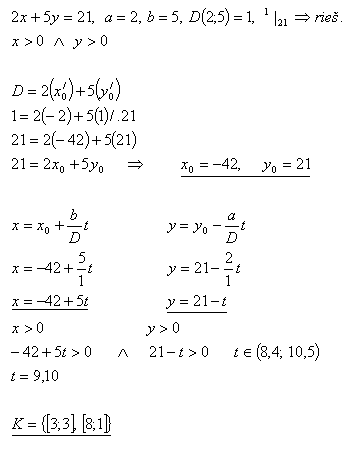
9.Zjistěte kolika způsoby lze 22 litrů vína přelít do dvoulitrových a třílitrových nádob.
Řešení:
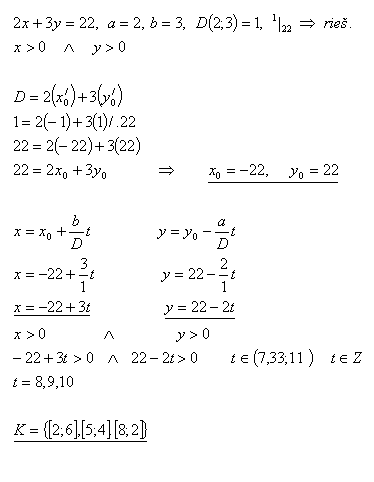
10.Stužku dlouhou 50cm chceme nastříhat na části 6cm a 4cm dlouhé. Kolika způsoby to můžeme udělat?
Řešení:
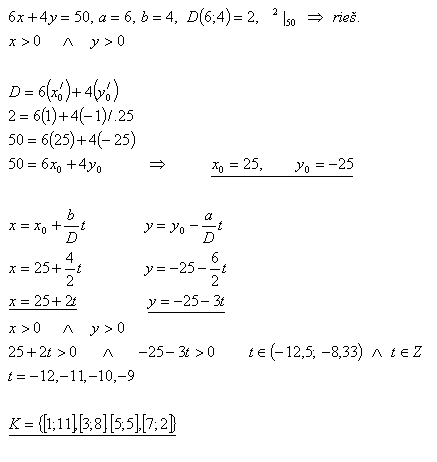
11.Určitě všechny rovnoramenné trojúhelníky, jejichž strany jsou celá čísla a obvod se rovná 40 cm.
Řešení: