Interference světla
1.Vysvětlete podstatu a způsoby interference světla.
Řešení:
Interference vzniká skládáním dvou světelných vln, které musí být koherentní. Musí mít stejné frekvence a stálý fázový rozdíl. Podmínku koherence nemohou splnit světelné vlny ze dvou různých
zdrojů. Může se toho dosáhnout rozdělením světelné vlny z jednoho zdroje na dvě koherentní vlny. Dá se toho dosáhnout:
- a) odrazem vlny od překážky – interference odrazem
- b) ohybem vlny za překážkou nebo za štěrbinou – interference ohybem
Interferenční maximum – místo, kde se světlo interferencí zesiluje
Interferenční minimum – místo, kde se světlo interferencí zeslabuje nebo ruší.
Interferenční maxima a minima:
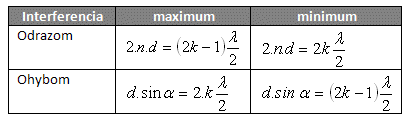
k = 1,2,3,....
2.Určete tloušťku stěny mýdlové bubliny (n = 1,33), na kterou dopadá bílé světlo. Interferenční maximum prvního řádu pozorujeme v zelené barvě (fZ = 5,7·1014Hz).
Řešení:
Rozbor:
n = 1,33, fZ = 5,7·1014Hz, c = 3·108m·s-1, d = ? k = 1
Jde o použití vztahu pro interferenční maximum prvního řádu odrazem.
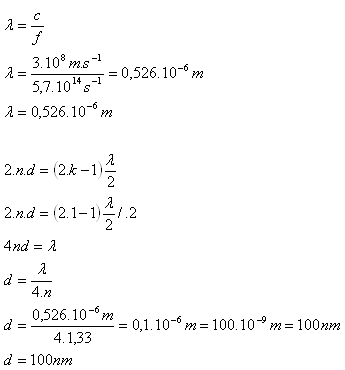
Tloušťka stěny mýdlové bubliny je d = 100 nm.
3.Tloušťka olejové skvrny je d = 2,4·10-7m a index lomu oleje je n = 1,5. Které barvy odraženého světla se interferencí zruší?
Řešení:
Rozbor:
Jde o interferenční minimum odrazem.
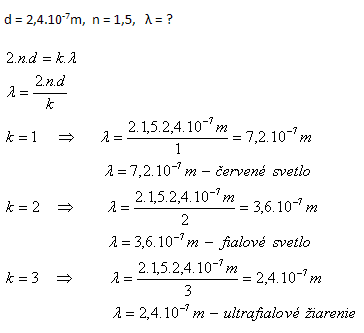
Interferencí odrazem se zruší červené a fialové světlo a neviditelné ultrafialové záření.
4.Skleněná deska s indexem lomu n = 1,5 a tloušťkou d = 0,25μm je osvětlena světlem. Jakou vlnovou délku bude mít světlo maximálně zesílené v odraženém světle?
Pro zobrazení řešení se přihlaste.
5.Kolik interferenčních maxim se vytvoří ohybem světla na mřížce, která má 5000 rýh na 1 cm, dopadá-li na ni oranžové světlo s λ = 600 nm?
Pro zobrazení řešení se přihlaste.
6.Na ohybovou mřížku, která má 100 rýh na 1 mm, dopadá kolmo paprsek světla červené složky spektra (λ = 700 nm). Určete, v jaké vzájemné vzdálenosti „h“ bude první a třetí světlý pás na stínítku, které je od zdroje světla vzdálené l = 1,5 m?
Pro zobrazení řešení se přihlaste.
7.Kolik rýh na 1 mm má optická mřížka, jestliže se světlo o vlnové délce λ = 589 nm ve druhém maximu odchyluje od směru kolmého na rovinu mřížky o úhel α = 43015‘
Pro zobrazení řešení se přihlaste.
8.Jaká musí být maximální tloušťka vzduchové vrstvy, při které by bylo možné pozorovat ve světle s vlnovou délkou 500 nm interferenční obraz vzniklý odrazem paprsků na rozhraní této vrstvy?
Pro zobrazení řešení se přihlaste.9.Dvě koherentní světelné vlny s vlnovou délkou 600 nm se setkávají v jednom bodě. Zjistěte, zda v něm nastane interferenční maximum nebo minimum, je-li jejich fázový rozdíl:
- a.) 300 nm
- b.) 600 nm
- c.) 900 nm
10. Na vrstvu oleje tloušťky d = 0,2 μm na vodě kolmo dopadá bílé světlo. Rychlost světla v oleji je
v = 2.108 m·s–1. Která barva se nejvíce zesílí a která zruší v intervalu λ : 3,8·10–7m – 7,8·10–7m.
11.Určete tloušťku mýdlové blány (n = 1,33) v místech, ve kterých vidíme blánu v odraženém světle jako modrou. Vlnová délka světla modré barvy je λ = 450 nm = 450·10–9 m = 4,5·10–7 m
Pro zobrazení řešení se přihlaste.
12.Na optickou mřížku dopadá kolmo monofrekvenční světlo. Na stínítku vzdáleném l = 1 m vzniká maximum prvního řádu ve vzdálenosti h = 2 cm od maxima nultého řádu. Jaká je vlnová délka světla, jestliže
d = 20 μm.
13.Úzký svazek bílého světla dopadá na optickou mřížku, která má N1 = 1000 rýh na 1 mm. Jak by se změnil obraz na stínítku, kdybychom mřížku vyměnili za jinou, která má N2 = 1500 rýh na 1 mm.
Pro zobrazení řešení se přihlaste.14.Clona s velmi malými otvory, jejichž středy jsou ve vzájemné vzdálenosti 1 mm, je umístěna kolmo před zdrojem monochromatického světla s λ = 500 nm. Jaká je vzájemná vzdálenost tmavých interferenčních proužků, které vznikly na stínítku? Vzdálenost otvorů od stínítka je 2,5 m.
Pro zobrazení řešení se přihlaste.15.Na ohybovou mřížku, která má 500 rýh na mm, dopadá monochromatické světlo s vlnovou délkou
λ = 5·10–7 m. Určete nejvyšší řád spektra, který lze rozeznat při kolmém dopadu paprsků na mřížku.
16.Jaká je mřížková konstanta mřížky, pokud při osvětlení světlem s vlnovou délkou λ = 590 nm bylo na stínítku vzdáleném l = 2 m od mřížky vytvořeno maximum 1. řádu ve vzdálenosti h = 66 cm od maxima nultého řádu?
Pro zobrazení řešení se přihlaste.17.Na ohybovou mřížku, která má 100 rýh na 1 mm, dopadá kolmo rovnoběžný svazek světla červené barvy (λ = 700 nm). Určete, v jaké vzájemné vzdálenosti budou 1. a 3. světlý pás na stínítku umístěném ve vzdálenosti 100 cm od mřížky.
Pro zobrazení řešení se přihlaste.18.Mřížkovým spektroskopem se získalo mřížkové spektrum. Ohybové maximum 2. řádu vzniklo ve směru odchýleného paprsku o úhel α = 300. Mřížka byla ozářena monochromatickým světlem s vlnovou délkou
λ = 5,76·10–7 m. Určete mřížkovou konstantu mřížky. Kolik rýh má mřížka na 1 mm?