Ideální plyn
1. Vysvětlete vlastnosti ideálního plynu
Řešení:
Ideální plyn není skutečný plyn, je to model plynu. Jeho molekuly mají zanedbatelné rozměry a stejné hmotnosti m0. Vzájemné srážky molekul a jejich nárazy na stěny nádoby jsou dokonale pružné. Nárazy molekul na stěny nádoby jsou příčinou tlaku plynu. Molekuly na sebe navzájem silově nepůsobí. Za "normálních podmínek" (p0 = 101325 Pa T0 = 273,15 K) se vlastnosti skutečných plynů přibližují k vlastnostem ideálního plynu. Za těchto podmínek 1mol jakéhokoliv plynu má vždy objem V0 = 22,415.10-3m3.mol-1
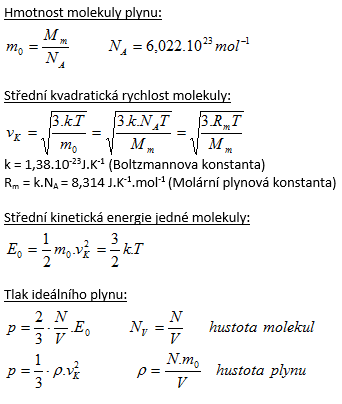
2.Vypočtěte střední kvadratickou rychlost molekuly kyslíku O2 při teplotě 0oC!
Řešení:
Rozbor:
T = t + 273,15
T = 0 + 273,15 = 273,15
m0 = Ar.mu = 2.16,00.1,66.10-27= 53,12.10-27kg
k = 1,38.10-23J.K-1
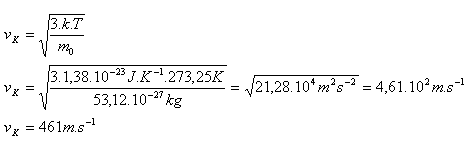
Střední kvadratická rychlost molekuly O2 je vK = 461 m.s-1
3.Určete poměr středních kvadratických rychlostí molekul vodíku H2 a kyslíku O2 při stejné teplotě.
Řešení:
Rozbor:
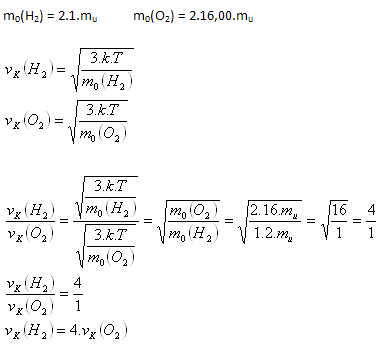
Molekuly vodíku se budou pohybovat 4 krát rychleji než molekuly kyslíku.
4.Jaký je tlak vzduchu při teplotě T = 273,15 K, jestliže hmotnost molekuly vzduchu je m0 = 47,45.10-27kg a hustota vzduchu při této teplotě je ρ = 1,27584 kg.m3.
Řešení:
Rozbor:
T = 273,15 K, m0 = 47,45.10-27kg, ρ = 1,27548 kg.m-3.

Tlak vzduchu při teplotě T = 273,15 K je p0 = 101325 Pa. Je to takzvaný "normální tlak" vzduchu.
5.Ideální plyn o hmotnosti m = 3,8.10-2kg je uzavřen v nádobě o objemu 10 litrů a má tlak p = 0,49 MPa. Určitě střední kvadratickou rychlost molekul plynu.
Řešení:
Rozbor:
m = 3,8.10-2kg, p = 0,49.106Pa, V = 10 litrov = 10-2m3

Kvadratická rychlost plynu je vK = 622 m.s-1
6.Vypočítejte při jaké teplotě je střední kvadratická rychlost helia 1300 m.s-1 vk = 1300 m.s-1, Ar(He) = 4,003, NA = 6,022.1023mol-1, k = 1,38.10-23JK-1
Řešení:
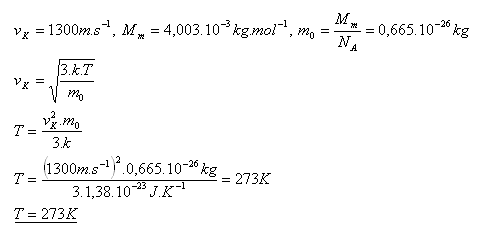
7.Jak se změní střední kinetická energie, kterou má molekula ideálního plynu v důsledku neuspořádaného pohybu, pokud se termodynamická teplota zvýší 3 krát?
Řešení:
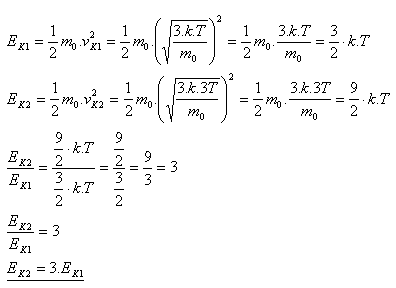
Energie se zvětší 3 krát.
8.Určete změnu vnitřní energie ideálního plynu s monoatomového molekulami, pokud se jeho teplota zvýší z 200K na 400K. V plyne je 1028molekul.
Řešení:
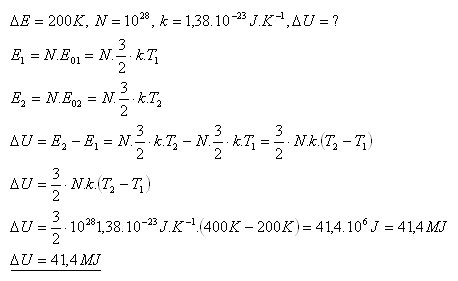
Vnitřní energie se zvýší o 41,4 MJ.
9.Jak se změní tlak ideálního plynu, jestliže hustota molekul tohoto plynu NV se zvětší 4 krát a střední kvadratická rychlost vK se nezmění.
Řešení:
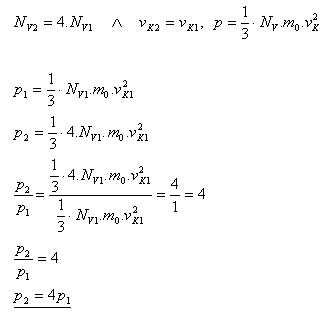
Tlak ideálního plynu se zvětší 4 krát.
10.Jaký tlak má kyslík O2 s hustotou 1,41 kg.m-3 při teplotě 00C, pokud jeho střední kvadratická rychlost je vK = 461m.s-1?
Řešení:
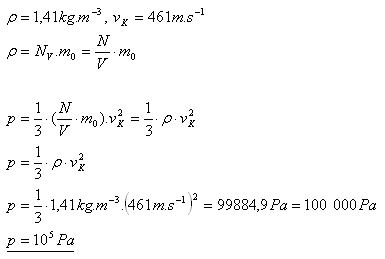
Tlak kyslíku je 105 Pa.
11.Ideální plyn o hmotnosti 6 kg je uzavřen v nádobě s objemem 5m3 při tlaku 2.105Pa. Určitě střední kvadratickou rychlost molekul plynu.
Řešení:
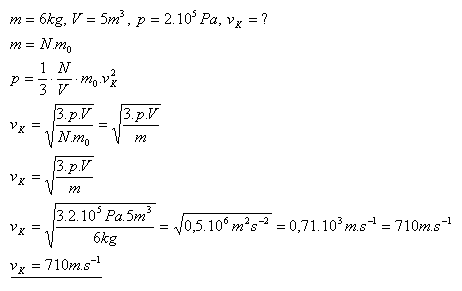
Střední kvadratickou rychlost molekul plynu je 10m.s-1.
12.Atom argonu pohybující se rychlostí 500 ms-1 se pružně odráží od stěny nádoby. Vektor rychlosti argonu zvíře s kolmicí na stěnu nádoby úhel a.) 00, b). 600. Určitě v obou případech velikost změny jeho hybnosti po dokonale pružném odrazu od stěny nádoby.
Řešení:
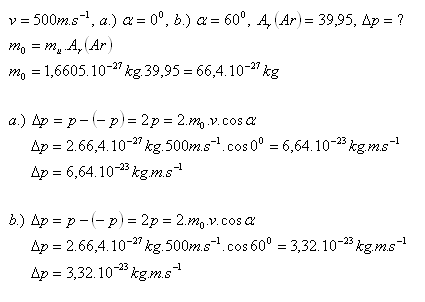
13.Střední kvadratická rychlost molekul chloru Cl2 při 00C je 310 m.s-1. Vypočtěte hustotu chloru při tlaku 105Pa.
Řešení:
Rozbor:
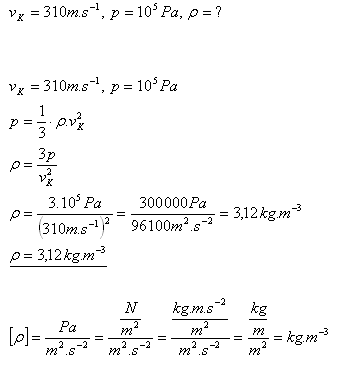
Hustota chlóru Cl2 je 3,12 kg.m-3.
14. Jakou střední kinetickou energii má molekula ideálního plynu při teplotě -1000C ?
Řešení:
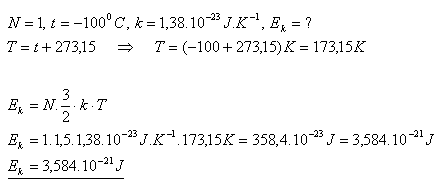
Střední kinetická energie molekuly ideálního plynu je asi 3,6.10-21J.