Ideálny plyn
1. Vysvetlite vlastnosti ideálneho plynu
Riešenie:
Ideálny plyn nie je skutočný plyn, je to model plynu. Jeho molekuly majú zanedbateľné rozmery a rovnaké hmotnosti m0. Vzájomné zrážky molekúl a ich nárazy na steny nádoby sú dokonale pružné. Nárazy molekúl na steny nádoby sú príčinou tlaku plynu. Molekuly na seba navzájom silovo nepôsobia. Za „normálnych podmienok“ (p0 = 101325 Pa T0 = 273,15 K) sa vlastnosti skutočných plynov približujú k vlastnostiam ideálneho plynu. Za týchto podmienok 1mol akéhokoľvek plynu má vždy objem V0 = 22,415.10-3m3.mol-1
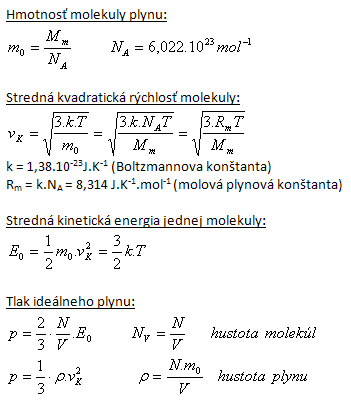
2.Vypočítajte strednú kvadratickú rýchlosť molekuly kyslíka O2 pri teplote 0oC!
Riešenie:
Rozbor:
T = t + 273,15
T = 0 + 273,15 = 273,15
m0 = Ar.mu = 2.16,00.1,66.10-27= 53,12.10-27kg
k = 1,38.10-23J.K-1
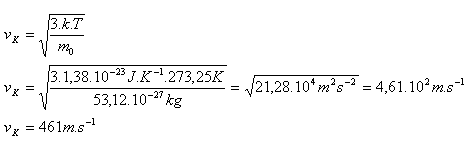
Stredná kvadratická rýchlosť molekuly O2 je vK = 461 m.s-1
3.Určite pomer stredných kvadratických rýchlostí molekúl vodíka H2 a kyslíka O2 pri rovnakej teplote.
Riešenie:
Rozbor:
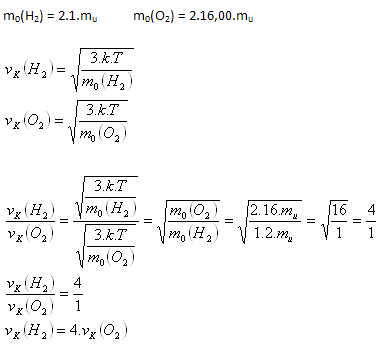
Molekuly vodíka sa budú pohybovať 4 krát rýchlejšie ako molekuly kyslíka.
4.Aký je tlak vzduchu pri teplote T = 273,15 K, ak hmotnosť molekuly vzduchu je m0 = 47,45.10-27kg a hustota vzduchu pri tejto teplote je ρ = 1,27584 kg.m3.
Riešenie:
Rozbor:
T = 273,15 K, m0 = 47,45.10-27kg, ρ = 1,27548 kg.m-3.

Tlak vzduchu pri teplote T = 273,15 K je p0 = 101325 Pa. Je to takzvaný „normálny tlak“ vzduchu.
5.Ideálny plyn s hmotnosťou m = 3,8.10-2kg je uzavretý v nádobe s objemom 10 litrov a má tlak p = 0,49 MPa. Určite strednú kvadratickú rýchlosť molekúl plynu.
Riešenie:
Rozbor:
m = 3,8.10-2kg, p = 0,49.106Pa, V = 10 litrov = 10-2m3

Kvadratická rýchlosť plynu je vK = 622 m.s-1
6.Vypočítajte pri akej teplote je stredná kvadratická rýchlosť hélia 1300 m.s-1 vk = 1300 m.s-1, Ar(He) = 4,003, NA = 6,022.1023mol-1, k = 1,38.10-23JK-1
Riešenie:
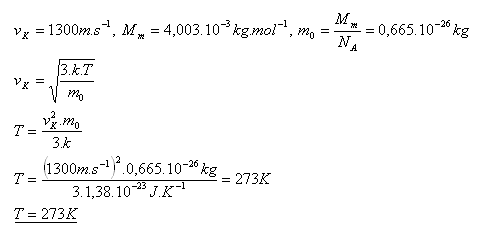
7.Ako sa zmení stredná kinetická energia, ktorú má molekula ideálneho plynu v dôsledku neusporiadaného pohybu, ak sa termodynamická teplota zvýši 3 krát
Riešenie:
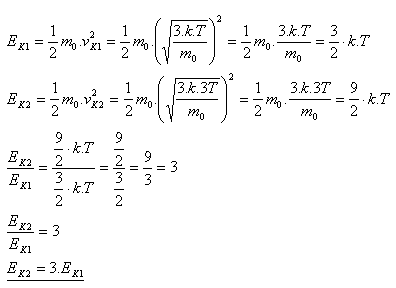
Energia sa zväčší 3 krát.
8.Určite zmenu vnútornej energie ideálneho plynu s jednoatomovými molekulami , ak sa jeho teplota zvýši z 200K na 400K. V plyne je 1028molekúl.
Riešenie:
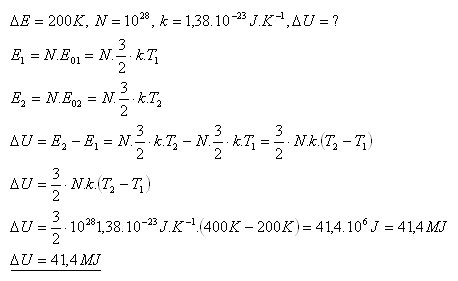
Vnútorná energia sa zvýši o 41,4 MJ.
9.Ako sa zmení tlak ideálneho plynu, ak hustota molekúl tohto plynu NV sa zväčší 4 krát a stredná kvadratická rýchlosť vK sa nezmení.
Riešenie:
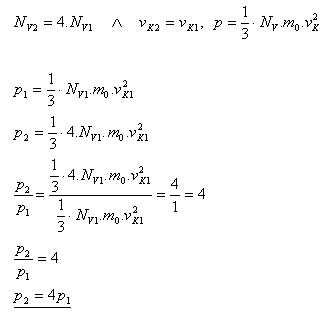
Tlak ideálneho plynu sa zväčší 4 krát.
10.Aký tlak má kyslík O2 s hustotou 1,41 kg.m-3 pri teplote 00C, ak jeho stredná kvadratická rýchlosť je vK = 461m.s-1?
Riešenie:
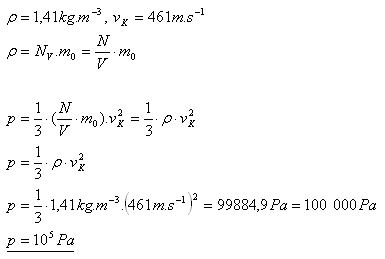
Tlak kyslíka je 105 Pa.
11.Ideálny plyn s hmotnosťou 6 kg je uzavretý v nádobe s objemom 5m3 pri tlaku 2.105Pa. Určite strednú kvadratickú rýchlosť molekúl plynu.
Riešenie:
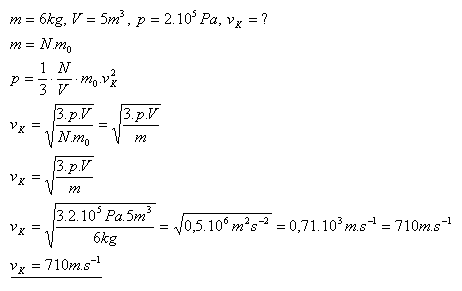
Strednú kvadratickú rýchlosť molekúl plynu je 710m.s-1.
12.Atóm argónu pohybujúci sa rýchlosťou 500 m.s-1sa pružne odráža od steny nádoby. Vektor rýchlosti argónu zviera s kolmicou na stenu nádoby uhol a.) 00 , b.) 600. Určite v obidvoch prípadoch veľkosť zmeny jeho hybnosti po dokonale pružnom odraze od steny nádoby.
Riešenie:
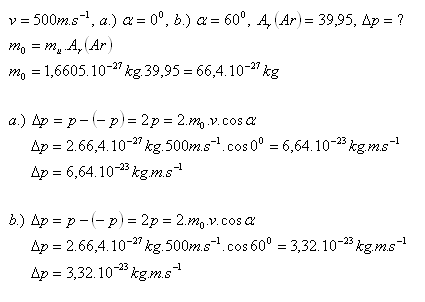
13.Stredná kvadratická rýchlosť molekúl chlóru Cl2 pri 00C je 310 m.s-1. Vypočítajte hustotu chlóru pri tlaku 105Pa.
Riešenie:
Rozbor:
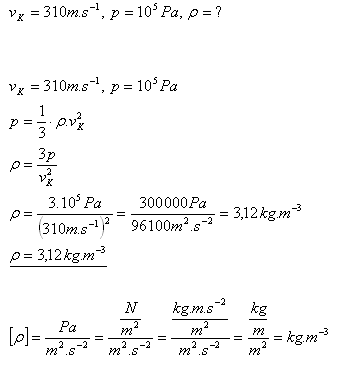
Hustota chlóru Cl2 je 3,12 kg.m-3.
14. Akú strednú kinetickú energiu má molekula ideálneho plynu pri teplote -1000C ?
Riešenie:
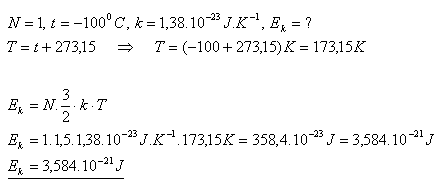
Stredná kinetická energia molekuly ideálneho plynu je asi 3,6.10-21J.