Tuhé teleso
1.Čo vieme o vlastnostiach tuhého telesa?
Riešenie:
Tuhé teleso je ideálne teleso, ktorého tvar a objem sa účinkom vonkajších síl nemení. Vonkajšie sily spôsobujú zmenu pohybového stavu tuhého telesa. Pohyb telesa môže byť:

2.Vo vrcholoch obdĺžnikovej platne so stranami a=30 cm, b=40 cm pôsobia sily F1=10 N, F2=20 N, F3=30 N, F4=40 N. Platňa je otáčavá okolo osi, ktorá je kolmá na platňu a prechádza vrcholom A. Aký je výsledný moment síl pôsobiacich na platňu?
Riešenie:
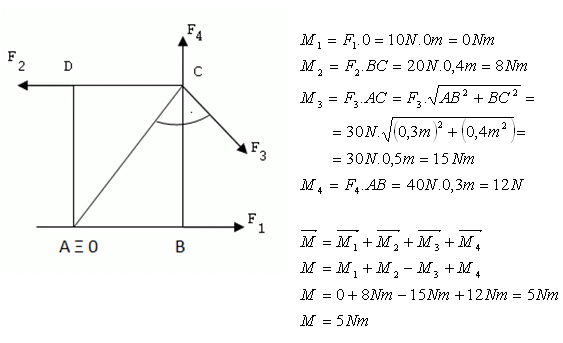
Výsledný moment síl je 5 Nm.
3.Obdĺžniková doska o rozmeroch a = 20 cm, b = 10 cm je upevnená tak, že sa môže otáčať okolo osi prechádzajúcej jej stredom O kolmo k doske. Sila F1 = 800 N. Vypočítajte veľkosť sily F2, aby doska zostala v kľude.
Riešenie:
Rozbor:
a = 20 cm =0,2 m, b =10 cm =0,1 m, r1 = 0,1 m, r2 = 0,05 m, F1 = 800 N
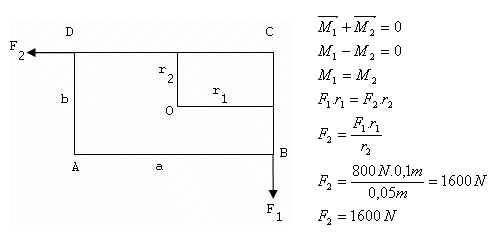
Aby doska ostala v kľude, musí byť sila F2 = 1600 N
4.Tyč má dĺžku 1,2 m. Na jej koncoch sú zavesené závažia s hmotnosťami 5 kg a 7 kg. Kde treba tyč podoprieť, aby zostala v rovnováhe?
Riešenie:
Rozbor:
r = 1,2 m, m1 = 5 kg, m2 = 7 kg, F1= 50N, F2= 70N
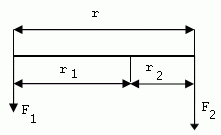 r1+r2=r
r1+r2=r
F1.r1=F2.r2
r1+r2=1,2 => r2=1,2-r1
50.r1=70.r2
50.r1=70.(1,2-r1)
50r1=84-70r1
120r1=84
r1=0,7m , r2=0,5m
Tyč treba podoprieť vo vzdialenosti 0,7 metra od sily F1.
5.Na otáčavom kotúči sú na tej istej strane od osi otáčania zavesené závažia hmotnosti m1 = 0,5kg vo vzdialenosti r1 = 0,2 m od osi otáčania a m2 = 0,2 kg vo vzdialenosti r2 = 0,4 m od osi otáčania. V akej vzdialenosti od osi musíme na druhej strane zavesiť závažie hmotnosti m3 = 0,6 kg, aby nastala rovnováha?
Riešenie:
Rozbor:
m1 = 0,5 kg, m2 = 0,2 kg, m3 = 0,6 kg, F1= 5 N, F2 = 2N, F3 = 6N, r1 = 0,2 m, r2 = 0,4 m, x = ?
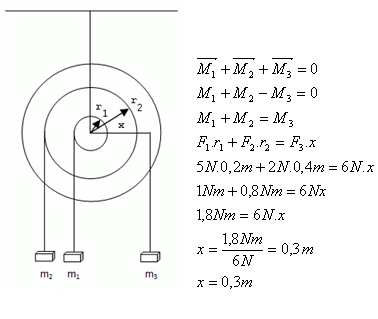
Protizávažie treba upevniť vo vzdialenosti x = 0,3 m od osi otáčania.
6.Akú veľkú prácu musíme vykonať, aby sme oceľový valec o hmotnosti 800 kg a polomerom podstavy 0,5 m roztočili na 48 otáčok za minútu? Moment zotrvačnosti plného valca: (Tabuľky)
Riešenie:
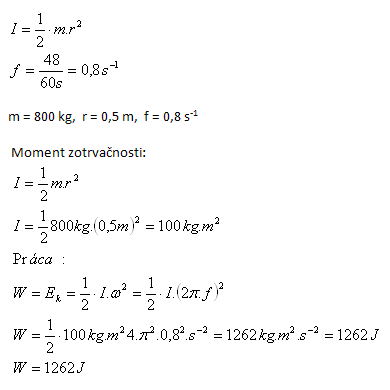
Musíme vykonať prácu W = 1262 J.
7. Aký je moment zotrvačnosti zotrvačníka, ak pri brzdení prácou 1260 J klesnú jeho otáčky z 320 min-1 na 254 min-1
Riešenie:
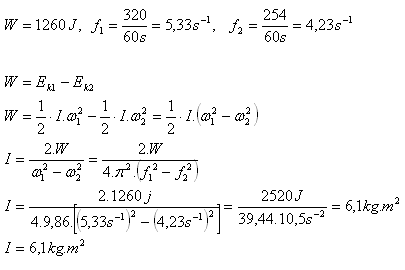
Moment zotrvačníka je asi I = 6,1 kg.m2.
8.Oceľový kotúč bol roztočený povrazom dĺžky 80 cm, na ktorý pôsobila sila 30 N. Koľko otáčok vykoná za 1 sekundu, ak jeho moment zotrvačnosti je 0,03 kg.m2?
Riešenie:
Rozbor:
l = 80 cm = 0,8 m, F = 30 N, I = 0,03 kg.m2, f = ?
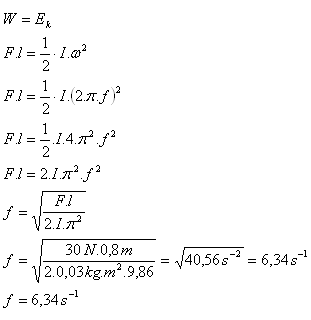
Oceľový kotúč vykoná 6,34 otáčok za sekundu.
9. Do akej výšky by vystúpilo detské autíčko idúce hore kopcom, poháňané len zotrvačníkom s momentom zotrvačnosti 0,1 kg.m2. Zotrvačník vykonáva 4 otáčky za sekundu. Hmotnosť autíčka je 8 kg.
Riešenie:
Rozbor:
I = 0,1 kg.m2, f = 4s-1, m = 8 kg, h = ?
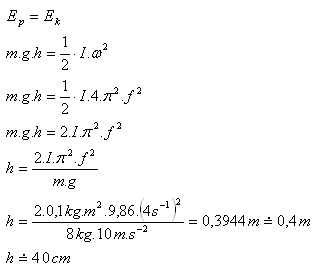
Autíčko vystúpi do výšky h = 40 cm.
10.Určite najmenšiu frekvenciu, na ktorú sa musí roztočiť zotrvačník s momentom zotrvačnosti 305 kg.m2, aby za čas 10 minút dodával výkon 25 kW.
Riešenie:
Rozbor:
I = 305 kg.m2, t = 10 min. = 600 s, P = 25 000 W, f = ?
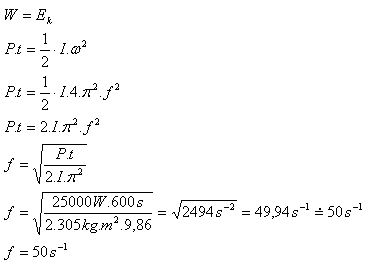
Najmenšia frekvencia zotrvačníka je f = 50 s-1.
11.Vysvetlite, kedy pri výpočte momentu zotrvačnosti tuhého telesa použijeme Steinerovu vetu?
Riešenie:
Ak os rotácie tuhého telesa neprechádza ťažiskom, platí Steinerova veta.
I = I0 + m.d2
I0 – moment zotrvačnosti telesa, ak os rotácie prechádza ťažiskom
m – hmotnosť telesa
d – vzdialenosť ťažiska od osi rotácie
Moment zotrvačnosti niektorých telies:
12.Vypočítajte moment zotrvačnosti plnej homogénnej gule s polomerom r = 10 cm, hmotnosti 25 kg vzhľadom na os, ktorá sa dotýka povrchu gule.
Riešenie:
Rozbor:
r = 10 cm = 0,1m, m = 25kg, d = r = 0,1m
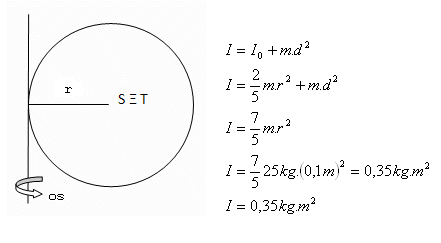
Moment zotrvačnosti gule je I = 0.35 kg.m2.
13. Určite dĺžku tyče l, ktorej hmotnosť je 1,2 kg, modul zotrvačnosti 0,592 kg.m2, ak sa tyč otáča vo vzdialenosti 0,4 m od pevnej osi.
Riešenie:
Rozbor:
m = 1,2 kg, I = 0,592 kg.m2, d = 0,4 m, l = ?
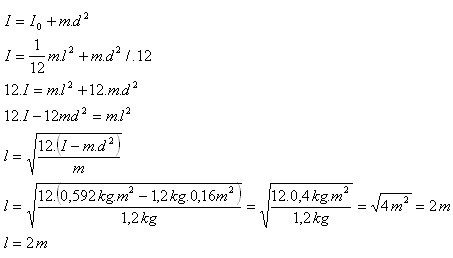
Dĺžka tyče je l = 2 m.
14.Plné koleso (kruhový kotúč) o hmotnosti 20 kg a polomerom r = 50 cm sa kotúľa (valí) rýchlosťou 10 m.s-1. Akú má kinetickú energiu?
Riešenie:
Rozbor:
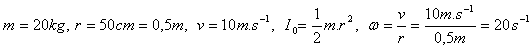
Valivý pohyb je zložený z posuvného a rotačného pohybu. Platí: 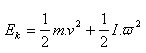
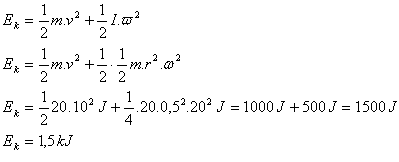
Kinetická energia kolesa je Ek = 1,5 kJ.
15.Akú rýchlosť získa guľa, ktorá sa kotúľa po naklonenej rovine z výšky 1 m?
Riešenie:
Rozbor:
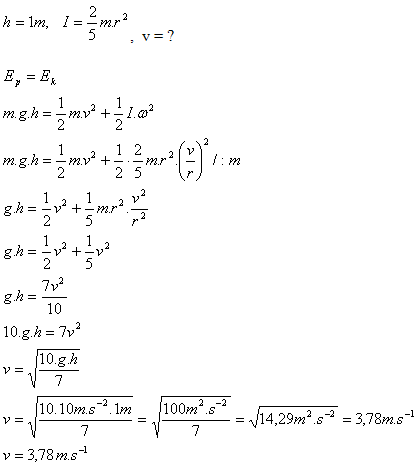
Guľa získa rýchlosť v = 3,78 m.s-1