Tuhé těleso
1.Co víme o vlastnostech tuhého tělesa?
Řešení:
Tuhé těleso je ideální těleso, jehož tvar a objem se účinkem vnějších sil nemění. Vnější síly způsobují změnu pohybového stavu tuhého tělesa. Pohyb tělesa může být:
2.Ve vrcholech obdélníkové desky se stranami a = 30 cm, b = 40 cm působí síly F1 = 10 N, F2 = 20 N, F3 = 30 N, F4 = 40 N. Deska je otáčivá kolem osy, která je kolmá na desku a prochází vrcholem A. Jaký je výsledný moment sil působících na plotnu?
Řešení:
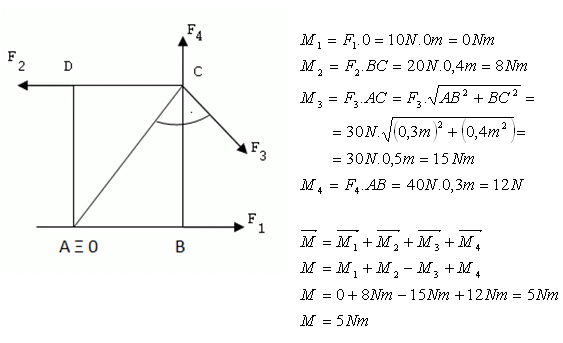
Výsledný moment sil je 5 Nm.
3.Obdélníková deska o rozměrech a = 20 cm, b = 10 cm je upevněna tak, že se může otáčet kolem osy procházející jejím středem O kolmo k desce. Síla F1 = 800 N. Vypočtěte velikost síly F2, aby deska zůstala v klidu.
Řešení:
Rozbor:
a = 20 cm =0,2 m, b =10 cm =0,1 m, r1 = 0,1 m, r2 = 0,05 m, F1 = 800 N
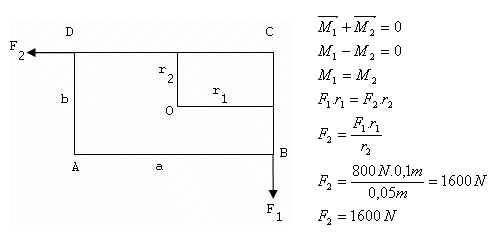
Aby deska zůstala v klidu, musí být síla F2 = 1600 N
4.Tyč má délku 1,2 m. Na její koncích jsou zavěšeny závaží s hmotnostmi 5 kg a 7 kg. Kde je třeba tyč podepřít, aby zůstala v rovnováze?
Řešení:
Rozbor:
r = 1,2 m, m1 = 5 kg, m2 = 7 kg, F1= 50N, F2= 70N
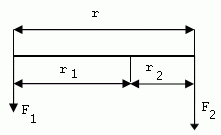r1+r2=r
F1.r1=F2.r2
r1+r2=1,2 => r2=1,2-r1
50.r1=70.r2
50.r1=70.(1,2-r1)
50r1=84-70r1
120r1=84
r1=0,7m , r2=0,5m
Tyč třeba podepřít ve vzdálenosti 0,7 metru od síly F1.
5.Na otáčivém kotouči jsou na téže straně od osy otáčení zavěšené závaží hmotnosti m1 = 0,5 kg ve vzdálenosti r1 = 0,2 m od osy otáčení a m2 = 0,2 kg ve vzdálenosti r2 = 0,4 m od osy otáčení. V jaké vzdálenosti od osy musíme na druhé straně zavěsit závaží hmotnosti m3 = 0,6 kg, aby nastala rovnováha?
Řešení:
Rozbor:
m1 = 0,5 kg, m2 = 0,2 kg, m3 = 0,6 kg, F1= 5 N, F2 = 2N, F3 = 6N, r1 = 0,2 m, r2 = 0,4 m, x = ?
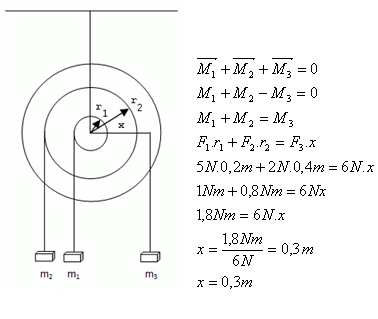
Protizávaží třeba upevnit ve vzdálenosti x = 0,3 m od osy otáčení.
6.Jak velkou práci musíme vykonat, abychom ocelový válec o hmotnosti 800 kg a poloměru podstavy 0,5 m roztočili na 48 otáček za minutu? Moment setrvačnosti plného válce: (Tabulky)
Řešení:
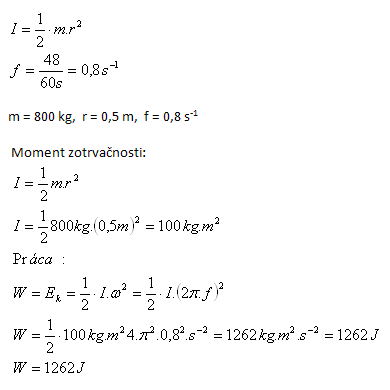
Musíme vykonat práci W = 1262 J.
7. Jaký je moment setrvačnosti setrvačníku, pokud při brzdění prací 1260 J klesnou jeho otáčky z 320 min-1 na 254 min-1
Řešení:
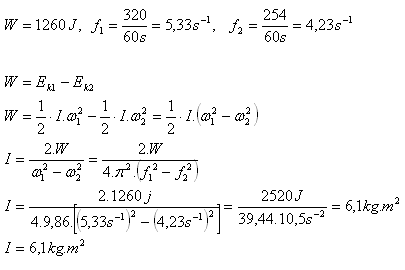
Moment setrvačníku je asi I = 6,1 kg.m2.
8.Ocelový kotouč byl roztočený provazem délky 80 cm, na který působila síla 30 N. Kolik otáček vykoná za 1 sekundu, pokud jeho moment setrvačnosti je 0,03 kg.m2?
Řešení:
Rozbor:
l = 80 cm = 0,8 m, F = 30 N, I = 0,03 kg.m2, f = ?
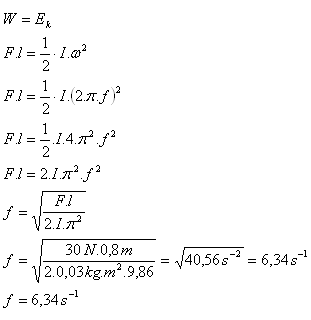
Ocelový kotouč provede 6,34 otáček za sekundu.
9. Do jaké výšky by vystoupilo dětské autíčko jdoucí nahoru kopcem, poháněné pouze setrvačníkem s momentem setrvačnosti 0,1 kg.m2. Setrvačník provádí 4 otáčky za sekundu. Hmotnost autíčka je 8 kg.
Řešení:
Rozbor:
I = 0,1 kg.m2, f = 4s-1, m = 8 kg, h = ?
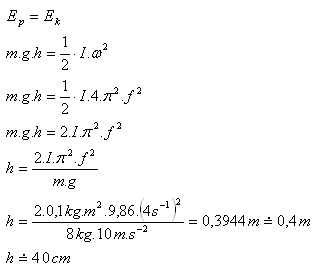
Autíčko vystoupí do výšky h = 40 cm.
10.Určete nejmenší frekvenci, na kterou se musí roztočit setrvačník s momentem setrvačnosti 305 kg.m2, aby za čas 10 minut dodával výkon 25 kW.
Řešení:
Rozbor:
I = 305 kg.m2, t = 10 min. = 600 s, P = 25 000 W, f = ?
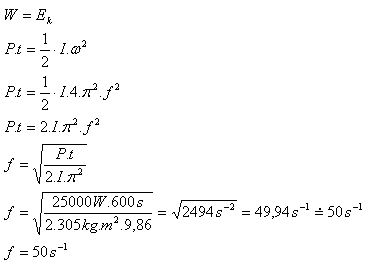
Nejmenší frekvence setrvačníku je f = 50 s-1.
11.Vysvětlete, kdy při výpočtu momentu setrvačnosti tuhého tělesa použijeme Steinerová větu?
Řešení:
Pokud osa rotace tuhého tělesa neprochází těžištěm, platí Steinerova věta.
I = I0 + m.d2
I0 – moment setrvačnosti tělesa, jestliže osa rotace prochází těžištěm
m – hmotnost tělesa
d – vzdálenost těžiště od osy rotace
Moment setrvačnosti některých těles:
12.Vypočtěte moment setrvačnosti plné homogenní koule o poloměru r = 10 cm, hmotnosti 25 kg vzhledem k ose, která se dotýká povrchu koule.
Řešení:
Rozbor:
r = 10 cm = 0,1m, m = 25kg, d = r = 0,1m
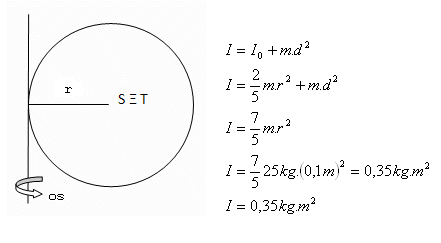
Moment setrvačnosti koule je I = 0.35 kg.m2.
13. Určete délku tyče l, jejíž hmotnost je 1,2 kg, modul setrvačnosti 0,592 kg.m2, pokud se tyč otáčí ve vzdálenosti 0,4 m od pevné osy.
Řešení:
Rozbor:
m = 1,2 kg, I = 0,592 kg.m2, d = 0,4 m, l = ?
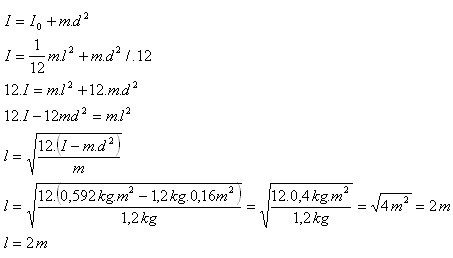
Délka tyče je l = 2 m.
14.Plné kolo (kruhový kotouč) o hmotnosti 20 kg a poloměru r = 50 cm se kutálí (valí) rychlostí 10 ms-1. Jakou má kinetickou energii?
Řešení:
Rozbor:
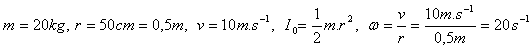
Valivý pohyb je složen z posuvného a rotačního pohybu. Platí: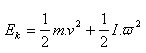 
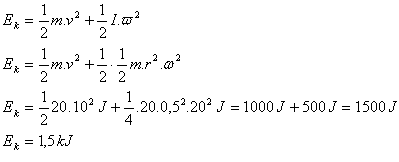
Kinetická energie kola je Ek = 1,5 kJ.
15.Jakou rychlost získá koule, která se kutálí po nakloněné rovině z výšky 1 m?
Řešení:
Rozbor:
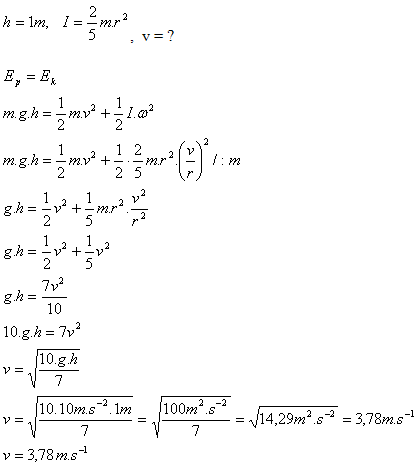
Koule získá rychlost v = 3,78 m.s-1