Rigid body
1.What do we know about the properties of a rigid body?
Solution:
A rigid body is an ideal body whose shape and volume do not change under the action of external forces. External forces cause a change in the state of motion of the rigid body. The motion of the body can be:
2.At the corners of a rectangular plate with sides a = 30 cm, b = 40 cm act forces F1 = 10 N, F2 = 20 N, F3 = 30 N, F4 = 40 N. The plate can rotate about an axis perpendicular to the plate passing through vertex A. What is the resultant moment of the forces acting on the plate?
Solution:
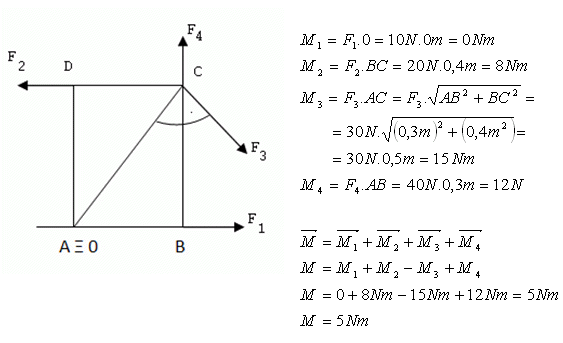
The resultant moment of the forces is 5 N·m.
3.A rectangular plate with dimensions a = 20 cm, b = 10 cm is mounted so that it can rotate about an axis passing through its center O perpendicular to the plate. Force F1 = 800 N. Calculate the magnitude of force F2 so that the plate remains at rest.
Solution:
Analysis:
a = 20 cm = 0.2 m, b = 10 cm = 0.1 m, r1 = 0.1 m, r2 = 0.05 m, F1 = 800 N
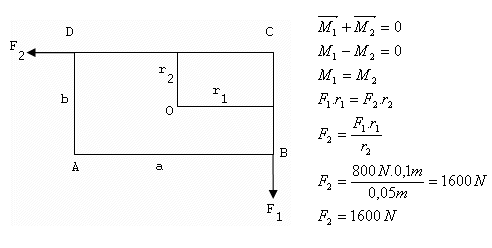
For the plate to remain at rest, the force F2 must be 1600 N.
4.The rod has length 1.2 m. Weights of mass 5 kg and 7 kg are hung on its ends. Where should the rod be supported so that it remains in equilibrium?
Solution:
Analysis:
r = 1.2 m, m1 = 5 kg, m2 = 7 kg, F1 = 50 N, F2 = 70 N
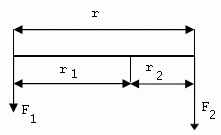r1 + r2 = r
F1·r1 = F2·r2
r1 + r2 = 1.2 ⇒ r2 = 1.2 − r1
50·r1 = 70·r2
50·r1 = 70·(1.2 − r1)
50 r1 = 84 − 70 r1
120 r1 = 84
r1 = 0.7 m, r2 = 0.5 m
The rod should be supported at a distance of 0.7 meters from force F1.
5.On a rotating pulley, weights m1 = 0.5 kg at distance r1 = 0.2 m and m2 = 0.2 kg at distance r2 = 0.4 m from the axis of rotation are hung on the same side of the rotation axis. At what distance from the axis must we hang a weight m3 = 0.6 kg on the other side so that equilibrium occurs?
Solution:
Analysis:
m1 = 0.5 kg, m2 = 0.2 kg, m3 = 0.6 kg, F1 = 5 N, F2 = 2 N, F3 = 6 N, r1 = 0.2 m, r2 = 0.4 m, x = ?
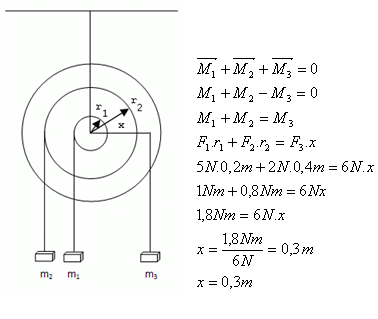
The counterweight must be attached at a distance x = 0.3 m from the axis of rotation.
6.How much work must we perform to spin a steel cylinder of mass 800 kg and base radius 0.5 m up to 48 revolutions per minute? Moment of inertia of a solid cylinder: (Tables)
Solution:
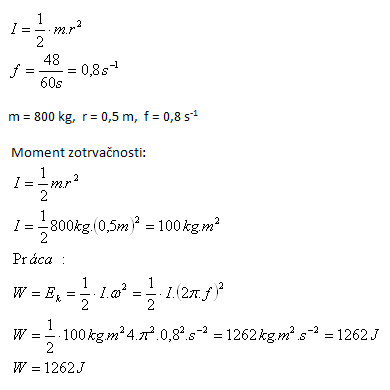
We must perform work W = 1262 J.
7.What is the moment of inertia of a flywheel if, during braking by work of 1260 J, its rotations drop from 320 min-1 to 254 min-1?
Solution:
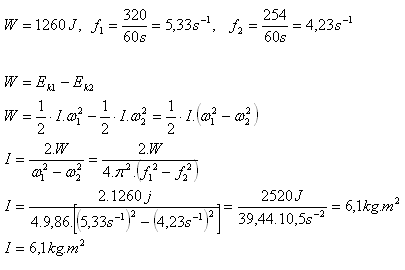
The flywheel's moment of inertia is approximately I = 6.1 kg·m2.
8.A steel disc was spun using a rope of length 80 cm on which a force of 30 N acted. How many revolutions will it make in 1 second if its moment of inertia is 0.03 kg·m2?
Solution:
Analysis:
l = 80 cm = 0.8 m, F = 30 N, I = 0.03 kg·m2, f = ?
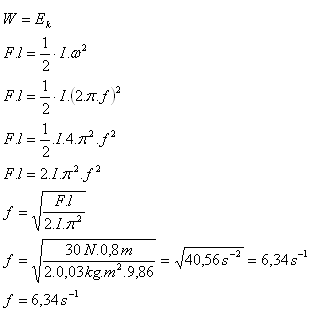
The steel disc makes 6.34 revolutions per second.
9.To what height would a toy car climb up a hill if it is driven only by a flywheel with moment of inertia 0.1 kg·m2? The flywheel makes 4 revolutions per second. The mass of the toy car is 8 kg.
Solution:
Analysis:
I = 0.1 kg·m2, f = 4 s-1, m = 8 kg, h = ?
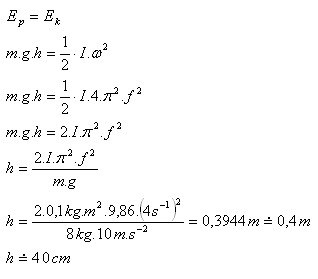
The toy car will climb to a height h = 40 cm.
10.Determine the minimum frequency that a flywheel with moment of inertia 305 kg·m2 must reach so that over a time of 10 minutes it delivers power of 25 kW.
Solution:
Analysis:
I = 305 kg·m2, t = 10 min. = 600 s, P = 25 000 W, f = ?
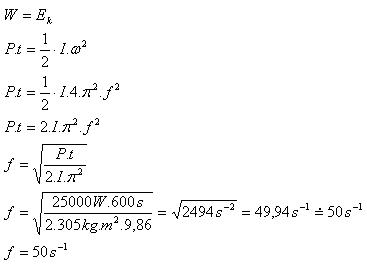
The minimum frequency of the flywheel is f = 50 s-1.
11.
Explain when we use Steiner's theorem (the parallel-axis theorem) in the calculation of the moment of inertia of a rigid body?
Solution:
If the axis of rotation of the rigid body does not pass through the center of mass, Steiner's theorem applies.
I = I0 + m·d2
I0 – moment of inertia of the body when the axis of rotation passes through the center of mass
m – mass of the body
d – distance of the center of mass from the axis of rotation
Moments of inertia of some bodies:
12.Calculate the moment of inertia of a solid homogeneous sphere with radius r = 10 cm and mass 25 kg with respect to an axis that is tangent to the surface of the sphere.
Solution:
Analysis:
r = 10 cm = 0.1 m, m = 25 kg, d = r = 0.1 m
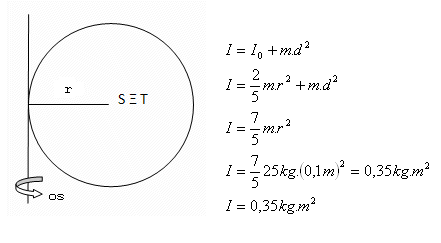
The moment of inertia of the sphere is I = 0.35 kg·m2.
13. Determine the length of the rod l whose mass is 1.2 kg and modulus of inertia is 0.592 kg·m2, if the rod rotates at a distance 0.4 m from the fixed axis.
Solution:
Analysis:
m = 1.2 kg, I = 0.592 kg·m2, d = 0.4 m, l = ?
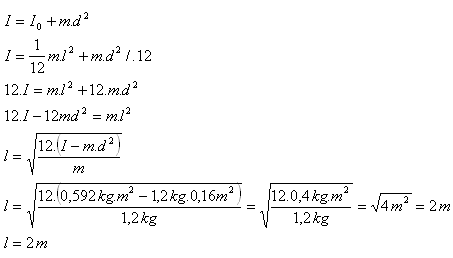
The length of the rod is l = 2 m.
14.A solid wheel (circular disc) of mass 20 kg and radius r = 50 cm rolls with speed 10 m·s-1. What is its kinetic energy?
Solution:
Analysis:
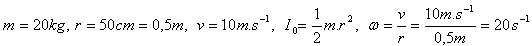
Rolling motion is composed of translational and rotational motion. It holds: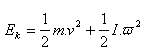 
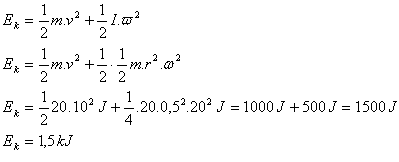
The kinetic energy of the wheel is Ek = 1.5 kJ.
15.
What speed does a sphere gain when it rolls down an inclined plane from a height of 1 m?
Solution:
Analysis:
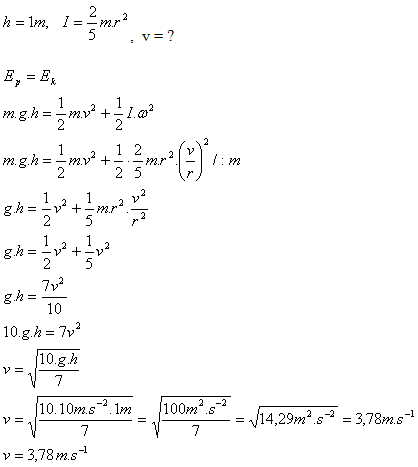
The sphere attains a speed v = 3.78 m·s-1