Power
1. Characterize the physical quantity power.
Solution:
Power is a physical quantity that characterizes the rate of doing work.
Power P is the work done per unit time.
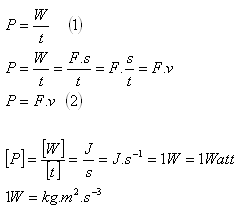
Efficiency:
The work supplied to a mechanical system per time t is called the input power Pp.
The work performed by the mechanical system per time t is called the output power P.
It holds: P < Pp ΔP = Pp – P are the losses.
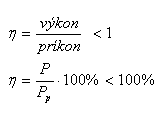
2.The elevator motor lifts a load of mass 240 kg to a height of 36 m in 90 s with uniform motion.
- a.) What is the motor’s output power?
- b.) What is its input power if η = 96% = 0.96?
Solution:
Analysis:
m = 240 kg, h = 36 m, t = 90 s, η = 96%
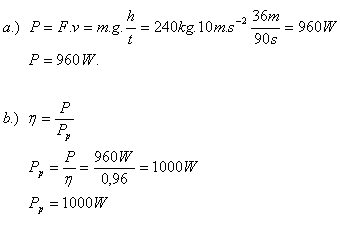
The motor has output power P = 960 W and input power Pp = 1000 W.
3.In what time will a crane, whose electric motor has input power Pp = 9000 W, lift a load of mass 12 tons to a height of 9 m with uniform motion, if the motor’s efficiency is η = 0.654?
Solution:
Analysis:
Pp = 9000 W, m = 12 t = 12 000 kg, h = 9 m, η = 0.654
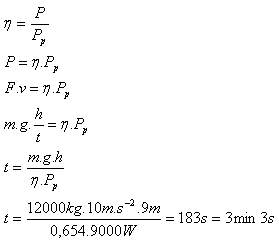
The crane will lift the load in about 3 minutes and 3 seconds.
4.An electric motor with input power 3.5 kW pumps water to a height of 30 m. How much water will it pump in 14 hours, if η = 60%?
Solution:
Analysis:
Pp = 3.5 kW = 3.5·103 W, h = 30 m, t = 14 h = 50 400 s, η = 60% = 0.6
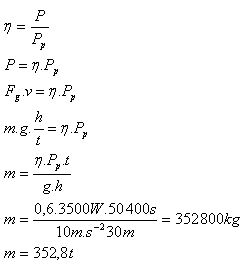
In 14 hours the motor will pump 352.8 tons of water.
5. A hiker climbs from Štrbské Pleso (1350 m a.s.l.) to Gerlachovský štít (2663 m a.s.l.). The hiker’s mass is 68 kg, the backpack he carries has a mass of 12 kg. What was his power if the ascent took 5 hours?
Solution:
Analysis:
h1 = 1350 m, h2 = 2663 m, m1 = 68 kg, m2 = 12 kg, t = 5 h = 18 000 s
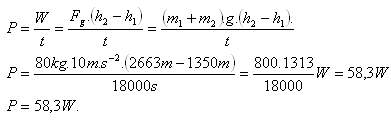
The hiker’s power was P = 58.3 W.
6. A cyclist rides up a hill at a constant speed. The crank length is 25 cm, the time for one pedal rotation is 2 s, and the average force on the pedal is 150 N. Determine the cyclist’s average power!
Solution:
Analysis:
r = 25 cm = 0.25 m, T = 2 s, F = 150 N, P = ?
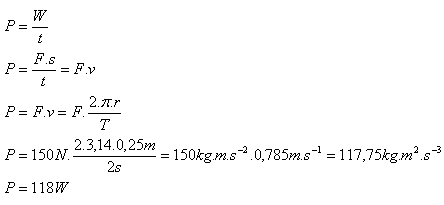
The cyclist’s power is about P = 118 W.
7.A four‑engine jet aircraft flies straight and level, covering 12 km every minute. Each engine operates at a power of 800 kW. What is the magnitude of the drag force acting on the airplane?
Solution:
Analysis:
t = 1 min = 60 s, s = 12 km = 12 000 m, P = 800 kW = 800 000 W,
4P = P´ = 3 200 000 W
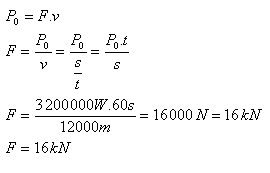
The drag force acting on the airplane is F = 16 kN.
8.A car of mass 1.5 tons accelerates for 0.5 minutes at a constant power of 22.5 kW. What speed did it reach? (Neglect friction and drag.)
Solution:
Analysis:
m = 1.5 t = 1500 kg, t = 0.5 min = 30 s, P = 22.5 kW = 22 500 W
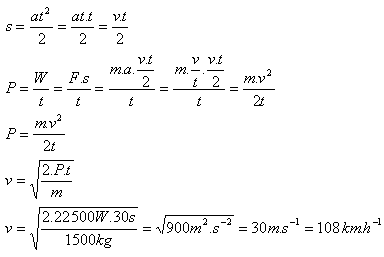
The car reached a speed of v = 108 km·h-1.
9.The water consumption for one turbine of a hydroelectric power plant is 630 m3·s-1. The turbogenerator output is 100 MW at η = 90%. Determine the difference in water levels at the dam and below the dam!
Solution:
Analysis:
P = 100 MW = 108 W, η = 90% = 0.90, ρ = 1000 kg·m-3, h2 – h1 = ?
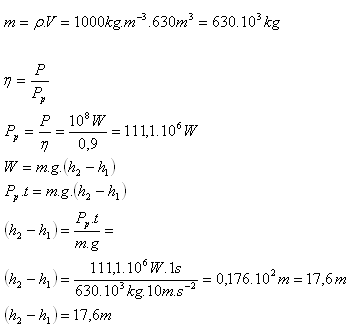
The level difference is 17.6 m.
10.A train of mass 5·105 kg moving at a speed of 72 km·h-1 begins braking until it stops.
- a.) How much heat was generated during braking, assuming all the work used for braking was converted to heat?
- b.) What was the braking power if the braking lasted 40 s?
Solution:
Analysis:
m = 5·105 kg, v = 72 km·h-1 = 20 m·s-1, t = 40 s, Q = ?, P = ?
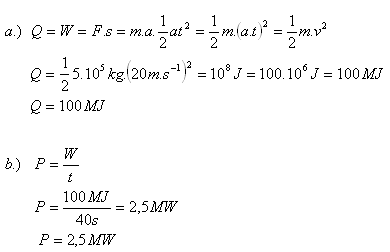
During braking, 100 MJ of heat was generated. The braking power was 2.5 MW.
11.The airplane has a mass of 3 000 kg. In 1 minute it climbs to a height of 1 km and reaches a speed of 180 km·h-1. Determine the engine power!
Solution:
Analysis:
m = 3 000 kg, h = 1 km = 1000 m, t = 1 min = 60 s, v = 180 km·h-1 = 50 m·s-1
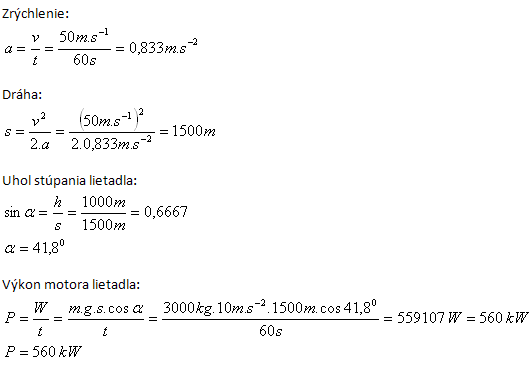
The engine power is P = 560 kW.