Two lines in a plane

1. Characterize the properties of two lines in a plane.

Solution:

Two lines p, q in a plane are:

a) distinct parallel

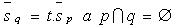
b) coincident parallel

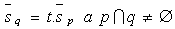
c) intersecting


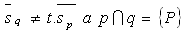
The intersection point P of two intersecting lines is determined by solving their system of equations.

The angle φ between two lines is determined as the angle between their direction (or normal) vectors, or using their slopes kp, kq


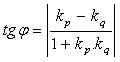
The distance d between two parallel lines is determined as the distance from a point (belonging to one line) to the other line.

The bisector of the angle between two intersecting lines is the line whose points are equidistant from both intersecting lines. (d_p = d_q)

2. Determine the mutual position of lines p and q, given:

Solution:



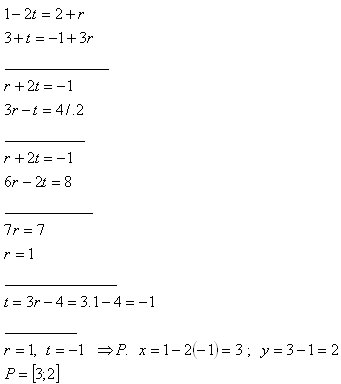
Lines p, q are intersecting and meet at point P[3;2].

3. Determine the mutual position of lines p and q, given:

Solution:



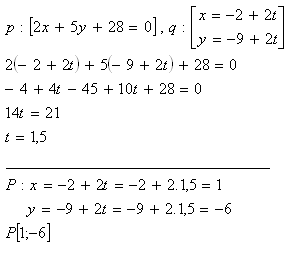
The lines are intersecting and meet at point P[1;-6].

4. The equations of the sides of triangle ΔABC are:

Solution:



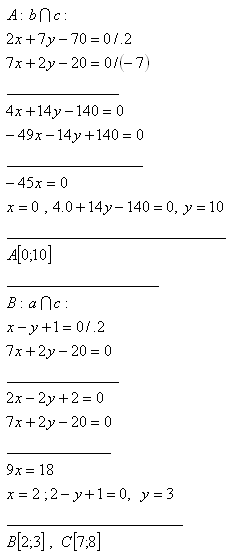
The vertices of the triangle are A[0;10], B[2;6], and C[7;8].

5. Opposite sides of a square lie on parallel lines:

Solution:



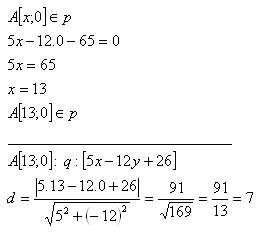
The side of the square is d = 7 units.

S = d²
S = 7²
S = 49 u²

The area of the square is S = 49 u².

6. Triangle ΔABC is defined by the sides:

Solution:

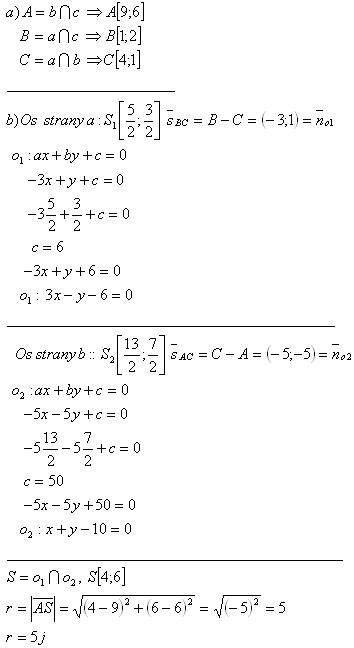
7. For point M [1;2], find point N [x;y] symmetric with respect to line p:[x – y - 1 = 0].

Solution:

The desired point N lies on line q passing through point M, perpendicular to line p.
Points M and N are equidistant from line p.
It holds:
p∩q = S, MS = SN



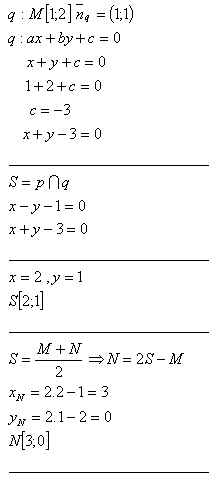
The desired point is N[3;0].

8. Write the equation of the angle bisector of the lines:

Solution:

The angle bisector of lines p and q is the line whose points are equidistant from both lines.



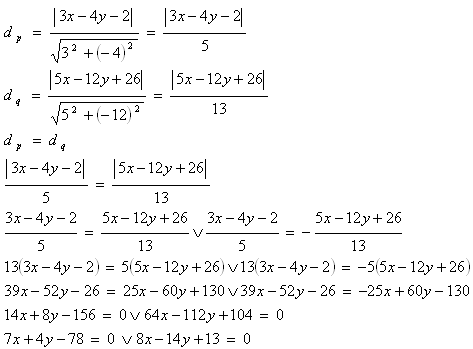
There are two angle bisectors (perpendicular to each other):
o1: [7x + 4y - 78 = 0]
o2: [8x - 14y + 13 = 0]

9. Write the equation of the line q, which passes through the point M [1;3] and forms an angle φ = 45° with the line p: [2x – y + 5 = 0].

Solution:



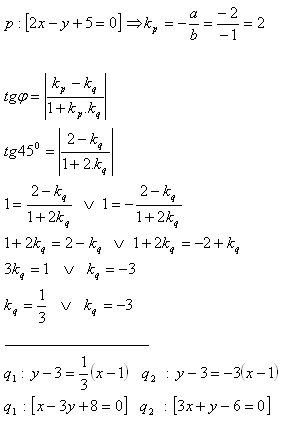
The desired lines are two:
q1: [x – 3y + 8 = 0]
q2: [3x + y – 6 = 0]

10. Three neighboring villages have the following locations on the map:

Solution:

The location of the community center is determined as the intersection of the perpendicular bisectors of the sides of triangle ΔABC.



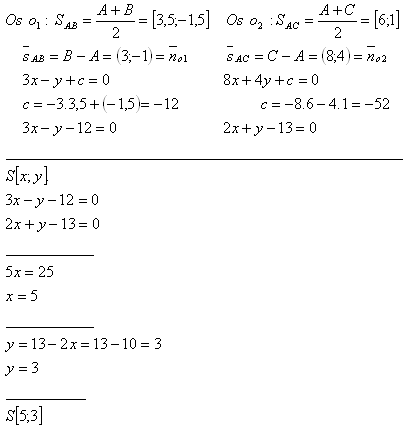
The location of the community center will be at point S[5;3].

11. Find the set of all points in the plane that are equidistant from the parallel lines:

Solution:



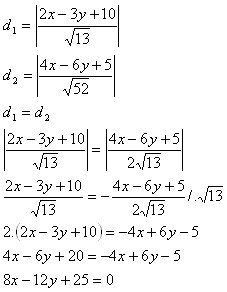
The desired set is the line o: [8x – 12y + 25 = 0].

12. On the line p: [5x – 4y - 28 = 0], determine the point that is equidistant from the points M [1;5] and N [7;-3].

Solution:

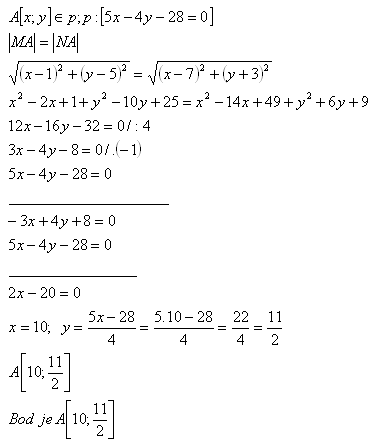
13. Determine the coordinates of the center of square ABCD, if one vertex A[-3;-4] is given and the diagonal BD lies on the line p: [3x +4y – 25 = 0].

Solution:



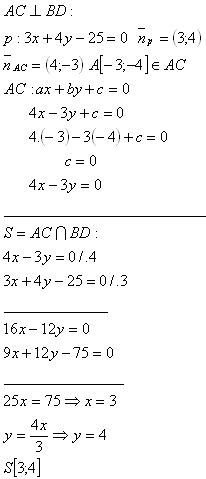
The coordinates of the center of square ABCD are S[3;4].

14. Determine the locus of points whose distances from the lines:

Solution:



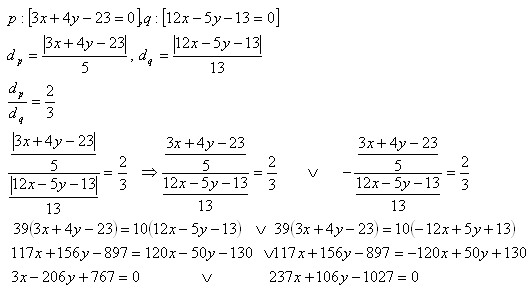
The loci of points are the lines 3x - 206y + 737 = 0 and 237x + 106y - 1027 = 0.