Conic sections
1. What do you know about conic sections:
Solution:
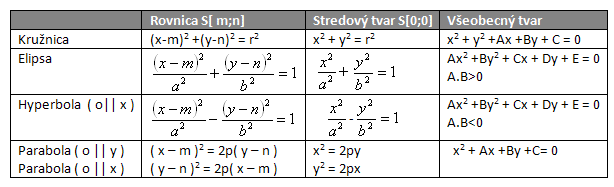
Circle is the set of points in the plane that have the same distance r from a fixed point S in the plane. S[m ; n] is the center and r is the radius of the circle.
Ellipse is the set of points in the plane for which the sum of distances from points F1, F2 of the plane is equal to 2a. Points F1[-e;0], F2[e;0] are the foci, eccentricity e2 = a2 - b2, a – semi-major axis, b – semi-minor axis.
Hyperbola is the set of points in the plane for which the absolute value of the difference of distances from points F1, F2 of the plane is equal to 2a. Points F1[-e;0], F2[e;0] are the foci, eccentricity e2 = a2 + b2. a – real, b – imaginary semi-axis. Equations of the asymptotes of the hyperbola: ( o || x ) : 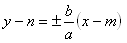
Parabola is the set of points in the plane whose distance from a point F in the plane and from a line d lying in the plane are equal. Point F is the focus of the parabola, d – the directrix. Point F does not lie on d. The value p is the parameter of the parabola.
We determine the mutual position of a conic and a line by solving the system of their equations, which leads to solving a quadratic equation. If D > 0 the line is a secant, if D = 0 the line is a tangent, if D < 0 the line does not intersect.
2.Write the equation of a circle that has radius r = 8 and is tangent to both coordinate axes.
Solution:
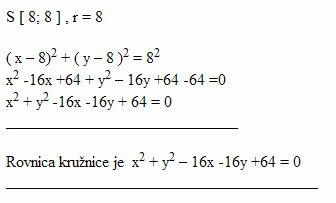
The equation of a circle is
3.Write the equation of the circle whose diameter is the segment AB, given A [-1 ; 4 ], B [ 5 ; 6 ].
Solution:
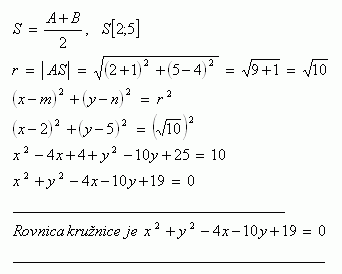
4.Prove that the equations k: x2 + y2 + 2x + 4y + 1 = 0 and k2: x2 + y2 - 8x + 6y + 9 = 0 represent circles. Write the equation of the line that passes through the centers of these circles.
Solution:
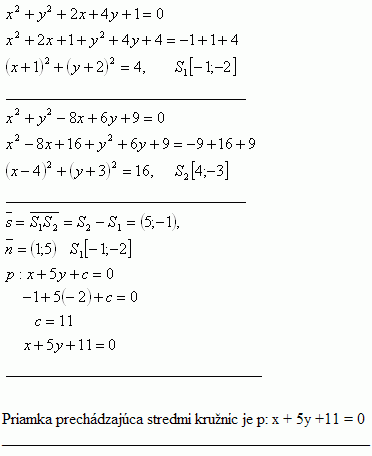
The line passing through the centers of the circles is
5.There is a circle passing through point A [4; 2] that is tangent to the coordinate axes. Write the equation of this circle.
Solution:
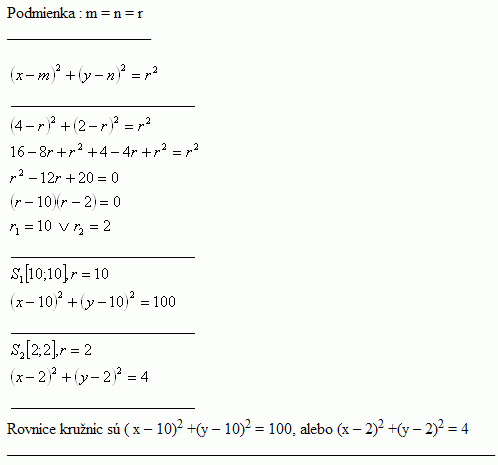
The equations of the circles are
6.Point A [-4 ; 5] is a vertex of a square whose diagonal lies on the line p : [ 7x – y + 8 = 0 ]. Write the equation of the circle circumscribed about the square.
Solution:
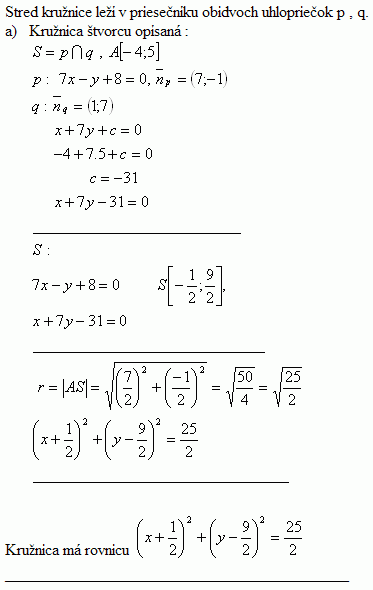
The equations of the circles is
7.Write the equation of the circle whose center S lies on the line p :[ x – y – 1 = 0 ] and that also passes through points A [ -1; -1 ] and B [ 0; 6 ].
Solution:
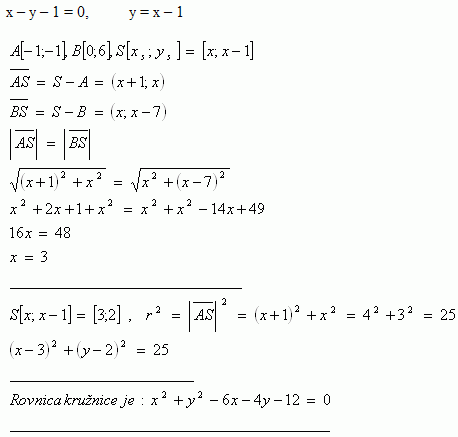
8.Write the equation of the circle that passes through points K [2;-1], L [5;-2], M [10;3].
Solution:
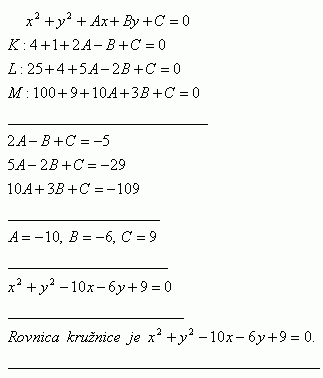
The equations of the circles is
9.Investigate the relative position of the line p: [2x – y – 6 = 0] and the circle k: [x2 + y2 – 4x -5y -1 = 0]
Solution:

A straight line is a secant of a circle, intersecting it at points
10.Write the equation of the circle symmetric to circle k1: ( x – 1 )2 + ( y – 2 )2 = 1 with respect to the line p: x – y – 3 = 0
Solution:
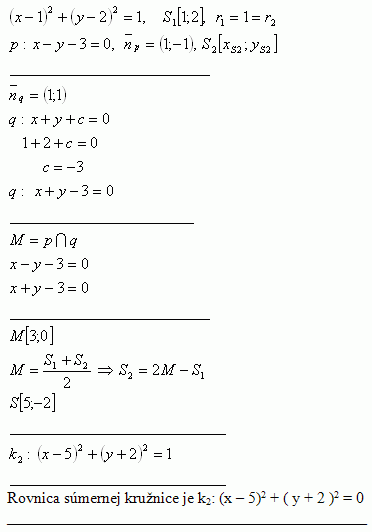
The equations of the circles is
11.Two vertices of a rhombus are at the foci of the ellipse 9x2 + 25y2 - 225 = 0, the other two are at the vertices of the ellipse on its minor axis. Calculate the area of the rhombus.
Solution:
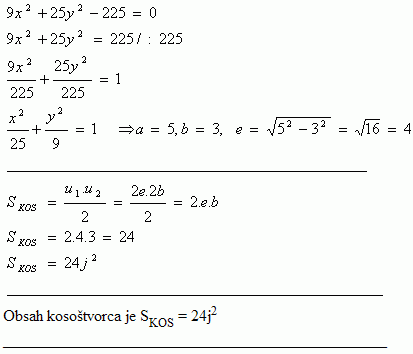
Content of a rhombus
12.Determine the equation of the ellipse in center form with S [0;0] that passes through points A [8;3] and [6;4]
Solution:
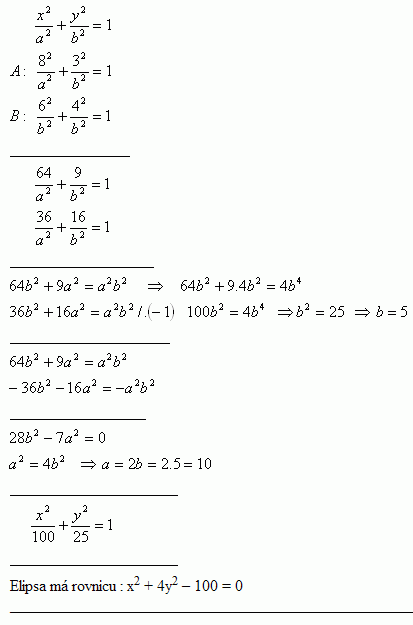
The ellipse has the equation
13.Write the equation of the line that passes through point A [1;5] and the center of the ellipse 4x2 + 9y2 - 24x + 36y +36 = 0
Solution:
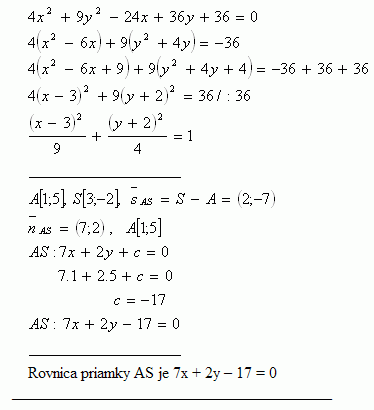
Equation of a straight line
14.Into the ellipse 2x2 + y2 – 4x + 4y – 108 = 0 a square ABCD is inscribed. Find its perimeter and area.
Solution:
2x2 + y2 – 4x + 4y – 108 = 0
(2x2-4x) + (y2+4y) = 108
2(x2-2x+1) +(y2+4y+4) = 108+2+4
2(x-1)2 + ( y+2)2 =114 y = x
2(x2- 2x+1 ) + ( x2 +4x +4 ) = 114
3x2 – 108 = 0
3x2 = 108
x2 = 36
x = ±6
X = (1+x ; -2+x )
A [7; 4 ] B [-5; 4] C [ -5; -8] D [ 7 ; -8]
a = | AB| = |BC| = |CD| = |DA| = 12
a = 12 j
P = 4a , S = a2
P = 4·12 S = 122
P = 48 j S = 144 j2
The perimeter of the square is P = 48 j, its area is S = 144 j2.
15.Find the distance from the center of the ellipse 4x2 + 9y2 -16x + 36y + 16 = 0 to the line 5x - 12y + 5 = 0
Solution:
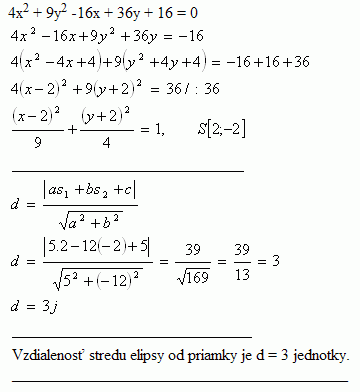
The distance between the center of the ellipse and the line is d = 3 units.
16.On an ellipse with center S [3; 2], semi-axis b = 4, eccentricity e = 3 find the point whose y-coordinate is y = 2
Solution:
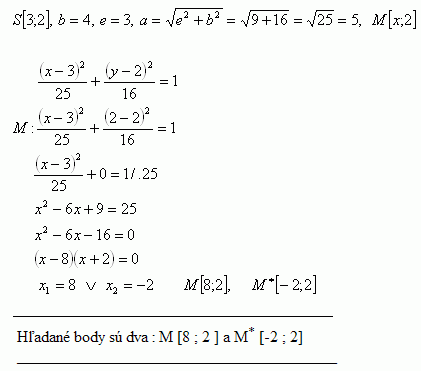
There are two points to look for
17.Given triangle ΔABC with side lengths |AB| = 6, |AC| = 7, |BC| = 3. Write the equation of the ellipse that has its foci at two vertices of the triangle and passes through the third vertex.
Solution:

The ellipse has the equation
18.Determine and examine the conic that passes through points: K[0;0], L[8;0], M[0;6], N[8;6]. O[2;-2]
Solution:
Ax2 + By2 + Cx + Dy + E = 0
Solve the system of equations:
K: 0 + 0 + 0 + E = 0
L: 64A + 0 + 8C + 0 + E = 0
M: 0 + 36B + 0 + 6D + E = 0
N: 64A + 36B + 8C + 6D + E = 0
O: 4A + 4B + 2C – 2D + E = 0
A = 4, B = 3, C = -32, D = -18, E = 0
4x2 + 3y2 – 32x -18y = 0 .
The conic is an ellipse with equation 4x2 + 3y2 -32x -18y = 0
19.Compute the length of the chord that the line 2x + y – 14 = 0 cuts from the ellipse 4x2 + y2 -100 = 0
Solution:
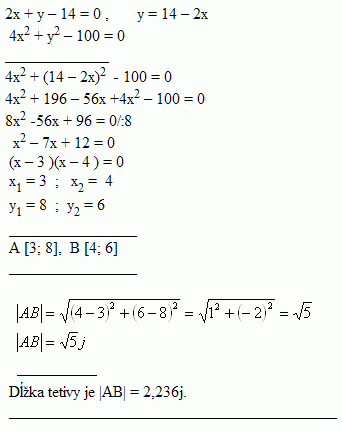
The length of the bowstring is
20.Write the equation of an ellipse when a given point M [3;-1] is the endpoint of the minor semi-axis b, the foci lie on the line p: y + 6 = 0. For the eccentricity of the ellipse it holds:
Solution:
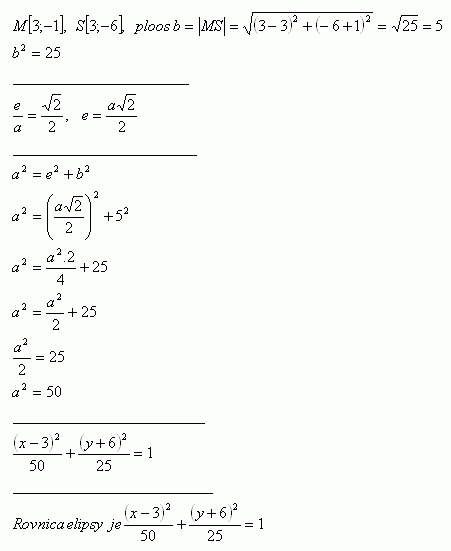
The ellipse has the equation
21.Determine the center and semi-axes of the hyperbola 9x2 -16y2 -36x + 32y – 124 = 0. Also determine the equations of its asymptotes.
Solution:
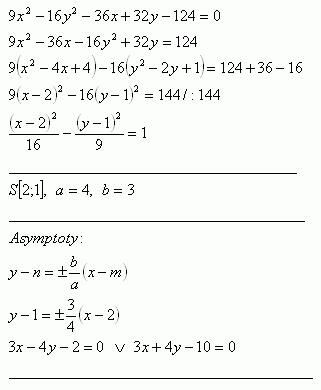
22.Write the equation of the hyperbola if its foci are F1 [-10;2], F2 [16;2]. Real axis 2a = 24
Solution:
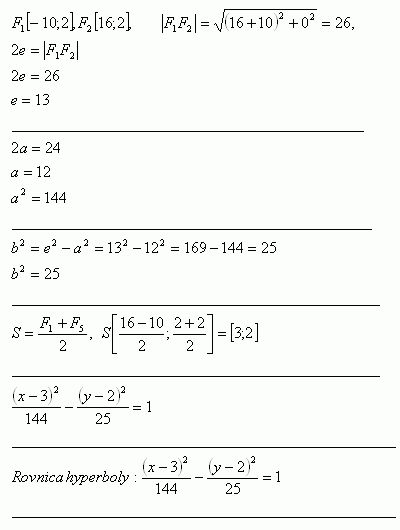
The hyberbola has the equation
23.Write the equation of the line on which lies the axis of symmetry of the segment that connects the centers of the hyperbolas x2 – y2 + 6x - 8y – 107 = 0 and 16x2 -9y2 -160x + 36y +220 = 0
Solution:
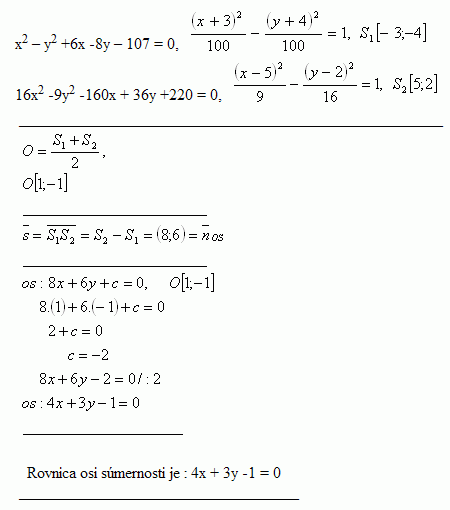
Equation of axis of symmetry
24.Given the hyperbola 16x2 – 25y2 – 400 = 0. Write: a) equations of the asymptotes, b) the angle between the asymptotes
Solution:
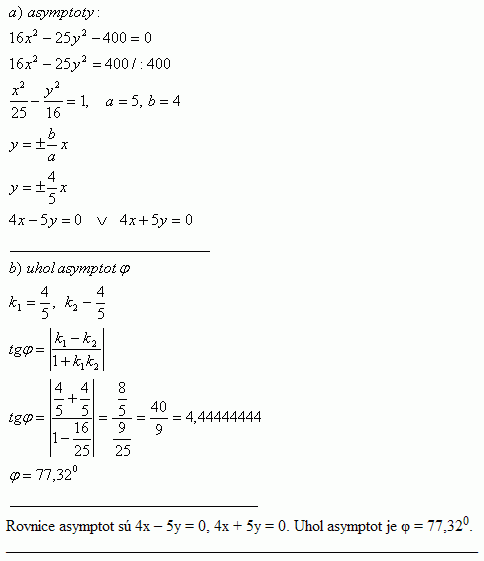
25.Write the central equation of the hyperbola that passes through the points:
Solution:
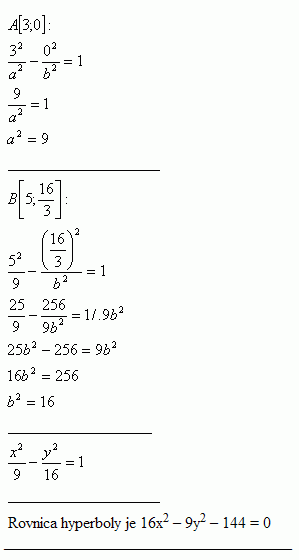
Hyperbola equation is
26.Prove that the product of distances from any point M of the hyperbola 2x2 – y2 – 2 = 0 to its asymptotes is constant and equals 2 : 3
Solution:

The claim has been proven
27.Find the set of all points in the plane that have a constant ratio of distances to point M [-5;0] and to the line p: 5x + 16 = 0 equal to 5 : 4
Solution:
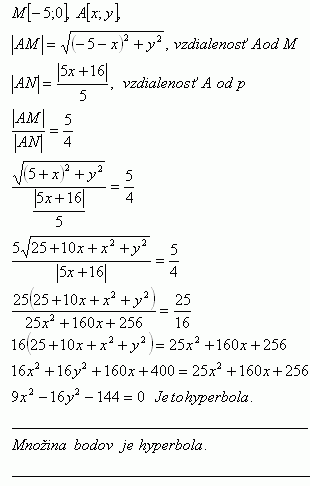
Sets of points is hyperbola
28.Write the equation of the hyperbola whose vertices are at the foci of the ellipse x2 + 2y2 – 18 = 0 and whose foci are at the vertices of that ellipse
Solution:
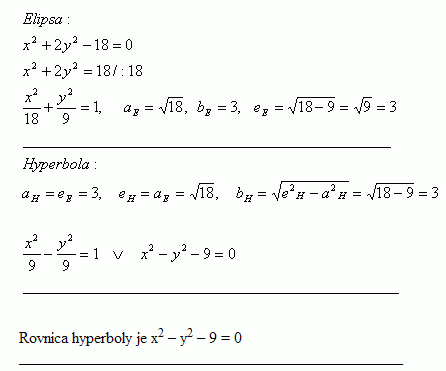
Hyperbola equation
29.Write the equation of the line that passes through point M [5 ; 4] and the vertex V of the parabola y2 - 6x + 10y + 31 = 0
Solution:
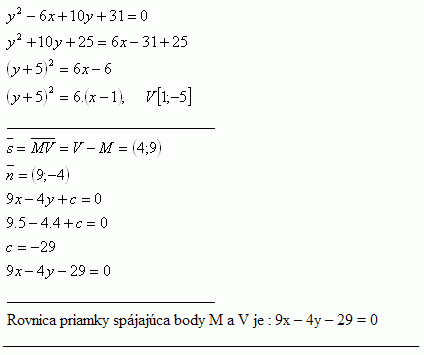
Equation of a line connecting points
30.Given parabolas x2 - 8x - 3y + 10 = 0 and x2 + 14x - 4y + 61 = 0. Compute the distance between their vertices |V1V2|
Solution:
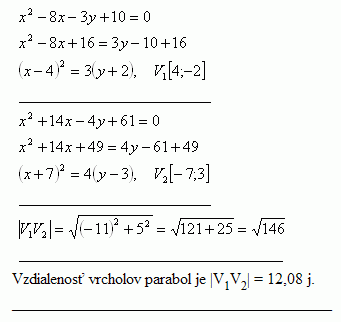
Distance between the vertices of a parabols
31.Write the equation of a parabola (opening parallel to the y-axis) that passes through points K[1;2], L[3;1], M[7;5].
Solution:
x2 + Ax + By + C = 0
K: 1 + A + 2B + C = 0
L: 9 + 3A + B + C = 0
M: 49 + 7A + 5B + C = 0
A = -6, B = -4, C = 13,
x2 – 6x – 4y + 13 = 0
x2 – 6x – 4y + 13 = 0
x2 – 6x + 9 = 4y - 13 + 9
(x – 3)2 = 4y – 4
(x – 3)2 = 4·(y – 1)
The equation of the parabola is (x – 3)2 = 4(y – 1).
32.On what curve lie the points in the plane whose sum of distances from the x-axis and from point B[8;0] is constant and equal to 24.
Solution:
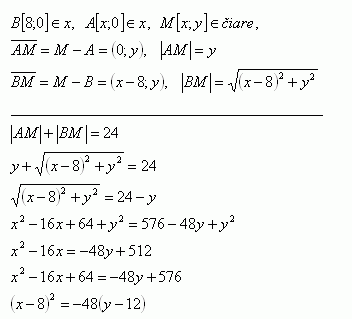
The curve is the parabola (x-8)2 = -48(y-12), opening in the negative y-direction.
33.The parabola has equation p: y2 = 8x. Compute the coordinates of the square ABCD if A coincides with the vertex of the parabola, C lies on the x-axis and points B, D lie on the parabola.
Solution:
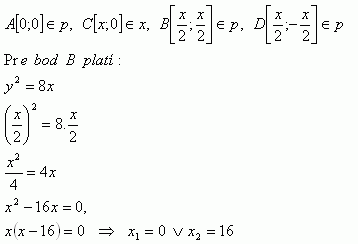
The vertices of the square are: A[0;0], B[8;8], C[16;0], D[8;-8]
34.Determine the side length of an equilateral triangle ΔABC inscribed in the parabola y2 = 5x
Solution:
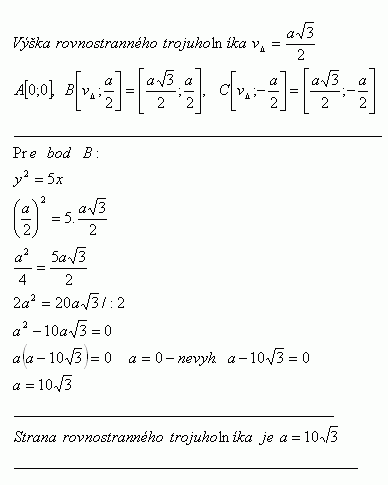
Side of an equilateral triangle is
35.Compute the length of the chord that the parabola y2 = 2x cuts from the ellipse 4x2 + 9y2 – 400 = 0.
Solution:
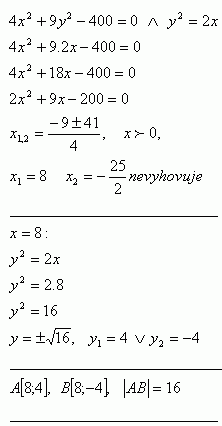
The length of the chord is |AB| = 16 j.
36.Determine the positions of points A, B, C, D at which the ellipse x2 + 2y2 -18 = 0 intersects the hyperbola x2 – y2 – 9 = 0.
Solution:
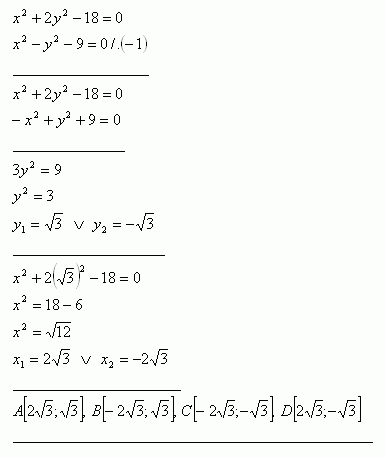
37.On the ellipse find the points that are at distance r = 14 from the right focus (e > 0). Ellipse equation:
Solution:
Ellipse : a2 = 100, b2 = 36, e2 = a2 – b2 = 100 – 36 = 64, e = 8
Circle : Center = F2[8;0], r = 14
( x – 8 )2 + y2 = 142
x2 – 16x + 64 + y2 – 196 = 0 ⇒ y2 = -x2 + 16x + 132
Ellipse :
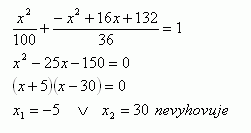
The sought points:
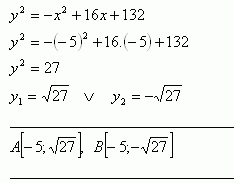
38.Compute the perimeter of rectangle ABCD whose vertices are intersections of the circle k: x2 + y2 = 50 and the hyperbola h: x2 – y2 = 48.
Solution:
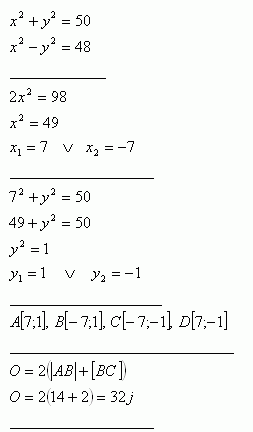
The perimeter of the rectangle is P = 32 j