The physical meaning of derivation
1. What is the physical meaning of the derivative?
Solution:
- The instantaneous velocity at time t0 is the first derivative of displacement with respect to time:
v(t0) = s‘(t0).
- The instantaneous acceleration at time t0 is the first derivative of velocity with respect to time:
a(t0) = v‘(t0)
Example:
Find the instantaneous velocity and instantaneous acceleration of a motion at time t, whose displacement is given by the relation:
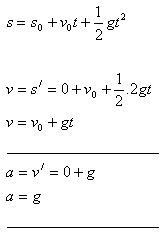
2.A stone thrown vertically upward from a height h = 10 m has initial velocity v0 = 20 m·s-1. What will be the stone's velocity at time t = 1.5 s? After what time will it reach its maximum height? What height will it reach? (g = 10 m·s-2)
Solution:
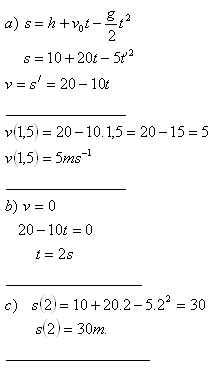
The stone's velocity at time t = 1.5 s is v = 5 m·s-1. It reaches the maximum height of 30 m after 2 seconds.
3.An object slides down an inclined plane 50 m long in 10 s. What is its final velocity, assuming that the displacement is a quadratic function of time and that the initial velocity is zero?
Solution:
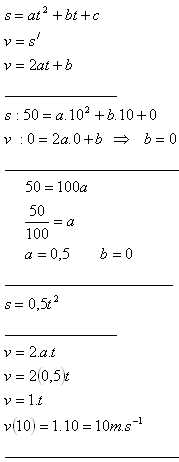
The final velocity of the object is v = 10 m·s-1.
4.A fast train traveling at 90 km·h-1 must brake uniformly so that it stops over a distance of 1 km. After what time will it stop?
Determine its velocity 10 seconds after it began braking.
Solution:
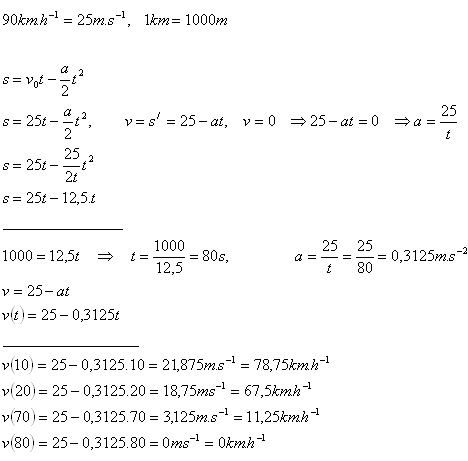
The train stops after 80 s.
5.Find how quickly altitude changes with air pressure.
The formula giving the altitude above Earth's surface as a function of air pressure. (p0 is the standard air pressure at sea level):
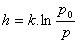
Solution:
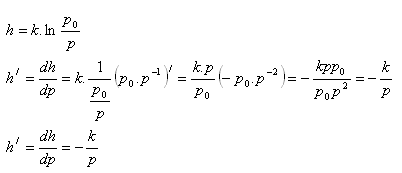
6.Determine the rate of change of vapor pressure (p) with respect to absolute temperature (T), if:
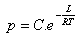
(C, L, R are constants)
Solution:
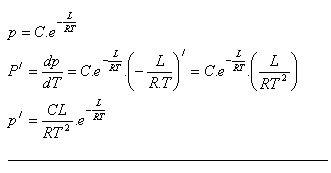
7.The amount of electric charge Q passing through a conductor changes with time according to Q = 3t2 + 2t + 2. ([Q] = C, [t] = s)
Calculate the instantaneous current i at time t = 1 s. Also determine when the current i = 20 A.
Solution:
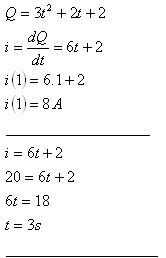
At time t = 1 s, i = 8 A. The current i = 20 A occurs at t = 3 seconds.
8.In an inductive coil the current is i = 15·sin5(3t), [i] = A, [t] = s, [L] = 0.03 H. Calculate the induced electromotive force at time t = 2π/9 s according to the formula:
Solution:

9.An object moves along a line and its displacement from equilibrium is given by: y = 2cos2πt - 3sin2πt. Find its velocity at time t = 1 s and the maximum displacement from equilibrium. (y is in cm)
Solution:
Velocity :
y = 2cos2πt – 3sin2πt
v = y‘ = 4π·(-sin2πt) - 6π·(cos2πt)
v = y‘ = -2π·(2sin2πt + 3cos2πt)
v(1) = y′(1) = -2π·(2sin2π + 3cos2π)
v(1) = y′(1) = -2π·(0 + 3·1)
v(1) = –6π [cm·s-1]
Maximum displacement :
v = 0
-2π·(2sin2πt + 3cos2πt) = 0 /:(-2π)
2sin2πt + 3cos2πt = 0 /:cos2πt
2·tan2πt + 3 = 0
tan2πt = –1.5
2πt = 124°
ymax = 2cos124° - 3sin124° = -1.1183 - 2.4871 = –3.6054
ymax = -3.6054 cm.
10.The power of a battery with electromotive force E and internal resistance Ri is: P = E·I – Ri·I2. At what current does the battery deliver maximum power? Determine that power.
Solution:
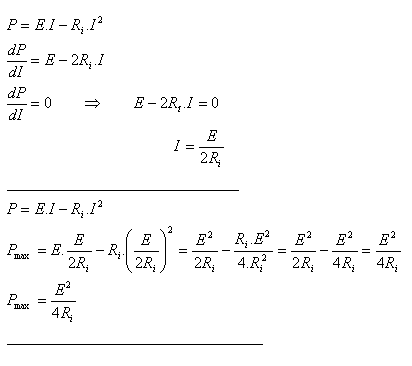
11.For the displacement of harmonic motion s = A·sin(ω·t). Derive the formulas for the velocity and acceleration of harmonic motion.
Solution:
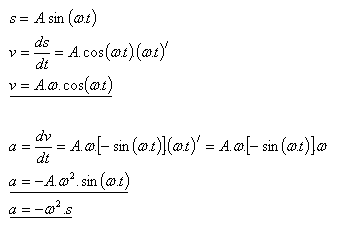
The formula for the velocity of harmonic motion is v = A·ω·cos(ω·t), and for the acceleration a = –ω2·s.
12.The relationship between amount and mass in some chemical reactions is given by
x = A·(1 – e–kt). (A, k are constants).
Calculate the rate of this reaction.
Solution:
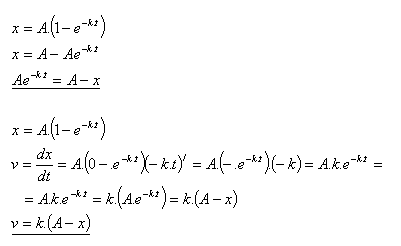
The reaction rate is given by v = k·(A – x).
13.A flywheel is rotating, is slowed down, and its motion is described by the equation
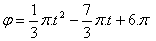
Write the equation for the angular velocity and determine after what time the motion becomes uniform rotation with angular velocity ω = π.
Solution:
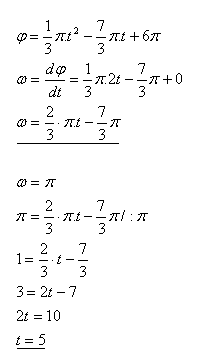
The angular velocity ω = π is reached after t = 5 seconds.
14.The piston moves back and forth according to s = –1.5 t3 + 9 t2 (cm). Calculate the maximum distance the piston reaches in 4 seconds. Also determine the velocities v0, v1, ... v6.
Solution:
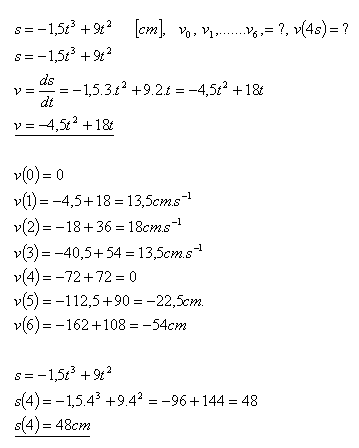
The piston reaches 48 cm after 4 seconds.
15.For a moving body the displacement is given by s = t2 + 3t – 5 (m) and at time t = 0 its velocity was zero. Determine the displacement, velocity and acceleration at time t = 5 s. Also determine its kinetic energy if its mass is 8 kg.
Solution:
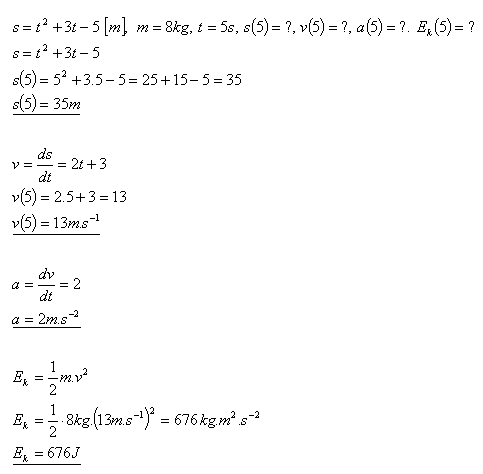
The kinetic energy of the body at the fifth second is Ek = 676 J.
16.An object moves along the path s = t2 – t3/3 + 3t + 8 (m). Calculate
- a.) after what time it stops
- b.) what its acceleration will be at time t = 0.5 s
- c.) what distance the object travels until it stops
Solution:
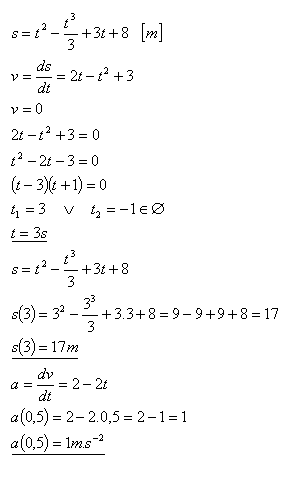
- The object stops after 3 seconds and travels 17 meters.
- Its deceleration at time 0.5 s will be 1 m·s–2.
17.The amount of electric charge passing through a conductor changes according to Q = 2·t·e–t. Find the time when the current intensity will be zero.
Solution:
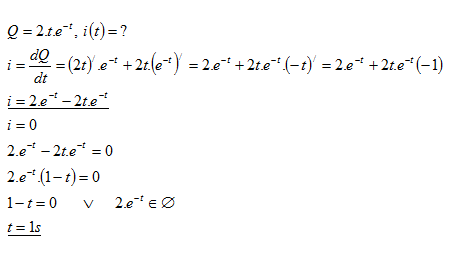
The current intensity will be zero at time t = 1 second.
18.Verify that the given function describing the current of a discharging capacitor satisfies the differential equation:
Solution:
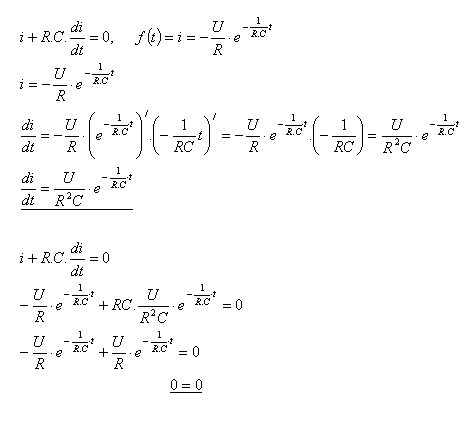
The function satisfies the given differential equation.