Equation of a plane
1. In what way is a plane in space determined?
Solution:
A plane in space is determined by three distinct points A, B, C that do not lie on the same line.

2.Write the general equation of the plane that contains point A [-1;5;0]. Does the plane ρ pass through the origin? The normal vector of the plane is
Solution:
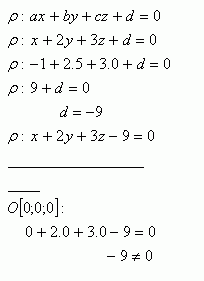
The plane x + 2y + 3z - 9 = 0 does not pass through the origin.
3. In plane ρ lie three points A[2 ; -4; 5], B[3; -1;4], C[0; -10; 7]. Write the parametric representation of this plane.
Solution:
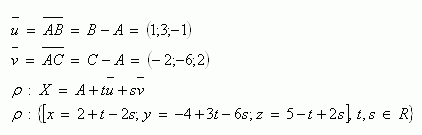
4.The plane ρ is given by parametric equations. Convert them to the general equation of the plane.
Solution:
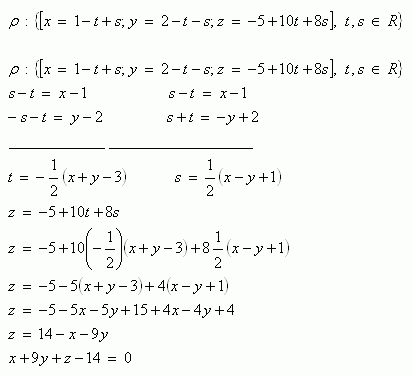
The plane equation in general form is ρ: x + 9y + z - 14 = 0
5. Write the equation of plane σ that passes through point A [3;4;-5] and is parallel to the vectors
Solution:

6.Write the equation of the plane that passes through points A [2;-4;5], B [3;-1;4], C [0;1;6]
Solution:

The equation of the plane is 8x + y + 11z – 67 = 0
7. Write the equation of the plane given by two parallel lines:
Solution:

The equation of the plane is ρ: 2x + y - 1 = 0
8.Write the general equation of the plane τ that is parallel to the x-axis and passes through points A[-2;-1;-3], B [2;3;0]
Solution:

The equation of the plane is τ: 3y – 4z - 9 = 0
9. Write the equation of plane π that passes through point M[-4;0;4] and intercepts on the coordinate axes segments p = 4, q = 3.
Solution:
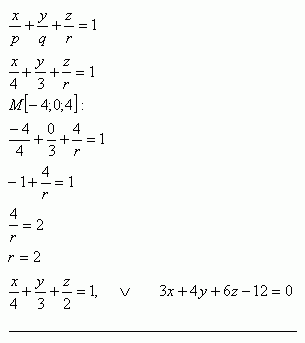
The equation of plane π: 3x + 4y + 6z - 12 = 0
10. Given the plane ρ : 2x - 2y + z - 6 = 0. Calculate the angles between its normal and the x, y, z coordinate axes.
Solution:
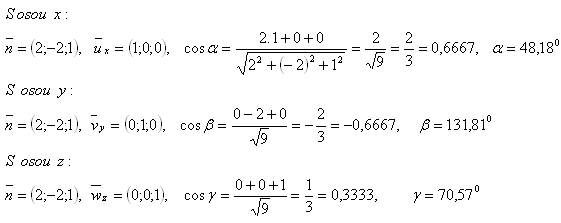
The angles of the normal with the coordinate axes are: α = 48.180, β = 131.810, γ = 70.570
11.Determine whether point A [22;2;–5] lies in the plane
Solution:
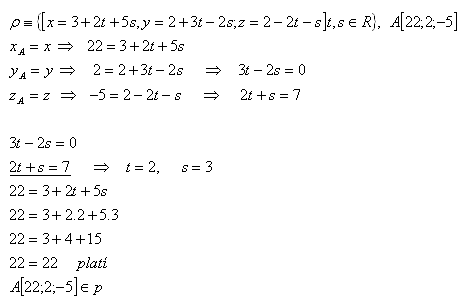
Point A lies in plane ρ.
12.Determine the coordinate "x" of point M [x;1,2] so that point M lies in the plane
Solution:
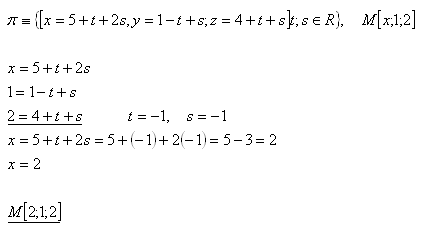
The sought coordinate of point M is x = 2. Point M is [2;1;2].
13.Write the general equation of the plane that passes through point A and is perpendicular to segment AB, given:
Solution:
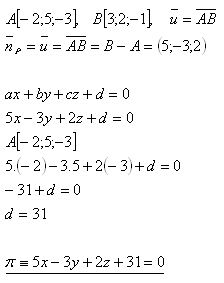
The equation of the plane is π : 5x - 3y + 2z + 31 = 0
14.Write the general equation of the plane τ that intercepts on the coordinate axes segments p = 2, q = 1, r = 5.
Solution:
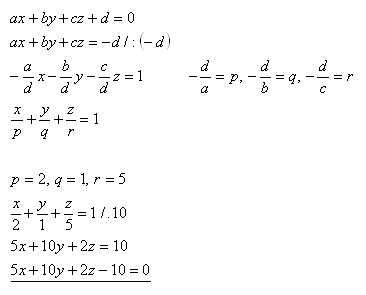
The equation of the plane is τ : 5x + 10y + 2z – 10 = 0
15.Write the equation of plane π that passes through point M and is perpendicular to line p. Solve for the given data:
Solution:
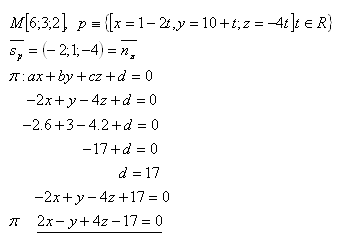
The equation of the plane is π : 2x – y + 4z – 17 = 0
16.Show that points A, B, C, D lie in a single plane. Solve for:
Solution:
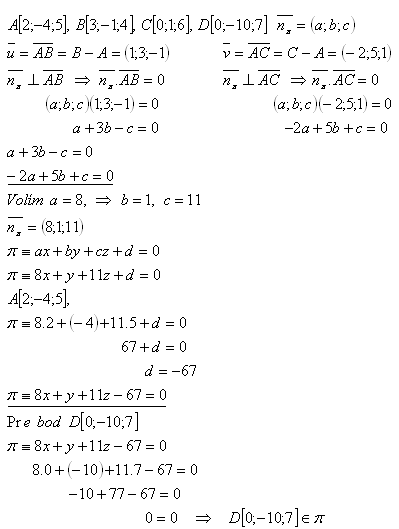
Point D[0;-10;7] lies in plane π. All points A, B, C, D lie in plane π.
17.Given three spheres π, τ, ρ. Write the general equation of the plane χ that passes through the centers of these spheres. It holds that:
Solution:
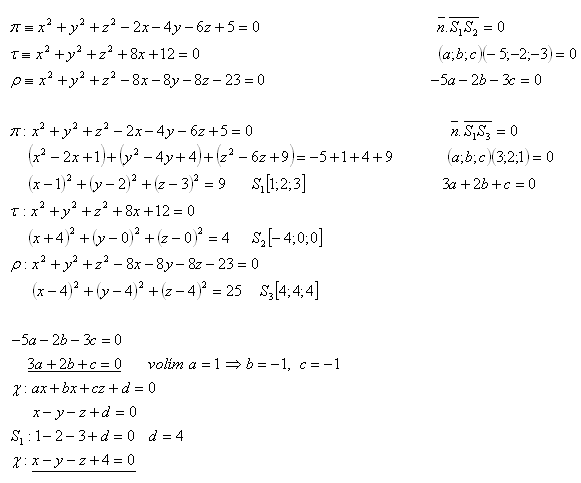
The equation of the plane is: x – y – z + 4 = 0
18.Write the general equation of plane π that passes through the points
Solution:
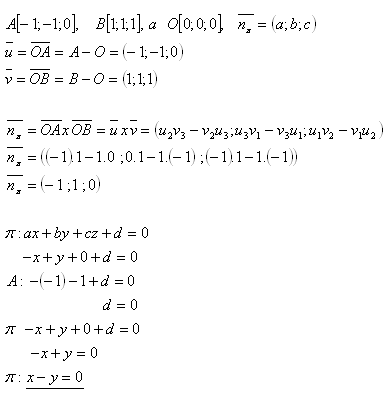
The equation of the plane is π : x – y = 0
19.Convert the parametric form of plane μ to the general form, given
Solution:
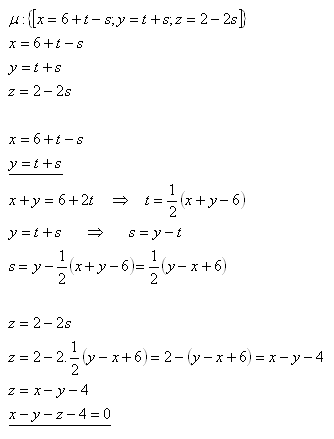
The equation of plane μ in general form is μ: x – y – z – 4 = 0
20.For which value of the parameter "m" from the set R does point M[0;6;m] lie in the plane
Solution:
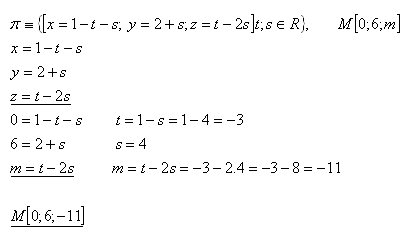
The parameter "m" is m = –11. Point M [0;6;–11].